|
List Of Things Named After Josiah W. Gibbs
{{Short description, none Things named after American scientist Josiah Willard Gibbs: *Gibbs algorithm * Gibbs canonical ensemble *Gibbs distribution * Gibbs elasticity * Gibbs ensemble *Gibbs entropy *Gibbs free energy * Gibbs H-theorem *Gibbs' inequality *Gibbs isotherm * Gibbs lemma *Gibbs measure **Gibbs random field * Gibbs phase rule *Gibbs paradox *Gibbs phenomenon *Gibbs sampling *Gibbs state * Gibbs's thermodynamic surface * Gibbs vector * Gibbs–Appell equation of motion *Gibbs–Donnan effect *Gibbs–Duhem equation *Gibbs–Helmholtz equation *Gibbs–Marangoni effect * Gibbs–Thomson effect *Gibbs–Thomson equation * Gibbs–Wulff theorem * Massieu–Gibbs function Heavenly bodies *2937 Gibbs (asteroid) *Gibbs (crater) Other honours * Gibbs Society of Biological Thermodynamics *Josiah Willard Gibbs Lectureship *Willard Gibbs Award gibbs Gibbs or GIBBS is a surname and acronym. It may refer to: People * Gibbs (surname) Places * Gibbs (crater), on the Moon * Gibb ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Josiah Willard Gibbs
Josiah Willard Gibbs (; February 11, 1839 – April 28, 1903) was an American mechanical engineer and scientist who made fundamental theoretical contributions to physics, chemistry, and mathematics. His work on the applications of thermodynamics was instrumental in transforming physical chemistry into a rigorous deductive science. Together with James Clerk Maxwell and Ludwig Boltzmann, he created statistical mechanics (a term that he coined), explaining the laws of thermodynamics as consequences of the statistical properties of ensembles of the possible states of a physical system composed of many particles. Gibbs also worked on the application of Maxwell's equations to problems in physical optics. As a mathematician, he created modern vector calculus (independently of the British scientist Oliver Heaviside, who carried out similar work during the same period) and described the Gibbs phenomenon in the theory of Fourier analysis. In 1863, Yale University awarded Gibbs the firs ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
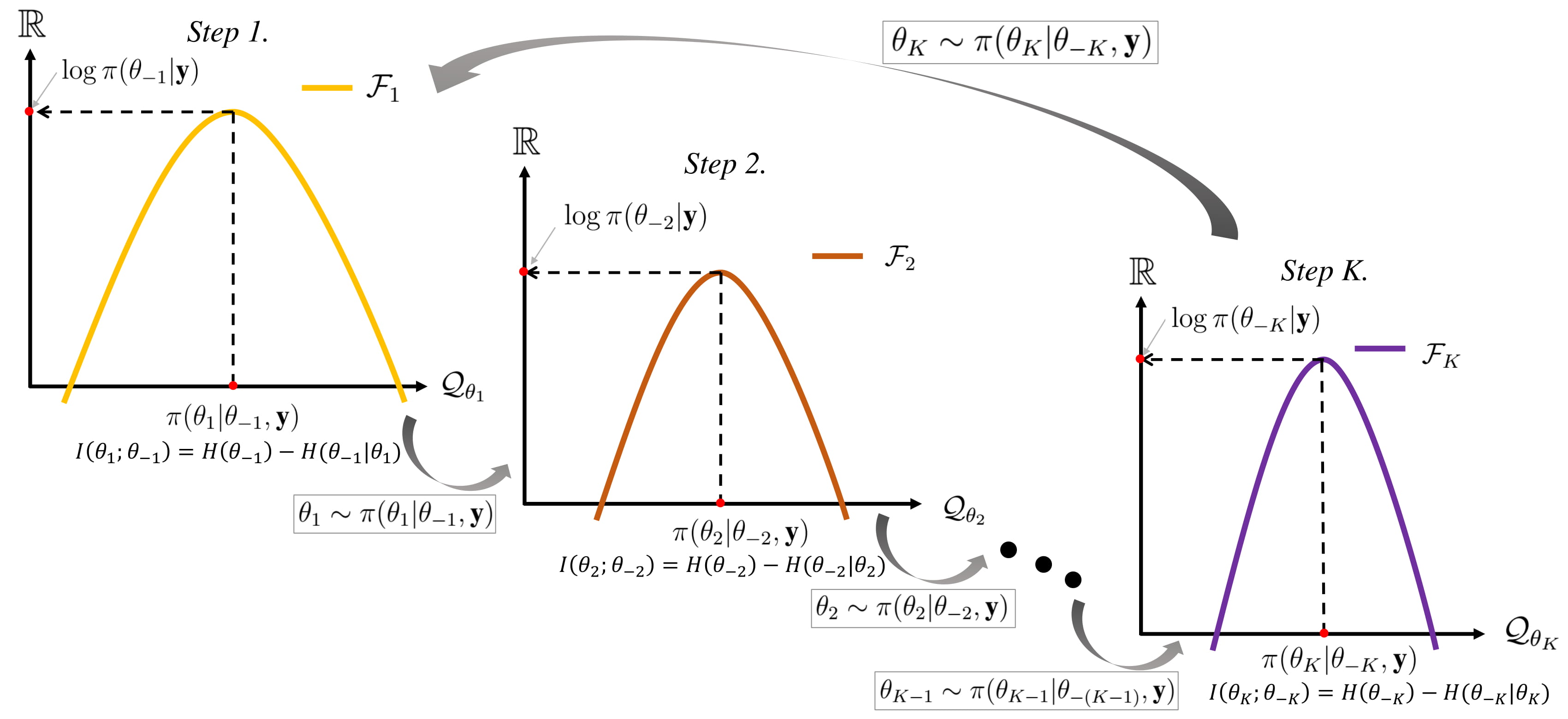
Gibbs Sampling
In statistics, Gibbs sampling or a Gibbs sampler is a Markov chain Monte Carlo (MCMC) algorithm for sampling from a specified multivariate distribution, multivariate probability distribution when direct sampling from the joint distribution is difficult, but sampling from the Conditional probability distribution, conditional distribution is more practical. This sequence can be used to approximate the joint distribution (e.g., to generate a histogram of the distribution); to approximate the marginal distribution of one of the variables, or some subset of the variables (for example, the unknown parameters or latent variables); or to compute an integral (such as the expected value of one of the variables). Typically, some of the variables correspond to observations whose values are known, and hence do not need to be sampled. Gibbs sampling is commonly used as a means of statistical inference, especially Bayesian inference. It is a randomized algorithm (i.e. an algorithm that makes ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
2937 Gibbs
2937 Gibbs, provisional designation , is a stony Phocaea asteroid and Mars-crosser from the inner regions of the asteroid belt, approximately 6 kilometers in diameter. It was discovered on 14 June 1980, by American astronomer Edward Bowell at Lowell's Anderson Mesa Station near Flagstaff, Arizona. The asteroid was named after American scientist Josiah Willard Gibbs. Orbit and classification ''Gibbs'' is a Mars-crossing asteroid, as it crosses the orbit of Mars at 1.666 AU. It is also an eccentric member of the Phocaea family, a large asteroid family of stony asteroids in the inner main-belt. ''Gibbs'' orbits the Sun at a distance of 1.6–3.0 AU once every 3 years and 6 months (1,290 days). Its orbit has an eccentricity of 0.30 and an inclination of 22 ° with respect to the ecliptic. The asteroid's observation arc begins with its official discovery observation at Anderson Mesa. No prior identifications were made and no precoveries taken. Physical characteristic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Massieu Function
In thermodynamics, the Massieu function (sometimes called Massieu–Gibbs function, Massieu potential, or Gibbs function, or characteristic (state) function in its original terminology), symbol ( Psi), is defined by the following relation: : \Psi = \Psi \big( X_1, \dots, X_i, Y_, \dots Y_r \big) \, where for every system with degree of freedom one may choose variables, e.g. \big( X_1, \dots, X_i, Y_, \dots Y_r \big) , to define a coordinate system, where and are extensive and intensive variables, respectively, and where at least one extensive variable must be within this set in order to define the size of the system. The -th variable, , is then called the Massieu function.Inden, Gerhard. (2008). �Introduction to Thermodynamics��, ''Materials Issues for Generation IV Systems'', pgs. 73–112. Springer The Massieu function was introduced in the 1869 paper "On the Characteristic Functions of Various Fluids" by French engineer François Massieu (1832-1896). The ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wulff Construction
The Wulff construction is a method to determine the equilibrium shape of a droplet or crystal of fixed volume inside a separate phase (usually its saturated solution or vapor). Energy minimization arguments are used to show that certain crystal planes are preferred over others, giving the crystal its shape. It is of fundamental importance in a number of areas ranging from the shape of nanoparticles and precipitates to nucleation. It also has more applied relevance in areas such as the shapes of active particles in heterogeneous catalysis. Theory In 1878 Josiah Willard Gibbs proposed that a droplet or crystal will arrange itself such that its surface Gibbs free energy is minimized by assuming a shape of low surface energy. He defined the quantity :\Delta G_i= \sum_\gamma_j O_j~ Here \gamma _j represents the surface (Gibbs free) energy per unit area of the jth crystal face and O_j is the area of said face. \Delta G_i represents the difference in energy between a real crystal c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gibbs–Thomson Equation
The Gibbs–Thomson effect, in common physics usage, refers to variations in vapor pressure or chemical potential across a curved surface or interface. The existence of a positive interfacial energy will increase the energy required to form small particles with high curvature, and these particles will exhibit an increased vapor pressure. See Ostwald–Freundlich equation. More specifically, the Gibbs–Thomson effect refers to the observation that small crystals that are in equilibrium with their liquid, melt at a lower temperature than large crystals. In cases of confined geometry, such as liquids contained within porous media, this leads to a depression in the freezing point / melting point that is inversely proportional to the pore size, as given by the Gibbs–Thomson equation. Introduction The technique is closely related to using gas adsorption to measure pore sizes, but uses the Gibbs–Thomson equation rather than the Kelvin equation. They are both particular cases of the G ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gibbs–Marangoni Effect
The Marangoni effect (also called the Gibbs–Marangoni effect) is the mass transfer along an interface between two phases due to a gradient of the surface tension. In the case of temperature dependence, this phenomenon may be called thermo-capillary convection or Bénard–Marangoni convection. History This phenomenon was first identified in the so-called "tears of wine" by physicist James Thomson (Lord Kelvin's brother) in 1855. The general effect is named after Italian physicist Carlo Marangoni, who studied it for his doctoral dissertation at the University of Pavia and published his results in 1865. A complete theoretical treatment of the subject was given by J. Willard Gibbs in his work ''On the Equilibrium of Heterogeneous Substances'' (1875–1878). Mechanism Since a liquid with a high surface tension pulls more strongly on the surrounding liquid than one with a low surface tension, the presence of a gradient in surface tension will naturally cause the liquid to flow awa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gibbs–Helmholtz Equation
The Gibbs–Helmholtz equation is a thermodynamic equation used to calculate changes in the Gibbs free energy of a system as a function of temperature. It was originally presented in an 1882 paper entitled " Die Thermodynamik chemischer Vorgänge" by Hermann von Helmholtz. It describes how the Gibbs free energy, which was presented originally by Josiah Willard Gibbs, varies with temperature. It was derived by Helmholtz first, and Gibbs derived it only 6 years later. The attribution to Gibbs goes back to Wilhelm Ostwald, who first translated Gibbs' monograph into German and promoted it in Europe. The equation is:Physical chemistry, P. W. Atkins, Oxford University Press, 1978, where ''H'' is the enthalpy, ''T'' the absolute temperature and ''G'' the Gibbs free energy of the system, all at constant pressure ''p''. The equation states that the change in the ''G/T'' ratio at constant pressure as a result of an infinitesimally small change in temperature is a factor ''H/T''2. S ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gibbs–Duhem Equation
In thermodynamics, the Gibbs–Duhem equation describes the relationship between changes in chemical potential for components in a thermodynamic system: \sum_^I N_i \mathrm\mu_i = - S \mathrmT + V \mathrmp where N_i is the number of moles of component i, \mathrm\mu_i the infinitesimal increase in chemical potential for this component, S the entropy, T the absolute temperature, V volume and p the pressure. I is the number of different components in the system. This equation shows that in thermodynamics intensive properties are not independent but related, making it a mathematical statement of the state postulate. When pressure and temperature are variable, only I-1 of I components have independent values for chemical potential and Gibbs' phase rule follows. The Gibbs−Duhem equation applies to homogeneous thermodynamic systems. It does not apply to inhomogeneous systems such as small thermodynamic systems, systems subject to long-range forces like electricity and gravity, or ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gibbs–Donnan Effect
The Gibbs–Donnan effect (also known as the Donnan's effect, Donnan law, Donnan equilibrium, or Gibbs–Donnan equilibrium) is a name for the behaviour of charged particles near a semi-permeable membrane that sometimes fail to distribute evenly across the two sides of the membrane. The usual cause is the presence of a different charged substance that is unable to pass through the membrane and thus creates an uneven electrical charge Electricity is the set of physical phenomena associated with the presence and motion of matter possessing an electric charge. Electricity is related to magnetism, both being part of the phenomenon of electromagnetism, as described by Maxwel .... For example, the large anionic proteins in blood plasma are not permeable to capillary walls. Because small cations are attracted, but are not bound to the proteins, small anions will cross capillary walls away from the anionic proteins more readily than small cations. Thus, some ionic species can p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |