|
List Of Things Named After Isaac Newton
This is a list of things named after Sir Isaac Newton Sir Isaac Newton () was an English polymath active as a mathematician, physicist, astronomer, alchemist, theologian, and author. Newton was a key figure in the Scientific Revolution and the Enlightenment that followed. His book (''Mathe .... Science and mathematics * Newtonianism, the philosophical principle of applying Newton's methods in a variety of fields Mathematics Physics Places Schools Artwork Other See also * Newtonian (other) {{Isaac Newton Newton Newton Named after ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sir Isaac Newton
Sir Isaac Newton () was an English polymath active as a mathematician, physicist, astronomer, alchemist, theologian, and author. Newton was a key figure in the Scientific Revolution and the Enlightenment that followed. His book (''Mathematical Principles of Natural Philosophy''), first published in 1687, achieved the first great unification in physics and established classical mechanics. Newton also made seminal contributions to optics, and shares credit with German mathematician Gottfried Wilhelm Leibniz for formulating infinitesimal calculus, though he developed calculus years before Leibniz. Newton contributed to and refined the scientific method, and his work is considered the most influential in bringing forth modern science. In the , Newton formulated the laws of motion and universal gravitation that formed the dominant scientific viewpoint for centuries until it was superseded by the theory of relativity. He used his mathematical description of gravity to deriv ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Newton Polynomial
In the mathematical field of numerical analysis, a Newton polynomial, named after its inventor Isaac Newton, is an interpolation polynomial for a given set of data points. The Newton polynomial is sometimes called Newton's divided differences interpolation polynomial because the coefficients of the polynomial are calculated using Newton's divided differences method. Definition Given a set of ''k'' + 1 data points :(x_0, y_0),\ldots,(x_j, y_j),\ldots,(x_k, y_k) where no two ''x''''j'' are the same, the Newton interpolation polynomial is a linear combination of Newton basis polynomials :N(x) := \sum_^ a_ n_(x) with the Newton basis polynomials defined as :n_j(x) := \prod_^ (x - x_i) for ''j'' > 0 and n_0(x) \equiv 1. The coefficients are defined as :a_j := _0,\ldots,y_j/math> where _0,\ldots,y_j/math> are the divided differences defined as \begin \mathopen _k&:= y_k, && k \in \ \\ \mathopen _k,\ldots,y_&:= \frac, && k\in\,\ j\in\. \end Thus the Newton polynomi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Newton's Law Of Cooling
In the study of heat transfer, Newton's law of cooling is a physical law which states that the rate of heat loss of a body is directly proportional to the difference in the temperatures between the body and its environment. The law is frequently qualified to include the condition that the temperature difference is small and the nature of heat transfer mechanism remains the same. As such, it is equivalent to a statement that the heat transfer coefficient, which mediates between heat losses and temperature differences, is a constant. In heat conduction, Newton's law is generally followed as a consequence of Fourier's law. The thermal conductivity of most materials is only weakly dependent on temperature, so the constant heat transfer coefficient condition is generally met. In convective heat transfer, Newton's Law is followed for forced air or pumped fluid cooling, where the properties of the fluid do not vary strongly with temperature, but it is only approximately true for b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Newton–Euler Equations
In classical mechanics, the Newton–Euler equations describe the combined translational and rotational dynamics of a rigid body. Traditionally the Newton–Euler equations is the grouping together of Euler's two laws of motion for a rigid body into a single equation with 6 components, using column vectors and matrices. These laws relate the motion of the center of gravity of a rigid body with the sum of forces and torques (or synonymously moments) acting on the rigid body. Center of mass frame With respect to a coordinate frame whose origin coincides with the body's center of mass for τ(torque) and an inertial frame of reference for F(force), they can be expressed in matrix form as: : \left(\begin \\ \end\right) = \left(\begin m & 0 \\ 0 & _ \end\right) \left(\begin \mathbf a_ \\ \end\right) + \left(\begin 0 \\ \times _ \, \end\right), where :F = total force acting on the center of mass :''m'' = mass of the body :I3 = the 3×3 identity matrix :acm = accel ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Newton–Cartan Theory
Newton–Cartan theory (or geometrized Newtonian gravitation) is a geometrical re-formulation, as well as a generalization, of Newtonian gravity first introduced by Élie Cartan in 1923 and Kurt Friedrichs and later developed by G. Dautcourt, W. G. Dixon, P. Havas, H. Künzle, Andrzej Trautman, and others. In this re-formulation, the structural similarities between Newton's theory and Albert Einstein's general theory of relativity are readily seen, and it has been used by Cartan and Friedrichs to give a rigorous formulation of the way in which Newtonian gravity can be seen as a specific limit of general relativity, and by Jürgen Ehlers to extend this correspondence to specific solutions of general relativity. Classical spacetimes In Newton–Cartan theory, one starts with a smooth four-dimensional manifold M and defines ''two'' (degenerate) metrics. A ''temporal metric'' t_ with signature (1, 0, 0, 0), used to assign temporal lengths to vectors on M and a ''spatial metric'' h^ wi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
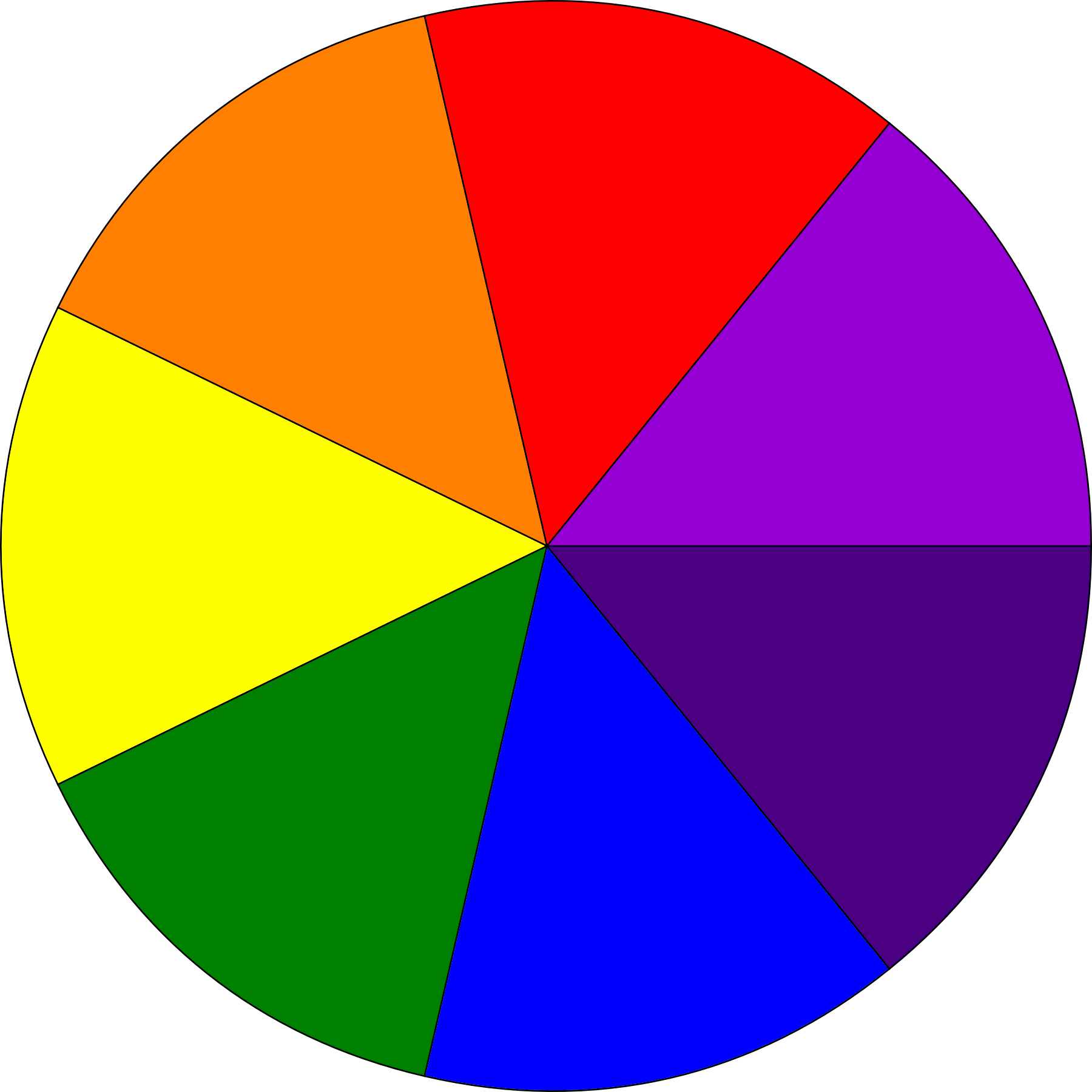
Newton Disc
The Newton disk, also known as the disappearing color disk, is a well-known physics experiment with a rotating disk with segments in different colors (usually Newton's primary colors: red, orange, yellow, green, blue, indigo, and violet, commonly known by the abbreviation ROYGBIV) appearing as white (or off-white or gray) when it is spun rapidly on its axis. This type of mix of light stimuli is called temporal optical mixing, a version of additive-averaging mixing. The concept that human visual perception cannot distinguish details of high-speed movements is popularly known as persistence of vision. The disk is named after Isaac Newton. Although he published a circular diagram with segments for the primary colors that he had discovered (i.e., a color wheel), it is unlikely that he ever used a spinning disk to demonstrate the principles of light. He referred to the mixture of colors painted on a spinning top as "dirty" and described several experiments supporting his theory. T ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Newton's Cradle
Newton's cradle is a device, usually made of metal, that demonstrates the principles of Momentum, conservation of momentum and conservation of energy in physics with swinging Sphere, spheres. When one sphere at the end is lifted and released, it strikes the stationary spheres, compressing them and thereby transmitting a pressure wave through the stationary spheres, which creates a force that pushes the last sphere upward. The last sphere swings back and strikes the stationary spheres, repeating the effect in the opposite direction. Newton's cradle demonstrates conservation of momentum and energy. The device is named after 17th-century English scientist Isaac Newton, Sir Isaac Newton and was designed by French scientist Edme Mariotte. It is also known as Newton's pendulum, Newton's balls, Newton's rocker or executive ball clicker (since the device makes a click each time the balls collide, which they do repeatedly in a steady rhythm). Operation When one of the balls at the e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Universal Gravitational Constant
The gravitational constant is an empirical physical constant involved in the calculation of gravitational effects in Sir Isaac Newton's law of universal gravitation and in Albert Einstein's theory of general relativity. It is also known as the universal gravitational constant, the Newtonian constant of gravitation, or the Cavendish gravitational constant, denoted by the capital letter . In Newton's law, it is the proportionality constant connecting the gravitational force between two bodies with the product of their masses and the inverse square of their distance. In the Einstein field equations, it quantifies the relation between the geometry of spacetime and the energy–momentum tensor (also referred to as the stress–energy tensor). The measured value of the constant is known with some certainty to four significant digits. In SI units, its value is approximately The modern notation of Newton's law involving was introduced in the 1890s by C. V. Boys. The firs ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Newton's Constant
The gravitational constant is an empirical physical constant involved in the calculation of gravitational effects in Sir Isaac Newton's law of universal gravitation and in Albert Einstein's theory of general relativity. It is also known as the universal gravitational constant, the Newtonian constant of gravitation, or the Cavendish gravitational constant, denoted by the capital letter . In Newton's law, it is the proportionality constant connecting the gravitational force between two bodies with the product of their masses and the inverse square of their distance. In the Einstein field equations, it quantifies the relation between the geometry of spacetime and the energy–momentum tensor (also referred to as the stress–energy tensor). The measured value of the constant is known with some certainty to four significant digits. In SI units, its value is approximately The modern notation of Newton's law involving was introduced in the 1890s by C. V. Boys. The first im ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Newton's Cannonball
Newton's cannonball was a thought experiment Isaac Newton used to hypothesize that the force of gravity was universal, and it was the key force for planetary motion. It appeared in his posthumously published 1728 work ''De mundi systemate'' (also published in English as '' A Treatise of the System of the World'').''De mundi systemate'' Isaac Newton, London: J. Tonson, J. Osborn, & T. Longman, 1728.''A Treatise of the System of the World'' Isaac Newton, London: printed for F. Fayram, 1728. Theory In this experiment from his book (pp. 5–8), Newton visualizes a stone being projected from the top ...[...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bucket Argument
Isaac Newton's rotating bucket argument (also known as Newton's bucket) is a thought experiment that was designed to demonstrate that true rotational motion cannot be defined as the relative rotation of the body with respect to the immediately surrounding bodies. It is one of five arguments from the "properties, causes, and effects" of "true motion and rest" that support his contention that, in general, true motion and rest cannot be defined as special instances of motion or rest relative to other bodies, but instead can be defined only by reference to absolute space. Alternatively, these experiments provide an operational definition of what is meant by " absolute rotation", and do not pretend to address the question of "rotation relative to ''what''?" General relativity dispenses with absolute space and with physics whose cause is external to the system, with the concept of geodesics of spacetime. Background These arguments, and a discussion of the distinctions between absolute ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Truncated Newton Method
The truncated Newton method, originated in a paper by Ron Dembo and Trond Steihaug,. Convergence results for this algorithm can be found in . also known as Hessian-free optimization, are a family of optimization algorithms designed for optimizing non-linear functions with large numbers of independent variables. A truncated Newton method consists of repeated application of an iterative optimization algorithm to approximately solve Newton's equations, to determine an update to the function's parameters. The inner solver is ''truncated'', i.e., run for only a limited number of iterations. It follows that, for truncated Newton methods to work, the inner solver needs to produce a good approximation in a finite number of iterations; conjugate gradient has been suggested and evaluated as a candidate inner loop. Another prerequisite is good preconditioning In mathematics, preconditioning is the application of a transformation, called the preconditioner, that conditions a given problem in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |