|
Lorenz Equation
The Lorenz system is a system of ordinary differential equations first studied by mathematician and meteorologist Edward Lorenz. It is notable for having chaotic solutions for certain parameter values and initial conditions. In particular, the Lorenz attractor is a set of chaotic solutions of the Lorenz system. The term "butterfly effect" in popular media may stem from the real-world implications of the Lorenz attractor, namely that tiny changes in initial conditions evolve to completely different trajectories. This underscores that chaotic systems can be completely deterministic and yet still be inherently impractical or even impossible to predict over longer periods of time. For example, even the small flap of a butterfly's wings could set the earth's atmosphere on a vastly different trajectory, in which for example a hurricane occurs where it otherwise would have not (see Saddle points). The shape of the Lorenz attractor itself, when plotted in phase space, may also be seen to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
A Trajectory Through Phase Space In A Lorenz Attractor
A, or a, is the first letter and the first vowel letter of the Latin alphabet, used in the modern English alphabet, and others worldwide. Its name in English is '' a'' (pronounced ), plural ''aes''. It is similar in shape to the Ancient Greek letter alpha, from which it derives. The uppercase version consists of the two slanting sides of a triangle, crossed in the middle by a horizontal bar. The lowercase version is often written in one of two forms: the double-storey and single-storey . The latter is commonly used in handwriting and fonts based on it, especially fonts intended to be read by children, and is also found in italic type. In English, '' a'' is the indefinite article, with the alternative form ''an''. Name In English, the name of the letter is the ''long A'' sound, pronounced . Its name in most other languages matches the letter's pronunciation in open syllables. History The earliest known ancestor of A is ''aleph''—the first letter of the Phoenician ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prandtl Number
The Prandtl number (Pr) or Prandtl group is a dimensionless number, named after the German physicist Ludwig Prandtl, defined as the ratio of momentum diffusivity to thermal diffusivity. The Prandtl number is given as:where: * \nu : momentum diffusivity ( kinematic viscosity), \nu = \mu/\rho, ( SI units: m2/s) * \alpha : thermal diffusivity, \alpha = k/(\rho c_p), (SI units: m2/s) * \mu : dynamic viscosity, (SI units: Pa s = N s/m2) * k : thermal conductivity, (SI units: W/(m·K)) * c_p : specific heat, (SI units: J/(kg·K)) * \rho : density, (SI units: kg/m3). Note that whereas the Reynolds number and Grashof number are subscripted with a scale variable, the Prandtl number contains no such length scale and is dependent only on the fluid and the fluid state. The Prandtl number is often found in property tables alongside other properties such as viscosity and thermal conductivity. The mass transfer analog of the Prandtl number is the Schmidt number and the ratio of the Pran ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Equilibrium Point (mathematics)
In mathematics, specifically in differential equations, an equilibrium point is a constant solution to a differential equation. Formal definition The point \tilde\in \mathbb^n is an equilibrium point for the differential equation :\frac = \mathbf(t,\mathbf) if \mathbf(t,\tilde)=\mathbf for all t. Similarly, the point \tilde\in \mathbb^n is an equilibrium point (or fixed point) for the difference equation :\mathbf_ = \mathbf(k,\mathbf_k) if \mathbf(k,\tilde)= \tilde for k=0,1,2,\ldots. Equilibria can be classified by looking at the signs of the eigenvalues of the linearization of the equations about the equilibria. That is to say, by evaluating the Jacobian matrix at each of the equilibrium points of the system, and then finding the resulting eigenvalues, the equilibria can be categorized. Then the behavior of the system in the neighborhood of each equilibrium point can be qualitatively determined, (or even quantitatively determined, in some instances), by finding ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Deterministic System (mathematics)
In mathematics, computer science and physics, a deterministic system is a system in which no randomness is involved in the development of future states of the system. A deterministic model will thus always produce the same output from a given starting condition or initial state. In physics Physical laws that are described by differential equations represent deterministic systems, even though the state of the system at a given point in time may be difficult to describe explicitly. In quantum mechanics, the Schrödinger equation, which describes the continuous time evolution of a system's wave function, is deterministic. However, the relationship between a system's wave function and the observable properties of the system appears to be non-deterministic. In mathematics The systems studied in chaos theory are deterministic. If the initial state were known exactly, then the future state of such a system could theoretically be predicted. However, in practice, knowledge about the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nonlinearity
In mathematics and science, a nonlinear system (or a non-linear system) is a system in which the change of the output is not proportional to the change of the input. Nonlinear problems are of interest to engineers, biologists, physicists, mathematicians, and many other scientists since most systems are inherently nonlinear in nature. Nonlinear dynamical systems, describing changes in variables over time, may appear chaotic, unpredictable, or counterintuitive, contrasting with much simpler linear systems. Typically, the behavior of a nonlinear system is described in mathematics by a nonlinear system of equations, which is a set of simultaneous equations in which the unknowns (or the unknown functions in the case of differential equations) appear as variables of a polynomial of degree higher than one or in the argument of a function which is not a polynomial of degree one. In other words, in a nonlinear system of equations, the equation(s) to be solved cannot be written as a li ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Malkus Waterwheel
The Malkus waterwheel, also referred to as the Lorenz waterwheel or chaotic waterwheel, is a mechanical model that exhibits Chaos theory, chaotic dynamics. Its motion is governed by the Lorenz system, Lorenz equations. While classical waterwheels rotate in one direction at a constant speed, the Malkus waterwheel exhibits chaotic motion where its rotation will speed up, slow down, stop, change directions, and oscillate back and forth between combinations of such behaviours in an unpredictable manner. This variant waterwheel was developed by Willem Malkus in the 1960s. As a pedagogic tool, the Malkus waterwheel became a paradigmatic realization of a chaotic system, and is widely used in the teaching of chaos theory. In addition to its pedagogic use, the Malkus waterwheel has been actively studied by researchers in dynamical systems and chaos. In the Malkus waterwheel, a constant flow of water pours in at the top bucket of a simple circular symmetrical waterwheel and the base of e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Phys
Physics is the scientific study of matter, its Elementary particle, fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge which relates to the order of nature, or, in other words, to the regular succession of events." It is one of the most fundamental scientific disciplines. "Physics is one of the most fundamental of the sciences. Scientists of all disciplines use the ideas of physics, including chemists who study the structure of molecules, paleontologists who try to reconstruct how dinosaurs walked, and climatologists who study how human activities affect the atmosphere and oceans. Physics is also the foundation of all engineering and technology. No engineer could design a flat-screen TV, an interplanetary spacecraft, or even a better mousetrap without first understanding the basic laws of physics. (...) You will come to see physics as a towering achievement of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Forward Osmosis
Forward osmosis (FO) is an osmotic process that, like reverse osmosis (RO), uses a semi-permeable membrane to effect separation of water from dissolved solutes. The driving force for this separation is an osmotic pressure gradient, such that a "draw" solution of high concentration (relative to that of the feed solution), is used to induce a net flow of water through the membrane into the draw solution, thus effectively separating the feed water from its solutes. In contrast, the reverse osmosis process uses hydraulic pressure as the driving force for separation, which serves to counteract the osmotic pressure gradient that would otherwise favor water flux from the permeate to the feed. Hence significantly more energy is required for reverse osmosis compared to forward osmosis. The simplest equation describing the relationship between osmotic and hydraulic pressures and water (solvent) flux is: where J_w is water flux, A is the hydraulic permeability of the membrane, Δπ is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chemical Reaction
A chemical reaction is a process that leads to the chemistry, chemical transformation of one set of chemical substances to another. When chemical reactions occur, the atoms are rearranged and the reaction is accompanied by an Gibbs free energy, energy change as new products are generated. Classically, chemical reactions encompass changes that only involve the positions of electrons in the forming and breaking of chemical bonds between atoms, with no change to the Atomic nucleus, nuclei (no change to the elements present), and can often be described by a chemical equation. Nuclear chemistry is a sub-discipline of chemistry that involves the chemical reactions of unstable and radioactive Chemical element, elements where both electronic and nuclear changes can occur. The substance (or substances) initially involved in a chemical reaction are called reagent, reactants or reagents. Chemical reactions are usually characterized by a chemical change, and they yield one or more Product (c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Electric Circuit
An electrical network is an interconnection of electrical components (e.g., battery (electricity), batteries, resistors, inductors, capacitors, switches, transistors) or a model of such an interconnection, consisting of electrical elements (e.g., voltage sources, current sources, Electrical resistance and conductance, resistances, inductances, capacitances). An electrical circuit is a network consisting of a closed loop, giving a return path for the current. Thus all circuits are networks, but not all networks are circuits (although networks without a closed loop are often referred to as "open circuits"). A resistive network is a network containing only resistors and ideal current and voltage sources. Network analysis (electrical circuits), Analysis of resistive networks is less complicated than analysis of networks containing capacitors and inductors. If the sources are constant (Direct current, DC) sources, the result is a DC network. The effective resistance and current dist ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
DC Motor
A DC motor is an electrical motor that uses direct current (DC) to produce mechanical force. The most common types rely on magnetic forces produced by currents in the coils. Nearly all types of DC motors have some internal mechanism, either electromechanical or electronic, to periodically change the direction of current in part of the motor. DC motors were the first form of motors to be widely used, as they could be powered from existing direct-current lighting power distribution systems. A DC motor's speed can be controlled over a wide range, using either a variable supply voltage or by changing the strength of current in its field windings. Small DC motors are used in tools, toys, and appliances. The universal motor, a lightweight brushed motor used for portable power tools and appliances can operate on direct current and alternating current. Larger DC motors are currently used in propulsion of electric vehicles, elevator and hoists, and in drives for steel rolling mills. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
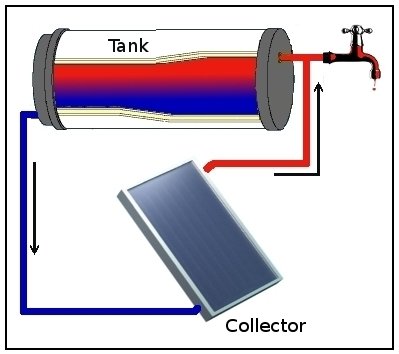
Thermosyphon
A thermosiphon (or thermosyphon) is a device that employs a method of passive heat transfer, heat exchange based on natural convection, which circulates a fluid without the necessity of a mechanical pump. Thermosiphoning is used for circulation of liquids and volatile gases in heating and cooling applications such as heat pumps, water heaters, boilers and furnaces. Thermosiphoning also occurs across air temperature gradients such as those occurring in a wood-fire chimney or solar chimney. This circulation can either be open-loop, as when the substance in a holding tank is passed in one direction via a heated transfer tube mounted at the bottom of the tank to a distribution point — even one mounted above the originating tank — or it can be a vertical closed-loop circuit with return to the original container. Its purpose is to simplify the transfer of liquid or gas while avoiding the cost and complexity of a conventional pump. Simple thermosiphon Natural convection of the liq ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |