Lexell's Theorem
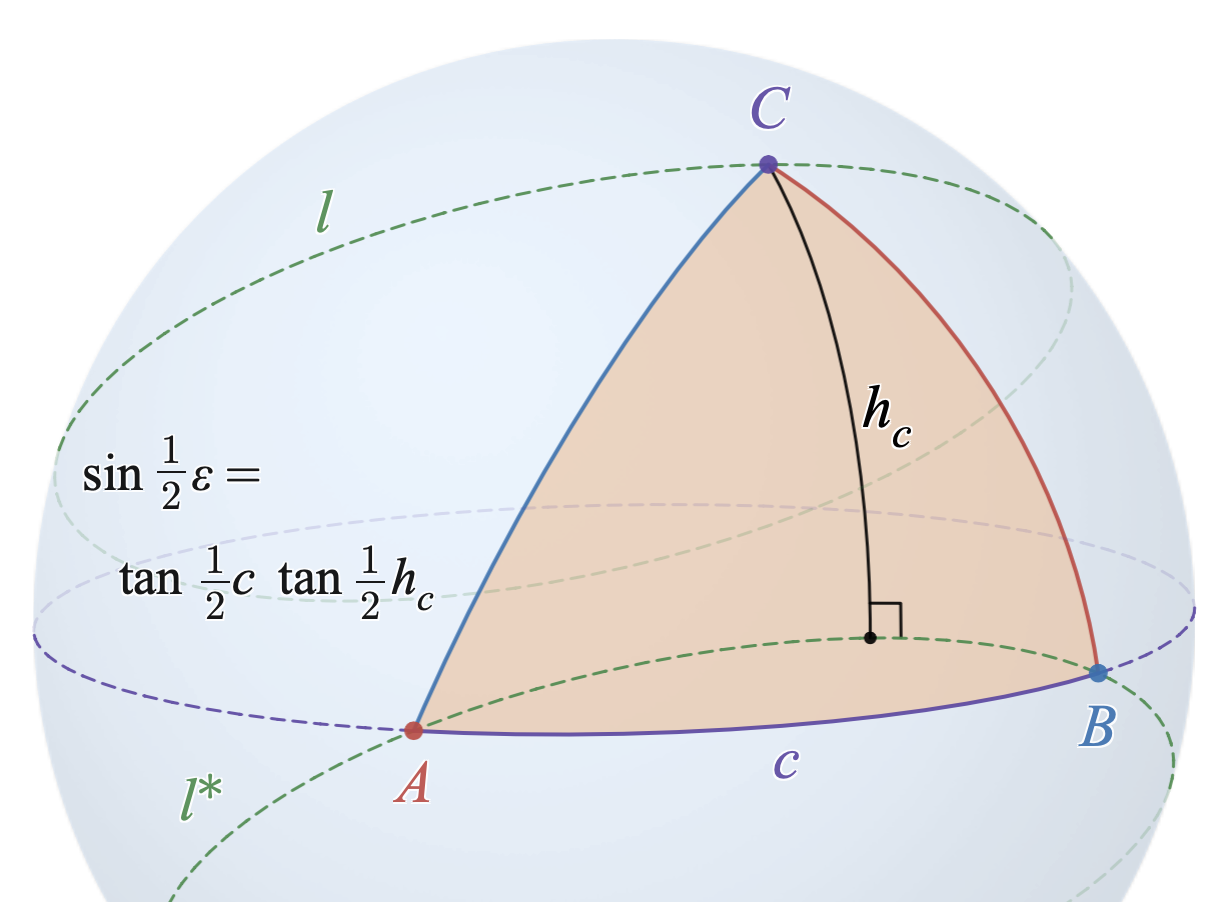
In spherical geometry, Lexell's theorem holds that every spherical triangle with the same surface area on a fixed base (geometry), base has its apex (geometry), apex on a small circle, called ''Lexell's circle'' or ''Lexell's locus (geometry), locus'', passing through each of the two points antipodal point, antipodal to the two base vertex (geometry), vertices. A ''spherical triangle'' is a shape on a sphere consisting of three vertices (corner point (geometry), points) connected by three sides, each of which is part of a ''great circle'' (the analog on the sphere of a straight line in the Euclidean plane, plane, for example the equator and meridian (geography), meridians of a globe). Any of the sides of a spherical triangle can be considered the ''base'', and the opposite vertex is the corresponding ''apex''. Two points on a sphere are ''antipodal'' if they are diametrically opposite, as far apart as possible. The theorem is named for Anders Johan Lexell, who presented a paper ...
[...More Info...]       [...Related Items...]     OR:     [Wikipedia]   [Google]   [Baidu]