|
Krogh Model
Krogh model is a scientific model of mass transfer explaining the concentration of molecular oxygen through a cylindrical capillary tube as a function of a changing position over the capillary tube's length. It was first conceptualized by August Krogh in 1919 with the help of Agner Krarup Erlang to describe oxygen supply in living tissues from human blood vessels. Its applicability has been extended to various academic fields, and has been successful explaining drug diffusion, water transport, and ice formation in tissues. Mathematical modeling Krogh model is derived by applying Fick's laws of diffusion Fick's laws of diffusion describe diffusion and were derived by Adolf Fick in 1855. They can be used to solve for the diffusion coefficient, . Fick's first law can be used to derive his second law which in turn is identical to the diffusion ... and the law of conservation of mass over a radial interval Rc \le r \le Rt Limitations Although Krogh model is a good appro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Scientific Modelling
Scientific modelling is a scientific activity, the aim of which is to make a particular part or feature of the world easier to understand, define, quantify, visualize, or simulate by referencing it to existing and usually commonly accepted knowledge. It requires selecting and identifying relevant aspects of a situation in the real world and then developing a model to replicate a system with those features. Different types of models may be used for different purposes, such as conceptual models to better understand, operational models to operationalize, mathematical models to quantify, computational models to simulate, and graphical models to visualize the subject. Modelling is an essential and inseparable part of many scientific disciplines, each of which has its own ideas about specific types of modelling. The following was said by John von Neumann. There is also an increasing attention to scientific modelling in fields such as science education, philosophy of scienc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conservation Of Mass
In physics and chemistry, the law of conservation of mass or principle of mass conservation states that for any system closed to all transfers of matter and energy, the mass of the system must remain constant over time, as the system's mass cannot change, so quantity can neither be added nor be removed. Therefore, the quantity of mass is conserved over time. The law implies that mass can neither be created nor destroyed, although it may be rearranged in space, or the entities associated with it may be changed in form. For example, in chemical reactions, the mass of the chemical components before the reaction is equal to the mass of the components after the reaction. Thus, during any chemical reaction and low-energy thermodynamic processes in an isolated system, the total mass of the reactants, or starting materials, must be equal to the mass of the products. The concept of mass conservation is widely used in many fields such as chemistry, mechanics, and fluid dynamics. Hist ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diffusion
Diffusion is the net movement of anything (for example, atoms, ions, molecules, energy) generally from a region of higher concentration to a region of lower concentration. Diffusion is driven by a gradient in Gibbs free energy or chemical potential. It is possible to diffuse "uphill" from a region of lower concentration to a region of higher concentration, like in spinodal decomposition. The concept of diffusion is widely used in many fields, including physics (particle diffusion), chemistry, biology, sociology, economics, and finance (diffusion of people, ideas, and price values). The central idea of diffusion, however, is common to all of these: a substance or collection undergoing diffusion spreads out from a point or location at which there is a higher concentration of that substance or collection. A gradient is the change in the value of a quantity, for example, concentration, pressure, or temperature with the change in another variable, usually distance. A change in c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Transport Phenomena
In engineering, physics, and chemistry, the study of transport phenomena concerns the exchange of mass, energy, charge, momentum and angular momentum between observed and studied systems. While it draws from fields as diverse as continuum mechanics and thermodynamics, it places a heavy emphasis on the commonalities between the topics covered. Mass, momentum, and heat transport all share a very similar mathematical framework, and the parallels between them are exploited in the study of transport phenomena to draw deep mathematical connections that often provide very useful tools in the analysis of one field that are directly derived from the others. The fundamental analysis in all three subfields of mass, heat, and momentum transfer are often grounded in the simple principle that the total sum of the quantities being studied must be conserved by the system and its environment. Thus, the different phenomena that lead to transport are each considered individually with the knowled ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
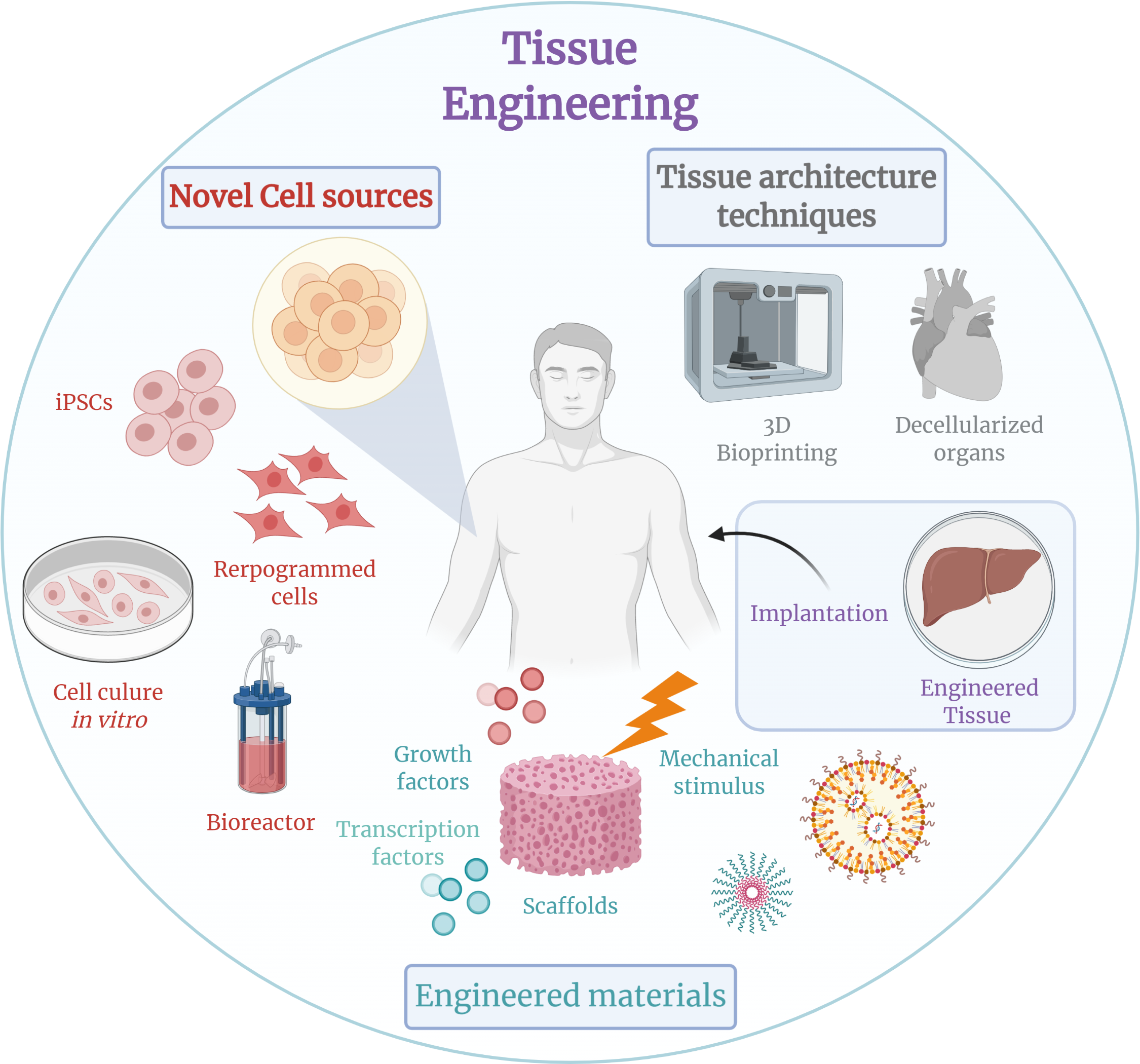
Tissue Engineering
Tissue engineering is a biomedical engineering discipline that uses a combination of cells, engineering, materials methods, and suitable biochemical and physicochemical factors to restore, maintain, improve, or replace different types of biological tissues. Tissue engineering often involves the use of cells placed on tissue scaffolds in the formation of new viable tissue for a medical purpose but is not limited to applications involving cells and tissue scaffolds. While it was once categorized as a sub-field of biomaterials, having grown in scope and importance it can be considered as a field of its own. While most definitions of tissue engineering cover a broad range of applications, in practice the term is closely associated with applications that repair or replace portions of or whole tissues (i.e. bone, cartilage, blood vessels, bladder, skin, muscle etc.). Often, the tissues involved require certain mechanical and structural properties for proper functioning. The term has al ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chemical Engineering
Chemical engineering is an engineering field which deals with the study of operation and design of chemical plants as well as methods of improving production. Chemical engineers develop economical commercial processes to convert raw materials into useful products. Chemical engineering uses principles of chemistry, physics, mathematics, biology, and economics to efficiently use, produce, design, transport and transform energy and materials. The work of chemical engineers can range from the utilization of nanotechnology and nanomaterials in the laboratory to large-scale industrial processes that convert chemicals, raw materials, living cells, microorganisms, and energy into useful forms and products. Chemical engineers are involved in many aspects of plant design and operation, including safety and hazard assessments, process design and analysis, modeling, control engineering, chemical reaction engineering, nuclear engineering, biological engineering, construction specificati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bioengineering
Biological engineering or bioengineering is the application of principles of biology and the tools of engineering to create usable, tangible, economically-viable products. Biological engineering employs knowledge and expertise from a number of pure and applied sciences, such as mass and heat transfer, kinetics, biocatalysts, biomechanics, bioinformatics, separation and purification processes, bioreactor design, surface science, fluid mechanics, thermodynamics, and polymer science. It is used in the design of medical devices, diagnostic equipment, biocompatible materials, renewable energy, ecological engineering, agricultural engineering, process engineering and catalysis, and other areas that improve the living standards of societies. Examples of bioengineering research include bacteria engineered to produce chemicals, new medical imaging technology, portable and rapid disease diagnostic devices, prosthetics, biopharmaceuticals, and tissue-engineered organs. Bioengineering ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Interval (mathematics)
In mathematics, a (real) interval is a set of real numbers that contains all real numbers lying between any two numbers of the set. For example, the set of numbers satisfying is an interval which contains , , and all numbers in between. Other examples of intervals are the set of numbers such that , the set of all real numbers \R, the set of nonnegative real numbers, the set of positive real numbers, the empty set, and any singleton (set of one element). Real intervals play an important role in the theory of integration, because they are the simplest sets whose "length" (or "measure" or "size") is easy to define. The concept of measure can then be extended to more complicated sets of real numbers, leading to the Borel measure and eventually to the Lebesgue measure. Intervals are central to interval arithmetic, a general numerical computing technique that automatically provides guaranteed enclosures for arbitrary formulas, even in the presence of uncertainties, mathematic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fick's Laws Of Diffusion
Fick's laws of diffusion describe diffusion and were derived by Adolf Fick in 1855. They can be used to solve for the diffusion coefficient, . Fick's first law can be used to derive his second law which in turn is identical to the diffusion equation. A diffusion process that obeys Fick's laws is called normal or Fickian diffusion; otherwise, it is called anomalous diffusion or non-Fickian diffusion. History In 1855, physiologist Adolf Fick first reported* * his now well-known laws governing the transport of mass through diffusive means. Fick's work was inspired by the earlier experiments of Thomas Graham, which fell short of proposing the fundamental laws for which Fick would become famous. Fick's law is analogous to the relationships discovered at the same epoch by other eminent scientists: Darcy's law (hydraulic flow), Ohm's law (charge transport), and Fourier's Law (heat transport). Fick's experiments (modeled on Graham's) dealt with measuring the concentration ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mass Transfer
Mass transfer is the net movement of mass from one location (usually meaning stream, phase, fraction or component) to another. Mass transfer occurs in many processes, such as absorption, evaporation, drying, precipitation, membrane filtration, and distillation. Mass transfer is used by different scientific disciplines for different processes and mechanisms. The phrase is commonly used in engineering for physical processes that involve diffusive and convective transport of chemical species within physical systems. Some common examples of mass transfer processes are the evaporation of water from a pond to the atmosphere, the purification of blood in the kidneys and liver, and the distillation of alcohol. In industrial processes, mass transfer operations include separation of chemical components in distillation columns, absorbers such as scrubbers or stripping, adsorbers such as activated carbon beds, and liquid-liquid extraction. Mass transfer is often coupled to additi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Blood Vessel
Blood vessels are the structures of the circulatory system that transport blood throughout the human body. These vessels transport blood cells, nutrients, and oxygen to the tissues of the body. They also take waste and carbon dioxide away from the tissues. Blood vessels are needed to sustain life, because all of the body's tissues rely on their functionality. There are five types of blood vessels: the arteries, which carry the blood away from the heart; the arterioles; the capillaries, where the exchange of water and chemicals between the blood and the tissues occurs; the venules; and the veins, which carry blood from the capillaries back towards the heart. The word ''vascular'', meaning relating to the blood vessels, is derived from the Latin ''vas'', meaning vessel. Some structures – such as cartilage, the epithelium, and the lens and cornea of the eye – do not contain blood vessels and are labeled ''avascular''. Etymology * artery: late Middle English; from ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Agner Krarup Erlang
Agner Krarup Erlang (1 January 1878 – 3 February 1929) was a Danish mathematician, statistician and engineer, who invented the fields of traffic engineering and queueing theory. By the time of his relatively early death at the age of 51, Erlang had created the field of telephone networks analysis. His early work in scrutinizing the use of local, exchange and trunk telephone line usage in a small community to understand the theoretical requirements of an efficient network led to the creation of the Erlang formula, which became a foundational element of modern telecommunication network studies. Life Erlang was born at Lønborg, near Tarm, in Jutland. He was the son of a schoolmaster, and a descendant of Thomas Fincke on his mother's side. At age 14, he passed the Preliminary Examination of the University of Copenhagen with distinction, after receiving dispensation to take it because he was younger than the usual minimum age. For the next two years he taught alongside ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |