|
Kramers' Theorem
In quantum mechanics, Kramers' theorem or Kramers' degeneracy theorem states that for every energy eigenstate of a time-reversal symmetric system with half-integer total spin, there is another eigenstate with the same energy related by time-reversal. In other words, the degeneracy of every energy level is an even number if it has half-integer spin. The theorem is named after Dutch physicist H. A. Kramers. In theoretical physics, the time reversal symmetry is the symmetry of physical laws under a time reversal transformation: : T: t \mapsto -t. If the Hamiltonian operator commutes with the time-reversal operator, that is : ,T0, then, for every energy eigenstate , n\rangle, the time reversed state T, n\rangle is also an eigenstate with the same energy. These two states are sometimes called a Kramers pair. In general, this time-reversed state may be identical to the original one, but that is not possible in a half-integer spin system: since time reversal reverses all angular moment ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Mechanics
Quantum mechanics is the fundamental physical Scientific theory, theory that describes the behavior of matter and of light; its unusual characteristics typically occur at and below the scale of atoms. Reprinted, Addison-Wesley, 1989, It is the foundation of all quantum physics, which includes quantum chemistry, quantum field theory, quantum technology, and quantum information science. Quantum mechanics can describe many systems that classical physics cannot. Classical physics can describe many aspects of nature at an ordinary (macroscopic and Microscopic scale, (optical) microscopic) scale, but is not sufficient for describing them at very small submicroscopic (atomic and subatomic) scales. Classical mechanics can be derived from quantum mechanics as an approximation that is valid at ordinary scales. Quantum systems have Bound state, bound states that are Quantization (physics), quantized to Discrete mathematics, discrete values of energy, momentum, angular momentum, and ot ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Energy Level
A quantum mechanics, quantum mechanical system or particle that is bound state, bound—that is, confined spatially—can only take on certain discrete values of energy, called energy levels. This contrasts with classical mechanics, classical particles, which can have any amount of energy. The term is commonly used for the energy levels of the electrons in atoms, ions, or molecules, which are bound by the electric field of the atomic nucleus, nucleus, but can also refer to energy levels of nuclei or molecular vibration, vibrational or rotational energy levels in molecules. The energy spectrum of a system with such discrete energy levels is said to be Quantization (physics), quantized. In chemistry and atomic physics, an electron shell, or principal energy level, may be thought of as the orbit of one or more electrons around an atom's atomic nucleus, nucleus. The closest shell to the nucleus is called the "1 shell" (also called "K shell"), followed by the "2 shell" (or "L shell"), ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Degenerate Energy Levels
In quantum mechanics, an energy level is degenerate if it corresponds to two or more different measurable states of a quantum system. Conversely, two or more different states of a quantum mechanical system are said to be degenerate if they give the same value of energy upon measurement. The number of different states corresponding to a particular energy level is known as the ''degree of degeneracy'' (or simply the ''degeneracy'') of the level. It is represented mathematically by the Hamiltonian for the system having more than one linearly independent eigenstate with the same energy eigenvalue. When this is the case, energy alone is not enough to characterize what state the system is in, and other quantum numbers are needed to characterize the exact state when distinction is desired. In classical mechanics, this can be understood in terms of different possible trajectories corresponding to the same energy. Degeneracy plays a fundamental role in quantum statistical mechanics. For ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
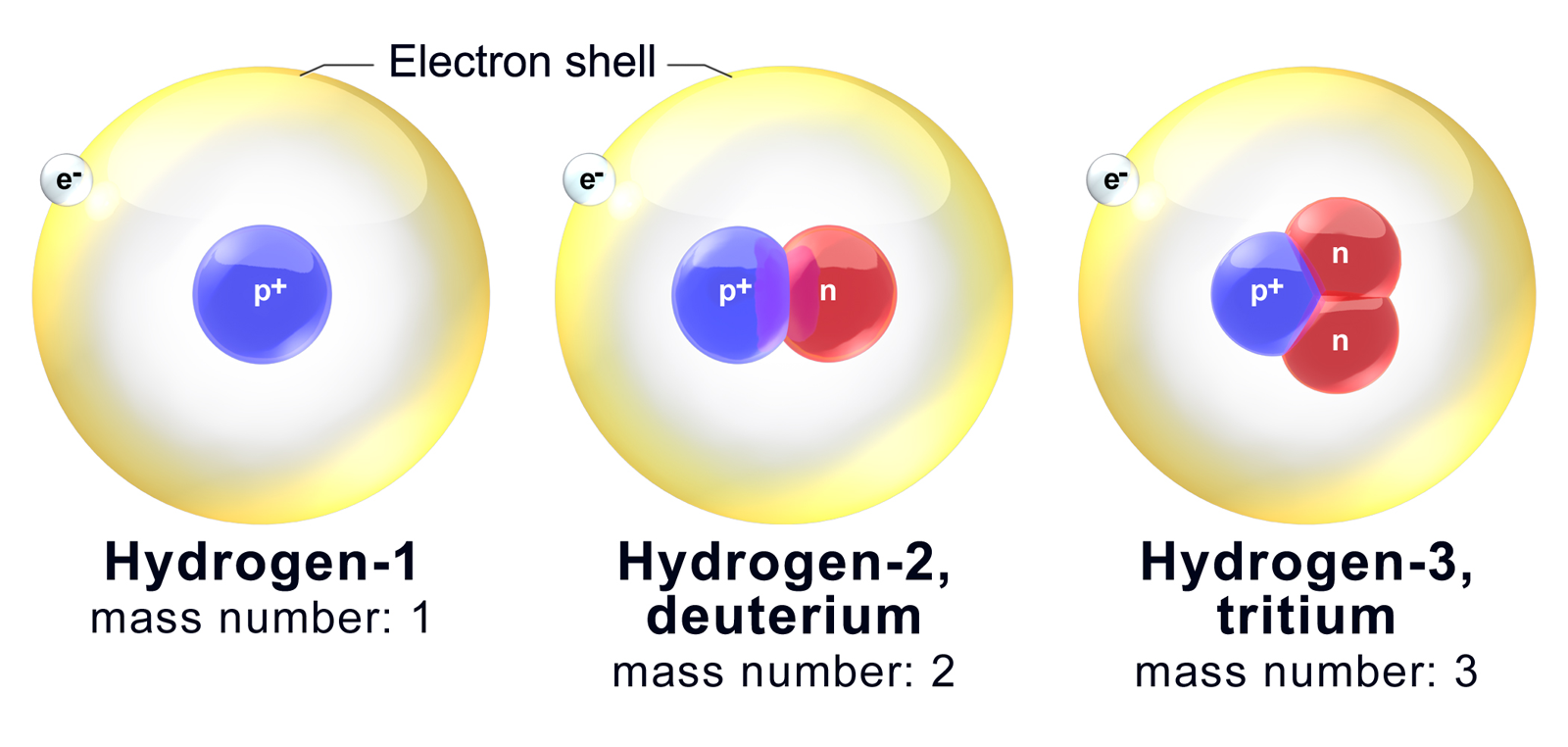
Deuterium
Deuterium (hydrogen-2, symbol H or D, also known as heavy hydrogen) is one of two stable isotopes of hydrogen; the other is protium, or hydrogen-1, H. The deuterium nucleus (deuteron) contains one proton and one neutron, whereas the far more common H has no neutrons. The name ''deuterium'' comes from Greek '' deuteros'', meaning "second". American chemist Harold Urey discovered deuterium in 1931. Urey and others produced samples of heavy water in which the H had been highly concentrated. The discovery of deuterium won Urey a Nobel Prize in 1934. Nearly all deuterium found in nature was synthesized in the Big Bang 13.8 billion years ago, forming the primordial ratio of H to H (~26 deuterium nuclei per 10 hydrogen nuclei). Deuterium is subsequently produced by the slow stellar proton–proton chain, but rapidly destroyed by exothermic fusion reactions. The deuterium–deuterium reaction has the second-lowest energy threshold, and is the most astrophysically acce ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hydrogen
Hydrogen is a chemical element; it has chemical symbol, symbol H and atomic number 1. It is the lightest and abundance of the chemical elements, most abundant chemical element in the universe, constituting about 75% of all baryon, normal matter. Under standard conditions, hydrogen is a gas of diatomic molecules with the chemical formula, formula , called dihydrogen, or sometimes hydrogen gas, molecular hydrogen, or simply hydrogen. Dihydrogen is colorless, odorless, non-toxic, and highly combustible. Stars, including the Sun, mainly consist of hydrogen in a plasma state, while on Earth, hydrogen is found as the gas (dihydrogen) and in molecular forms, such as in water and organic compounds. The most common isotope of hydrogen (H) consists of one proton, one electron, and no neutrons. Hydrogen gas was first produced artificially in the 17th century by the reaction of acids with metals. Henry Cavendish, in 1766–1781, identified hydrogen gas as a distinct substance and discovere ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Antiunitary
In mathematics, an antiunitary transformation is a bijective antilinear map :U: H_1 \to H_2\, between two complex Hilbert spaces such that :\langle Ux, Uy \rangle = \overline for all x and y in H_1, where the horizontal bar represents the complex conjugate. If additionally one has H_1 = H_2 then U is called an antiunitary operator. Antiunitary operators are important in quantum mechanics because they are used to represent certain symmetries, such as time reversal. Their fundamental importance in quantum physics is further demonstrated by Wigner's theorem. Invariance transformations In quantum mechanics, the invariance transformations of complex Hilbert space H leave the absolute value of scalar product invariant: : , \langle Tx, Ty \rangle, = , \langle x, y \rangle, for all x and y in H. Due to Wigner's theorem these transformations can either be unitary or antiunitary. Geometric Interpretation Congruences of the plane form two distinct classes. The first conserv ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Time Reversal Invariance
T-symmetry or time reversal symmetry is the theoretical symmetry of physical laws under the transformation of time reversal, : T: t \mapsto -t. Since the second law of thermodynamics states that entropy increases as time flows toward the future, in general, the macroscopic universe does not show symmetry under time reversal. In other words, time is said to be non-symmetric, or asymmetric, except for special equilibrium states when the second law of thermodynamics predicts the time symmetry to hold. However, quantum noninvasive measurements are predicted to violate time symmetry even in equilibrium, contrary to their classical counterparts, although this has not yet been experimentally confirmed. Time ''asymmetries'' (see Arrow of time) generally are caused by one of three categories: # intrinsic to the dynamic physical law (e.g., for the weak force) # due to the initial conditions of the universe (e.g., for the second law of thermodynamics) # due to measurements (e.g., for th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eugene Wigner
Eugene Paul Wigner (, ; November 17, 1902 – January 1, 1995) was a Hungarian-American theoretical physicist who also contributed to mathematical physics. He received the Nobel Prize in Physics in 1963 "for his contributions to the theory of the atomic nucleus and the elementary particles, particularly through the discovery and application of fundamental symmetry principles". A graduate of the Technical Hochschule Berlin (now Technische Universität Berlin), Wigner worked as an assistant to Karl Weissenberg and Richard Becker (physicist), Richard Becker at the Max Planck Institute for Physics, Kaiser Wilhelm Institute in Berlin, and David Hilbert at the University of Göttingen. Wigner and Hermann Weyl were responsible for introducing group theory into physics, particularly the theory of symmetry in physics. Along the way he performed ground-breaking work in pure mathematics, in which he authored a number of mathematical theorems. In particular, Wigner's theorem is a cornerstone ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Breit Equation
The Breit equation, or Dirac–Coulomb–Breit equation, is a relativistic wave equation derived by Gregory Breit in 1929 based on the Dirac equation, which formally describes two or more massive spin-1/2 particles (electrons, for example) interacting electromagnetically to the first order in perturbation theory. It accounts for magnetic interactions and retardation effects to the order of 1/''c''2. When other quantum electrodynamic effects are negligible, this equation has been shown to give results in good agreement with experiment. It was originally derived from the Darwin Lagrangian but later vindicated by the Wheeler–Feynman absorber theory and eventually quantum electrodynamics. Introduction The Breit equation is not only an approximation in terms of quantum mechanics, but also in terms of relativity theory as it is not completely invariant with respect to the Lorentz transformation. Just as does the Dirac equation, it treats nuclei as point sources of an external field ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Magnetic Field
A magnetic field (sometimes called B-field) is a physical field that describes the magnetic influence on moving electric charges, electric currents, and magnetic materials. A moving charge in a magnetic field experiences a force perpendicular to its own velocity and to the magnetic field. A permanent magnet's magnetic field pulls on ferromagnetic materials such as iron, and attracts or repels other magnets. In addition, a nonuniform magnetic field exerts minuscule forces on "nonmagnetic" materials by three other magnetic effects: paramagnetism, diamagnetism, and antiferromagnetism, although these forces are usually so small they can only be detected by laboratory equipment. Magnetic fields surround magnetized materials, electric currents, and electric fields varying in time. Since both strength and direction of a magnetic field may vary with location, it is described mathematically by a function (mathematics), function assigning a Euclidean vector, vector to each point of space, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Electric Field
An electric field (sometimes called E-field) is a field (physics), physical field that surrounds electrically charged particles such as electrons. In classical electromagnetism, the electric field of a single charge (or group of charges) describes their capacity to exert attractive or repulsive forces on another charged object. Charged particles exert attractive forces on each other when the sign of their charges are opposite, one being positive while the other is negative, and repel each other when the signs of the charges are the same. Because these forces are exerted mutually, two charges must be present for the forces to take place. These forces are described by Coulomb's law, which says that the greater the magnitude of the charges, the greater the force, and the greater the distance between them, the weaker the force. Informally, the greater the charge of an object, the stronger its electric field. Similarly, an electric field is stronger nearer charged objects and weaker f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Degenerate Energy Level
In quantum mechanics, an energy level is degenerate if it corresponds to two or more different measurable states of a quantum system. Conversely, two or more different states of a quantum mechanical system are said to be degenerate if they give the same value of energy upon measurement. The number of different states corresponding to a particular energy level is known as the ''degree of degeneracy'' (or simply the ''degeneracy'') of the level. It is represented mathematically by the Hamiltonian (quantum mechanics), Hamiltonian for the system having more than one linear independence, linearly independent eigenstate with the same energy eigenvalue. When this is the case, energy alone is not enough to characterize what state the system is in, and other quantum numbers are needed to characterize the exact state when distinction is desired. In classical mechanics, this can be understood in terms of different possible trajectories corresponding to the same energy. Degeneracy plays a fu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |