|
Kernel Embedding Of Distributions
In machine learning, the kernel embedding of distributions (also called the kernel mean or mean map) comprises a class of nonparametric methods in which a probability distribution is represented as an element of a reproducing kernel Hilbert space (RKHS).A. Smola, A. Gretton, L. Song, B. Schölkopf. (2007)A Hilbert Space Embedding for Distributions. ''Algorithmic Learning Theory: 18th International Conference''. Springer: 13–31. A generalization of the individual data-point feature mapping done in classical kernel methods, the embedding of distributions into infinite-dimensional feature spaces can preserve all of the statistical features of arbitrary distributions, while allowing one to compare and manipulate distributions using Hilbert space operations such as inner products, distances, projections, linear transformations, and spectral analysis.L. Song, K. Fukumizu, F. Dinuzzo, A. Gretton (2013)Kernel Embeddings of Conditional Distributions: A unified kernel framework for n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Machine Learning
Machine learning (ML) is a field of study in artificial intelligence concerned with the development and study of Computational statistics, statistical algorithms that can learn from data and generalise to unseen data, and thus perform Task (computing), tasks without explicit Machine code, instructions. Within a subdiscipline in machine learning, advances in the field of deep learning have allowed Neural network (machine learning), neural networks, a class of statistical algorithms, to surpass many previous machine learning approaches in performance. ML finds application in many fields, including natural language processing, computer vision, speech recognition, email filtering, agriculture, and medicine. The application of ML to business problems is known as predictive analytics. Statistics and mathematical optimisation (mathematical programming) methods comprise the foundations of machine learning. Data mining is a related field of study, focusing on exploratory data analysi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bernhard Schölkopf
Bernhard Schölkopf (born 20 February 1968) is a German computer scientist known for his work in machine learning, especially on kernel methods and causality. He is a director at the Max Planck Institute for Intelligent Systems in Tübingen, Germany, where he heads the Department of Empirical Inference. He is also an affiliated professor at ETH Zürich, honorary professor at the University of Tübingen and Technische Universität Berlin, and chairman of the European Laboratory for Learning and Intelligent Systems (ELLIS). Research Kernel methods Schölkopf developed SVM methods achieving world record performance on the MNIST pattern recognition benchmark at the time. With the introduction of kernel PCA, Schölkopf and coauthors argued that SVMs are a special case of a much larger class of methods, and all algorithms that can be expressed in terms of dot products can be generalized to a nonlinear setting by means of what is known as reproducing kernels. Another signific ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hilbert Space
In mathematics, a Hilbert space is a real number, real or complex number, complex inner product space that is also a complete metric space with respect to the metric induced by the inner product. It generalizes the notion of Euclidean space. The inner product allows lengths and angles to be defined. Furthermore, Complete metric space, completeness means that there are enough limit (mathematics), limits in the space to allow the techniques of calculus to be used. A Hilbert space is a special case of a Banach space. Hilbert spaces were studied beginning in the first decade of the 20th century by David Hilbert, Erhard Schmidt, and Frigyes Riesz. They are indispensable tools in the theories of partial differential equations, mathematical formulation of quantum mechanics, quantum mechanics, Fourier analysis (which includes applications to signal processing and heat transfer), and ergodic theory (which forms the mathematical underpinning of thermodynamics). John von Neumann coined the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Reproducing Kernel Hilbert Space
In functional analysis, a reproducing kernel Hilbert space (RKHS) is a Hilbert space of functions in which point evaluation is a continuous linear functional. Specifically, a Hilbert space H of functions from a set X (to \mathbb or \mathbb) is an RKHS if the point-evaluation functional L_x:H\to\mathbb, L_x(f)=f(x), is continuous for every x\in X. Equivalently, H is an RKHS if there exists a function K_x \in H such that, for all f \in H,\langle f, K_x \rangle = f(x).The function K_x is then called the ''reproducing kernel'', and it reproduces the value of f at x via the inner product. An immediate consequence of this property is that convergence in norm implies uniform convergence on any subset of X on which \, K_x\, is bounded. However, the converse does not necessarily hold. Often the set X carries a topology, and \, K_x\, depends continuously on x\in X, in which case: convergence in norm implies uniform convergence on compact subsets of X. It is not entirely straightforwar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Positive-definite Kernel
In operator theory, a branch of mathematics, a positive-definite kernel is a generalization of a positive-definite function or a positive-definite matrix. It was first introduced by James Mercer in the early 20th century, in the context of solving integral operator equations. Since then, positive-definite functions and their various analogues and generalizations have arisen in diverse parts of mathematics. They occur naturally in Fourier analysis, probability theory, operator theory, complex function-theory, moment problems, integral equations, boundary-value problems for partial differential equations, machine learning, embedding problem, information theory, and other areas. Definition Let \mathcal X be a nonempty set, sometimes referred to as the index set. A symmetric function K: \mathcal X \times \mathcal X \to \mathbb is called a positive-definite (p.d.) kernel on \mathcal X if holds for all x_1, \dots, x_n\in \mathcal X, n\in \mathbb, c_1, \dots, c_n \in \mathbb. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gramian Matrix
In linear algebra, the Gram matrix (or Gramian matrix, Gramian) of a set of vectors v_1,\dots, v_n in an inner product space is the Hermitian matrix of inner products, whose entries are given by the inner product G_ = \left\langle v_i, v_j \right\rangle., p.441, Theorem 7.2.10 If the vectors v_1,\dots, v_n are the columns of matrix X then the Gram matrix is X^\dagger X in the general case that the vector coordinates are complex numbers, which simplifies to X^\top X for the case that the vector coordinates are real numbers. An important application is to compute linear independence: a set of vectors are linearly independent if and only if the Gram determinant (the determinant of the Gram matrix) is non-zero. It is named after Jørgen Pedersen Gram. Examples For finite-dimensional real vectors in \mathbb^n with the usual Euclidean dot product, the Gram matrix is G = V^\top V, where V is a matrix whose columns are the vectors v_k and V^\top is its transpose whose rows are the vect ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kernel Trick
In machine learning, kernel machines are a class of algorithms for pattern analysis, whose best known member is the support-vector machine (SVM). These methods involve using linear classifiers to solve nonlinear problems. The general task of pattern analysis is to find and study general types of relations (for example clusters, rankings, principal components, correlations, classifications) in datasets. For many algorithms that solve these tasks, the data in raw representation have to be explicitly transformed into feature vector representations via a user-specified ''feature map'': in contrast, kernel methods require only a user-specified ''kernel'', i.e., a similarity function over all pairs of data points computed using inner products. The feature map in kernel machines is infinite dimensional but only requires a finite dimensional matrix from user-input according to the representer theorem. Kernel machines are slow to compute for datasets larger than a couple of thousand ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fourier Transform
In mathematics, the Fourier transform (FT) is an integral transform that takes a function as input then outputs another function that describes the extent to which various frequencies are present in the original function. The output of the transform is a complex-valued function of frequency. The term ''Fourier transform'' refers to both this complex-valued function and the mathematical operation. When a distinction needs to be made, the output of the operation is sometimes called the frequency domain representation of the original function. The Fourier transform is analogous to decomposing the sound of a musical chord into the intensities of its constituent pitches. Functions that are localized in the time domain have Fourier transforms that are spread out across the frequency domain and vice versa, a phenomenon known as the uncertainty principle. The critical case for this principle is the Gaussian function, of substantial importance in probability theory and statist ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Characteristic Function (probability Theory)
In probability theory and statistics, the characteristic function of any real-valued random variable completely defines its probability distribution. If a random variable admits a probability density function, then the characteristic function is the Fourier transform (with sign reversal) of the probability density function. Thus it provides an alternative route to analytical results compared with working directly with probability density functions or cumulative distribution functions. There are particularly simple results for the characteristic functions of distributions defined by the weighted sums of random variables. In addition to univariate distributions, characteristic functions can be defined for vector- or matrix-valued random variables, and can also be extended to more generic cases. The characteristic function always exists when treated as a function of a real-valued argument, unlike the moment-generating function. There are relations between the behavior of the charact ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kernel Density Estimation
In statistics, kernel density estimation (KDE) is the application of kernel smoothing for probability density estimation, i.e., a non-parametric method to estimate the probability density function of a random variable based on '' kernels'' as weights. KDE answers a fundamental data smoothing problem where inferences about the population are made based on a finite data sample. In some fields such as signal processing and econometrics it is also termed the Parzen–Rosenblatt window method, after Emanuel Parzen and Murray Rosenblatt, who are usually credited with independently creating it in its current form. One of the famous applications of kernel density estimation is in estimating the class-conditional marginal densities of data when using a naive Bayes classifier, which can improve its prediction accuracy. Definition Let be independent and identically distributed samples drawn from some univariate distribution with an unknown density at any given point . We are in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mixture Model
In statistics, a mixture model is a probabilistic model for representing the presence of subpopulations within an overall population, without requiring that an observed data set should identify the sub-population to which an individual observation belongs. Formally a mixture model corresponds to the mixture distribution that represents the probability distribution of observations in the overall population. However, while problems associated with "mixture distributions" relate to deriving the properties of the overall population from those of the sub-populations, "mixture models" are used to make statistical inferences about the properties of the sub-populations given only observations on the pooled population, without sub-population identity information. Mixture models are used for clustering, under the name model-based clustering, and also for density estimation. Mixture models should not be confused with models for compositional data, i.e., data whose components are constra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
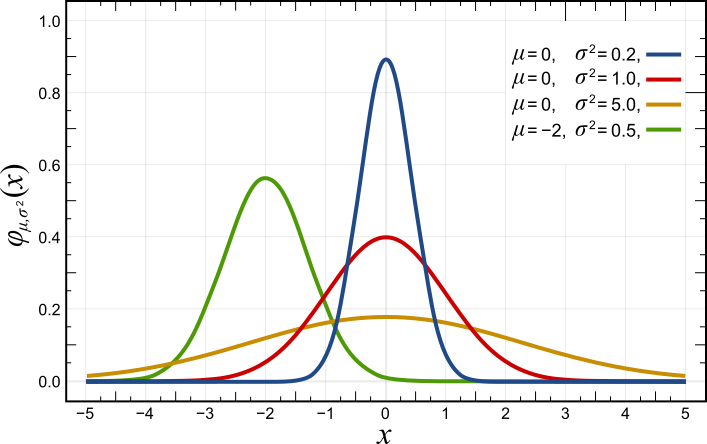
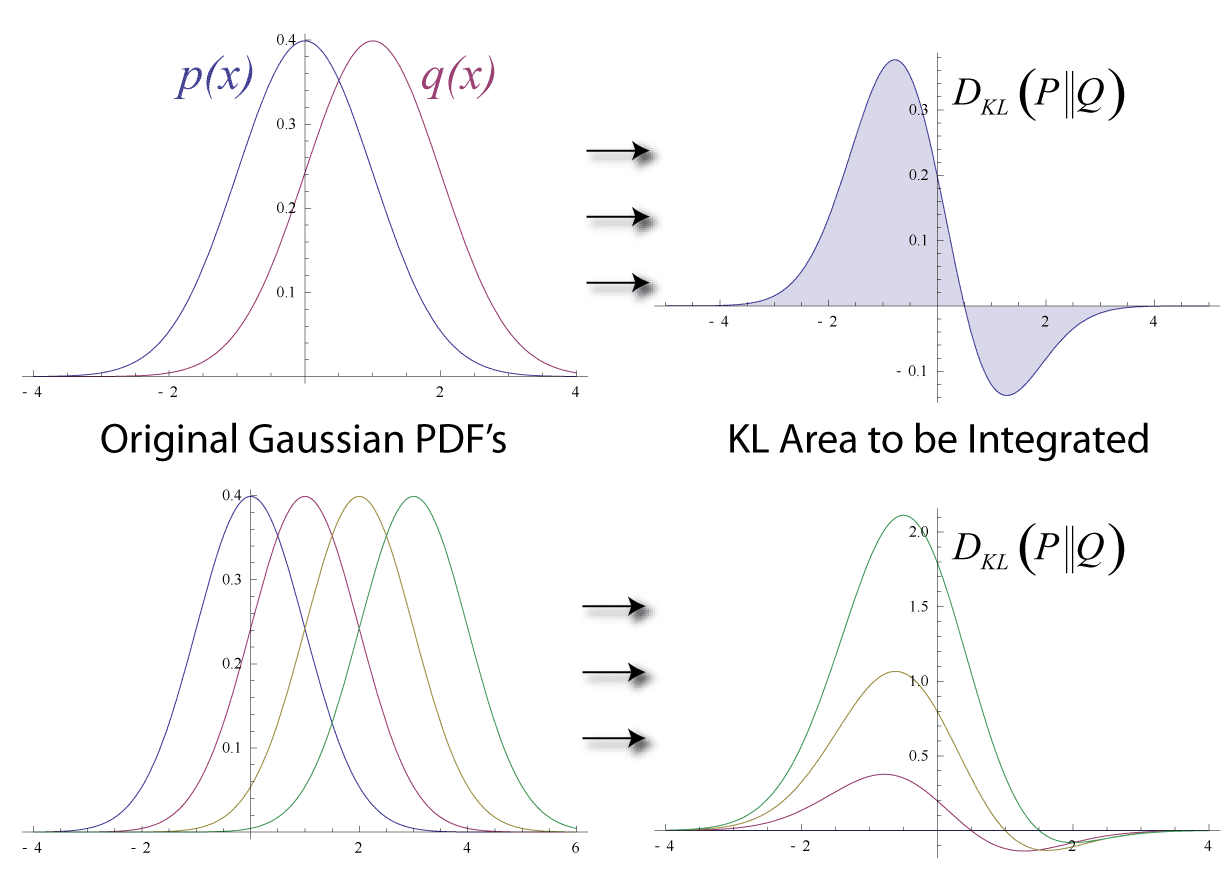
Kullback–Leibler Divergence
In mathematical statistics, the Kullback–Leibler (KL) divergence (also called relative entropy and I-divergence), denoted D_\text(P \parallel Q), is a type of statistical distance: a measure of how much a model probability distribution is different from a true probability distribution . Mathematically, it is defined as D_\text(P \parallel Q) = \sum_ P(x) \, \log \frac\text A simple interpretation of the KL divergence of from is the expected excess surprise from using as a model instead of when the actual distribution is . While it is a measure of how different two distributions are and is thus a distance in some sense, it is not actually a metric, which is the most familiar and formal type of distance. In particular, it is not symmetric in the two distributions (in contrast to variation of information), and does not satisfy the triangle inequality. Instead, in terms of information geometry, it is a type of divergence, a generalization of squared distance, and for cer ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |