|
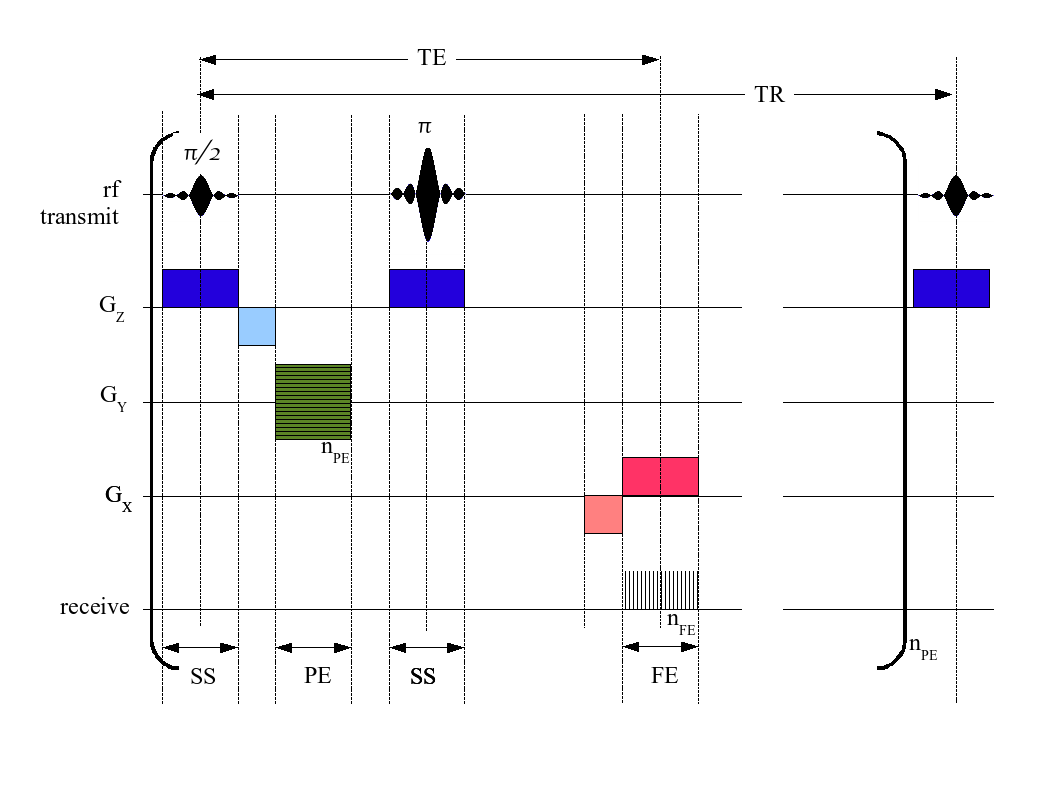
K-space (magnetic Resonance Imaging)
In magnetic resonance imaging (MRI), the ''k''-space or ''reciprocal space'' (a mathematical space of spatial frequencies) is obtained as the 2D or 3D Fourier transform of the image measured. It was introduced in 1979 by Likes and in 1983 by Ljunggren and Twieg. In Physics of magnetic resonance imaging, MRI physics, complex values are sampled in ''k''-space during an MR measurement in a premeditated scheme controlled by a ''MRI sequence, pulse sequence'', i.e. an accurately timed sequence of radiofrequency and gradient pulses. In practice, ''k''-space often refers to the ''temporary image space'', usually a matrix, in which data from digitized MR signals are stored during data acquisition. When ''k''-space is full (at the end of the scan) the data are mathematically processed to produce a final image. Thus ''k''-space holds ''raw'' data before ''reconstruction''. It can be formulated by defining ''wave vectors'' k_\mathrm and k_\mathrm for "frequency encoding" (FE) and "phase enc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Magnetic Resonance Imaging
Magnetic resonance imaging (MRI) is a medical imaging technique used in radiology to generate pictures of the anatomy and the physiological processes inside the body. MRI scanners use strong magnetic fields, magnetic field gradients, and radio waves to form images of the organs in the body. MRI does not involve X-rays or the use of ionizing radiation, which distinguishes it from computed tomography (CT) and positron emission tomography (PET) scans. MRI is a medical application of nuclear magnetic resonance (NMR) which can also be used for imaging in other NMR applications, such as NMR spectroscopy. MRI is widely used in hospitals and clinics for medical diagnosis, staging and follow-up of disease. Compared to CT, MRI provides better contrast in images of soft tissues, e.g. in the brain or abdomen. However, it may be perceived as less comfortable by patients, due to the usually longer and louder measurements with the subject in a long, confining tube, although ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Reciprocal Space
Reciprocal lattice is a concept associated with solids with translational symmetry which plays a major role in many areas such as X-ray diffraction, X-ray and Electron diffraction, electron diffraction as well as the Electronic band structure, energies of electrons in a solid. It emerges from the Fourier transform of the lattice (group), lattice associated with the arrangement of the atoms. The ''direct lattice'' or ''real lattice'' is a periodic function in Space (physics), physical space, such as a crystal system (usually a Bravais lattice). The reciprocal lattice exists in the mathematical space of spatial frequencies or wavenumbers ''k'', known as reciprocal space or ''k'' space; it is the dual of physical space considered as a vector space. In other words, the reciprocal lattice is the sublattice which Dual lattice, is dual to the direct lattice. The reciprocal lattice is the set of all vector (geometric), vectors \mathbf_m, that are wave vector, wavevectors k of plane waves ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spatial Frequencies
In mathematics, physics, and engineering, spatial frequency is a characteristic of any structure that is periodic across position in space. The spatial frequency is a measure of how often sinusoidal components (as determined by the Fourier transform) of the structure repeat per unit of distance. The SI unit of spatial frequency is the reciprocal metre (m−1), (11 pages) although cycle (rotational unit), cycles per (c/m) is also common. In image-processing applications, spatial frequen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fourier Transform
In mathematics, the Fourier transform (FT) is an integral transform that takes a function as input then outputs another function that describes the extent to which various frequencies are present in the original function. The output of the transform is a complex-valued function of frequency. The term ''Fourier transform'' refers to both this complex-valued function and the mathematical operation. When a distinction needs to be made, the output of the operation is sometimes called the frequency domain representation of the original function. The Fourier transform is analogous to decomposing the sound of a musical chord into the intensities of its constituent pitches. Functions that are localized in the time domain have Fourier transforms that are spread out across the frequency domain and vice versa, a phenomenon known as the uncertainty principle. The critical case for this principle is the Gaussian function, of substantial importance in probability theory and statist ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Physics Of Magnetic Resonance Imaging
Magnetic resonance imaging (MRI) is a medical imaging technique mostly used in radiology and nuclear medicine in order to investigate the anatomy and physiology of the body, and to detect pathologies including tumors, inflammation, neurological conditions such as stroke, disorders of muscles and joints, and abnormalities in the heart and blood vessels among other things. Contrast agents may be injected intravenously or into a joint to enhance the image and facilitate diagnosis. Unlike CT and X-ray, MRI uses no ionizing radiation and is, therefore, a safe procedure suitable for diagnosis in children and repeated runs. Patients with specific non-ferromagnetic metal implants, cochlear implants, and cardiac pacemakers nowadays may also have an MRI in spite of effects of the strong magnetic fields. This does not apply on older devices, and details for medical professionals are provided by the device's manufacturer. Certain atomic nuclei are able to absorb and emit radio frequency e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
MRI Sequence
An MRI pulse sequence in magnetic resonance imaging (MRI) is a particular setting of pulse sequences and pulsed field gradients, resulting in a particular image appearance. A multiparametric MRI is a combination of two or more sequences, and/or including Magnetic resonance imaging#Other specialized configurations, other specialized MRI configurations such as In vivo magnetic resonance spectroscopy, spectroscopy. Spin echo T1 and T2 Each tissue returns to its equilibrium state after excitation by the independent relaxation processes of T1 (Spin–lattice relaxation, spin-lattice; that is, magnetization in the same direction as the static magnetic field) and T2 (Spin-spin relaxation time, spin-spin; transverse to the static magnetic field). To create a T1-weighted image, magnetization is allowed to recover before measuring the MR signal by changing the repetition time (TR). This image weighting is useful for assessing the cerebral cortex, identifying fatty tissue, characteriz ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wave Vector
In physics, a wave vector (or wavevector) is a vector used in describing a wave, with a typical unit being cycle per metre. It has a magnitude and direction. Its magnitude is the wavenumber of the wave (inversely proportional to the wavelength), and its direction is perpendicular to the wavefront. In isotropic media, this is also the direction of wave propagation. A closely related vector is the angular wave vector (or angular wavevector), with a typical unit being radian per metre. The wave vector and angular wave vector are related by a fixed constant of proportionality, 2 radians per cycle. It is common in several fields of physics to refer to the angular wave vector simply as the ''wave vector'', in contrast to, for example, crystallography. It is also common to use the symbol for whichever is in use. In the context of special relativity, a '' wave four-vector'' can be defined, combining the (angular) wave vector and (angular) frequency. Definition The terms ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gyromagnetic Ratio
In physics, the gyromagnetic ratio (also sometimes known as the magnetogyric ratio in other disciplines) of a particle or system is the ratio of its magnetic moment to its angular momentum, and it is often denoted by the symbol , gamma. Its SI unit is the reciprocal second per tesla (s−1⋅T−1) or, equivalently, the coulomb per kilogram (C⋅kg−1). The -factor of a particle is a related dimensionless value of the system, derived as the ratio of its gyromagnetic ratio to that which would be classically expected from a rigid body of which the mass and charge are distributed identically, and for which total mass and charge are the same as that of the system. For a classical rotating body Consider a nonconductive charged body rotating about an axis of symmetry. According to the laws of classical physics, it has both a magnetic dipole moment due to the movement of charge and an angular momentum due to the movement of mass arising from its rotation. It can be shown that as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fourier Transform
In mathematics, the Fourier transform (FT) is an integral transform that takes a function as input then outputs another function that describes the extent to which various frequencies are present in the original function. The output of the transform is a complex-valued function of frequency. The term ''Fourier transform'' refers to both this complex-valued function and the mathematical operation. When a distinction needs to be made, the output of the operation is sometimes called the frequency domain representation of the original function. The Fourier transform is analogous to decomposing the sound of a musical chord into the intensities of its constituent pitches. Functions that are localized in the time domain have Fourier transforms that are spread out across the frequency domain and vice versa, a phenomenon known as the uncertainty principle. The critical case for this principle is the Gaussian function, of substantial importance in probability theory and statist ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fourier Analysis
In mathematics, Fourier analysis () is the study of the way general functions may be represented or approximated by sums of simpler trigonometric functions. Fourier analysis grew from the study of Fourier series, and is named after Joseph Fourier, who showed that representing a function as a sum of trigonometric functions greatly simplifies the study of heat transfer. The subject of Fourier analysis encompasses a vast spectrum of mathematics. In the sciences and engineering, the process of decomposing a function into oscillatory components is often called Fourier analysis, while the operation of rebuilding the function from these pieces is known as Fourier synthesis. For example, determining what component frequencies are present in a musical note would involve computing the Fourier transform of a sampled musical note. One could then re-synthesize the same sound by including the frequency components as revealed in the Fourier analysis. In mathematics, the term ''Fourier an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Signal-to-noise Ratio (imaging)
Signal-to-noise ratio (SNR) is used in imaging to characterize image quality. The sensitivity of a (digital or film) imaging system is typically described in the terms of the signal level that yields a threshold level of SNR. Industry standards define sensitivity in terms of the ISO film speed equivalent, using SNR thresholds (at average scene luminance) of 40:1 for "excellent" image quality and 10:1 for "acceptable" image quality. SNR is sometimes quantified in decibels (dB) of signal power relative to noise power, though in the imaging field the concept of "power" is sometimes taken to be the power of a voltage signal proportional to optical power; so a 20 dB SNR may mean either 10:1 or 100:1 optical power, depending on which definition is in use. Definition of SNR Traditionally, SNR is defined to be the ratio of the average signal value \mu_\mathrm to the standard deviation of the signal \sigma_\mathrm: : \mathrm = \frac when the signal is an optical intensity, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |