|
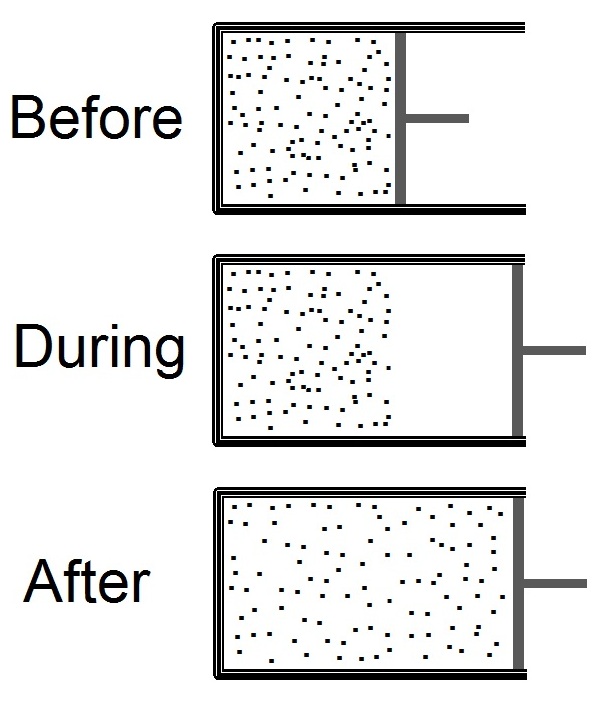
Joule Expansion
The Joule expansion (also called free expansion) is an irreversible process in thermodynamics in which a volume of gas is kept in one side of a thermally isolated container (via a small partition), with the other side of the container being evacuated. The partition between the two parts of the container is then opened, and the gas fills the whole container. The Joule expansion, treated as a thought experiment involving ideal gases, is a useful exercise in classical thermodynamics. It provides a convenient example for calculating changes in thermodynamic quantities, including the resulting increase in entropy of the universe (entropy production) that results from this inherently irreversible process. An actual Joule expansion experiment necessarily involves real gases; the temperature change in such a process provides a measure of intermolecular forces. This type of expansion is named after James Prescott Joule who used this expansion, in 1845, in his study for the mechanical equ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Thermodynamic System
A thermodynamic system is a body of matter and/or radiation, confined in space by walls, with defined permeabilities, which separate it from its surroundings. The surroundings may include other thermodynamic systems, or physical systems that are not thermodynamic systems. A wall of a thermodynamic system may be purely notional, when it is described as being 'permeable' to all matter, all radiation, and all forces. A state of a thermodynamic system can be fully described in several different ways, by several different sets of thermodynamic state variables. A widely used distinction is between ''isolated'', ''closed'', and ''open'' thermodynamic systems. An isolated thermodynamic system has walls that are non-conductive of heat and perfectly reflective of all radiation, that are rigid and immovable, and that are impermeable to all forms of matter and all forces. (Some writers use the word 'closed' when here the word 'isolated' is being used.) A closed thermodynamic system is c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Adiabatic Expansion
In thermodynamics, an adiabatic process (Greek: ''adiábatos'', "impassable") is a type of thermodynamic process that occurs without transferring heat or mass between the thermodynamic system and its environment. Unlike an isothermal process, an adiabatic process transfers energy to the surroundings only as work.. A translation may be founhere. Also a mostly reliabltranslation is to be foundin As a key concept in thermodynamics, the adiabatic process supports the theory that explains the first law of thermodynamics. Some chemical and physical processes occur too rapidly for energy to enter or leave the system as heat, allowing a convenient "adiabatic approximation".Bailyn, M. (1994), pp. 52–53. For example, the adiabatic flame temperature uses this approximation to calculate the upper limit of flame temperature by assuming combustion loses no heat to its surroundings. In meteorology and oceanography, adiabatic cooling produces condensation of moisture or salinity, oversatura ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fundamental Thermodynamic Relation
In thermodynamics, the fundamental thermodynamic relation are four fundamental equations which demonstrate how four important thermodynamic quantities depend on variables that can be controlled and measured experimentally. Thus, they are essentially equations of state, and using the fundamental equations, experimental data can be used to determine sought-after quantities like ''G'' or ''H''. The relation is generally expressed as a microscopic change in internal energy in terms of microscopic changes in entropy, and volume (thermodynamics), volume for a closed system in thermal equilibrium in the following way. :\mathrmU= T\,\mathrmS - P\,\mathrmV\, Here, ''U'' is internal energy, ''T'' is absolute temperature, ''S'' is entropy, ''P'' is pressure, and ''V'' is volume. This is only one expression of the fundamental thermodynamic relation. It may be expressed in other ways, using different variables (e.g. using thermodynamic potentials). For example, the fundamental relation may ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sackur–Tetrode Equation
The Sackur–Tetrode equation is an expression for the entropy of a monatomic ideal gas. It is named for Hugo Martin Tetrode (1895–1931) and Otto Sackur (1880–1914), who developed it independently as a solution of Boltzmann's gas statistics and entropy equations, at about the same time in 1912. Formula The Sackur–Tetrode equation expresses the entropy S of a monatomic ideal gas in terms of its thermodynamic state—specifically, its volume V, internal energy U, and the number of particles N: : \frac = \ln \left \frac VN \left(\frac\frac UN\right)^\right , where k_\mathrm is the Boltzmann constant, m is the mass of a gas particle and h is the Planck constant. The equation can also be expressed in terms of the thermal wavelength \Lambda: : \frac = \ln\left(\frac\right)+\frac , For a derivation of the Sackur–Tetrode equation, see the Gibbs paradox. For the constraints placed upon the entropy of an ideal gas by thermodynamics alone, see the ideal gas article. The above ex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Monatomic Gas
In physics and chemistry, "monatomic" is a combination of the words "mono" and "atomic", and means "single atom". It is usually applied to gases: a monatomic gas is a gas in which atoms are not bound to each other. Examples at standard conditions of temperature and pressure include all the noble gases (helium, neon, argon, krypton, xenon, and radon), though all chemical elements will be monatomic in the gas phase at sufficiently high temperature (or very low pressure). The thermodynamic behavior of a monatomic gas is much simpler when compared to polyatomic gases because it is free of any rotational or vibrational energy. Noble gases The only chemical elements that are stable single atoms (so they are not molecules) at standard temperature and pressure (STP) are the noble gases. These are helium, neon, argon, krypton, xenon, and radon. Noble gases have a full outer valence shell making them rather non-reactive species. While these elements have been described historically as co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isothermal Process
In thermodynamics, an isothermal process is a type of thermodynamic process in which the temperature ''T'' of a system remains constant: Δ''T'' = 0. This typically occurs when a system is in contact with an outside thermal reservoir, and a change in the system occurs slowly enough to allow the system to be continuously adjusted to the temperature of the reservoir through heat exchange (see quasi-equilibrium). In contrast, an ''adiabatic process'' is where a system exchanges no heat with its surroundings (''Q'' = 0). Simply, we can say that in an isothermal process * T = \text * \Delta T = 0 * dT = 0 * For ideal gases only, internal energy \Delta U = 0 while in adiabatic processes: * Q = 0. Etymology The adjective "isothermal" is derived from the Greek words "ἴσος" ("isos") meaning "equal" and "θέρμη" ("therme") meaning "heat". Examples Isothermal processes can occur in any kind of system that has some means of regulating the temperature, including ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Function Of State
In the thermodynamics of equilibrium, a state function, function of state, or point function for a thermodynamic system is a mathematical function relating several state variables or state quantities (that describe equilibrium states of a system) that depend only on the current equilibrium thermodynamic state of the system (e.g. gas, liquid, solid, crystal, or emulsion), not the path which the system has taken to reach that state. A state function describes equilibrium states of a system, thus also describing the type of system. A state variable is typically a state function so the determination of other state variable values at an equilibrium state also determines the value of the state variable as the state function at that state. The ideal gas law is a good example. In this law, one state variable (e.g., pressure, volume, temperature, or the amount of substance in a gaseous equilibrium system) is a function of other state variables so is regarded as a state function. A state fu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lennard-Jones Potential
The Lennard-Jones potential (also termed the LJ potential or 12-6 potential) is an intermolecular pair potential. Out of all the intermolecular potentials, the Lennard-Jones potential is probably the one that has been the most extensively studied. It is considered an archetype model for simple yet realistic intermolecular interactions. The Lennard-Jones potential models soft repulsive and attractive ( van der Waals) interactions. Hence, the Lennard-Jones potential describes electronically neutral atoms or molecules. It is named after John Lennard-Jones. The commonly used expression for the Lennard-Jones potential is V_\text(r) = 4\varepsilon \left \left(\frac\right)^ - \left(\frac\right)^6 \right, where r is the distance between two interacting particles, \varepsilon is the depth of the potential well (usually referred to as 'dispersion energy'), and \sigma is the distance at which the particle-particle potential energy V is zero (often referred to as 'size of the particle'). The ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Internal Energy
The internal energy of a thermodynamic system is the total energy contained within it. It is the energy necessary to create or prepare the system in its given internal state, and includes the contributions of potential energy and internal kinetic energy. It keeps account of the gains and losses of energy of the system that are due to changes in its internal state. It does not include the kinetic energy of motion of the system as a whole, or any external energies from surrounding force fields. The internal energy of an isolated system is constant, which is expressed as the law of conservation of energy, a foundation of the first law of thermodynamics. The internal energy is an extensive property. The internal energy cannot be measured directly and knowledge of all its components is rarely interesting, such as the static rest mass energy of its constituent matter. Thermodynamics is chiefly concerned only with ''changes'' in the internal energy, not with its absolute value. Instea ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ideal Gas Constant
The molar gas constant (also known as the gas constant, universal gas constant, or ideal gas constant) is denoted by the symbol or . It is the molar equivalent to the Boltzmann constant, expressed in units of energy per temperature increment per amount of substance, i.e. the pressure–volume product, rather than energy per temperature increment per ''particle''. The constant is also a combination of the constants from Boyle's law, Charles's law, Avogadro's law, and Gay-Lussac's law. It is a physical constant that is featured in many fundamental equations in the physical sciences, such as the ideal gas law, the Arrhenius equation, and the Nernst equation. The gas constant is the constant of proportionality that relates the energy scale in physics to the temperature scale and the scale used for amount of substance. Thus, the value of the gas constant ultimately derives from historical decisions and accidents in the setting of units of energy, temperature and amount of substance ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ideal Gas Law
The ideal gas law, also called the general gas equation, is the equation of state of a hypothetical ideal gas. It is a good approximation of the behavior of many gases under many conditions, although it has several limitations. It was first stated by Benoît Paul Émile Clapeyron in 1834 as a combination of the empirical Boyle's law, Charles's law, Avogadro's law, and Gay-Lussac's law. The ideal gas law is often written in an empirical form: pV = nRT where p, V and T are the pressure, volume and temperature; n is the amount of substance; and R is the ideal gas constant. It can also be derived from the microscopic kinetic theory, as was achieved (apparently independently) by August Krönig in 1856 and Rudolf Clausius in 1857. Equation The state of an amount of gas is determined by its pressure, volume, and temperature. The modern form of the equation relates these simply in two main forms. The temperature used in the equation of state is an absolute temperature: the appropria ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |