|
John Penn Mayberry
John Penn Mayberry (18 November 1939 – 19 August 2016) was an American mathematical philosopher and creator of a distinctive Aristotelian philosophy of mathematics to which he gave expression in his book ''The Foundations of Mathematics in the Theory of Sets''. Following completion of a Ph.D. at Illinois under the supervision of Gaisi Takeuti, he took up, in 1966, a position in the mathematics department of the University of Bristol The University of Bristol is a public university, public research university in Bristol, England. It received its royal charter in 1909, although it can trace its roots to a Merchant Venturers' school founded in 1595 and University College, Br .... He remained there until his retirement in 2004 as a Reader in Mathematics. Philosophical work Mayberry's philosophy rejects the Philosophy of mathematics#Platonism, Platonic tradition, which holds mathematics to be a transcendental science concerned with discovering truths about immaterial, but in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Aristotelian Realism
In the philosophy of mathematics, Aristotelian realism holds that mathematics studies properties such as symmetry, continuity and order that can be immanently realized in the physical world (or in any other world there might be). It contrasts with Platonism in holding that the objects of mathematics, such as numbers, do not exist in an "abstract" world but can be physically realized. It contrasts with nominalism, fictionalism, and logicism in holding that mathematics is not about mere names or methods of inference or calculation but about certain real aspects of the world. Aristotelian realists emphasize applied mathematics, especially mathematical modeling, rather than pure mathematics as philosophically most important. argues that "Aristotelian realism allows mathematical facts to be explainers in distinctively mathematical explanations" in science as mathematical facts are themselves about the physical world. Paul Thagard describes Aristotelian realism as "the current philoso ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jacob Klein (philosopher)
Jacob Klein (March 3, 1899 – July 16, 1978) was a Russian-American philosopher and interpreter of Plato, who worked extensively on the nature and historical origin of modern symbolic mathematics. Biography Klein was born in Libava, Russian Empire. He studied at Berlin and Marburg, where he received his Ph.D. in 1922. A student of Nicolai Hartmann, Martin Heidegger, and Edmund Husserl, he later taught at St. John's College in Annapolis, Maryland from 1938 until his death. He served as dean from 1949 to 1958. Klein was affectionately known as Jasha (pronounced "Yasha"). He was one of the world's preeminent interpreters of Plato and the Platonic tradition. As one of many Jewish scholars who were no longer safe in Europe, he fled the Nazis. He was a friend of fellow émigré and German-American philosopher Leo Strauss. Of Klein's first book ''Greek Mathematical Thought and the Origin of Algebra'', Strauss said: The work is much more than a historical study. But even if we take ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Zermelo–Fraenkel Set Theory
In set theory, Zermelo–Fraenkel set theory, named after mathematicians Ernst Zermelo and Abraham Fraenkel, is an axiomatic system that was proposed in the early twentieth century in order to formulate a theory of sets free of paradoxes such as Russell's paradox. Today, Zermelo–Fraenkel set theory, with the historically controversial axiom of choice (AC) included, is the standard form of axiomatic set theory and as such is the most common foundation of mathematics. Zermelo–Fraenkel set theory with the axiom of choice included is abbreviated ZFC, where C stands for "choice", and ZF refers to the axioms of Zermelo–Fraenkel set theory with the axiom of choice excluded. Informally, Zermelo–Fraenkel set theory is intended to formalize a single primitive notion, that of a hereditary well-founded set, so that all entities in the universe of discourse are such sets. Thus the axioms of Zermelo–Fraenkel set theory refer only to pure sets and prevent its models fr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Recursive Definition
In mathematics and computer science, a recursive definition, or inductive definition, is used to define the elements in a set in terms of other elements in the set ( Aczel 1977:740ff). Some examples of recursively definable objects include factorials, natural numbers, Fibonacci numbers, and the Cantor ternary set. A recursive definition of a function defines values of the function for some inputs in terms of the values of the same function for other (usually smaller) inputs. For example, the factorial function is defined by the rules :\begin & 0! = 1. \\ & (n+1)! = (n+1) \cdot n!. \end This definition is valid for each natural number , because the recursion eventually reaches the base case of 0. The definition may also be thought of as giving a procedure for computing the value of the function , starting from and proceeding onwards with etc. The recursion theorem states that such a definition indeed defines a function that is unique. The proof uses mathematic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Induction
Mathematical induction is a method for mathematical proof, proving that a statement P(n) is true for every natural number n, that is, that the infinitely many cases P(0), P(1), P(2), P(3), \dots all hold. This is done by first proving a simple case, then also showing that if we assume the claim is true for a given case, then the next case is also true. Informal metaphors help to explain this technique, such as falling dominoes or climbing a ladder: A proof by induction consists of two cases. The first, the base case, proves the statement for n = 0 without assuming any knowledge of other cases. The second case, the induction step, proves that ''if'' the statement holds for any given case n = k, ''then'' it must also hold for the next case n = k + 1. These two steps establish that the statement holds for every natural number n. The base case does not necessarily begin with n = 0, but often with n = 1, and possibly with any fixed natural number n = N, establishing the trut ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Field (mathematics)
In mathematics, a field is a set (mathematics), set on which addition, subtraction, multiplication, and division (mathematics), division are defined and behave as the corresponding operations on rational number, rational and real numbers. A field is thus a fundamental algebraic structure which is widely used in algebra, number theory, and many other areas of mathematics. The best known fields are the field of rational numbers, the field of real numbers and the field of complex numbers. Many other fields, such as field of rational functions, fields of rational functions, algebraic function fields, algebraic number fields, and p-adic number, ''p''-adic fields are commonly used and studied in mathematics, particularly in number theory and algebraic geometry. Most cryptographic protocols rely on finite fields, i.e., fields with finitely many element (set), elements. The theory of fields proves that angle trisection and squaring the circle cannot be done with a compass and straighte ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Peacock's Principle
George Peacock FRS (9 April 1791 – 8 November 1858) was an English mathematician and Anglican cleric. He founded what has been called the British algebra of logic. Early life Peacock was born on 9 April 1791 at Thornton Hall, Denton, near Darlington, County Durham. His father, Thomas Peacock, was a priest of the Church of England, incumbent and for 50 years curate of the parish of Denton, where he also kept a school. In early life, Peacock did not show any precocity of genius. He was more remarkable for daring feats of climbing than for any special attachment to study. Initially, he received his elementary education from his father and then at Sedbergh School, and at 17 years of age, he was sent to Richmond School under James Tate, a graduate of Cambridge University. At this school he distinguished himself greatly both in classics and in the rather elementary mathematics then required for entrance at Cambridge. In 1809 he became a student of Trinity College, Cambridge. I ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Intuitionism
In the philosophy of mathematics, intuitionism, or neointuitionism (opposed to preintuitionism), is an approach where mathematics is considered to be purely the result of the constructive mental activity of humans rather than the discovery of fundamental principles claimed to exist in an objective reality. That is, logic and mathematics are not considered analytic activities wherein deep properties of objective reality are revealed and applied, but are instead considered the application of internally consistent methods used to realize more complex mental constructs, regardless of their possible independent existence in an objective reality. Truth and proof The fundamental distinguishing characteristic of intuitionism is its interpretation of what it means for a mathematical statement to be true. In Luitzen Egbertus Jan Brouwer, Brouwer's original intuitionism, the truth of a mathematical statement is a subjective claim: a mathematical statement corresponds to a mental construc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Henri Poincaré
Jules Henri Poincaré (, ; ; 29 April 185417 July 1912) was a French mathematician, Theoretical physics, theoretical physicist, engineer, and philosophy of science, philosopher of science. He is often described as a polymath, and in mathematics as "The Last Universalist", since he excelled in all fields of the discipline as it existed during his lifetime. He has further been called "the Carl Friedrich Gauss, Gauss of History of mathematics, modern mathematics". Due to his success in science, along with his influence and philosophy, he has been called "the philosopher par excellence of modern science". As a mathematician and physicist, he made many original fundamental contributions to Pure mathematics, pure and applied mathematics, mathematical physics, and celestial mechanics. In his research on the three-body problem, Poincaré became the first person to discover a chaotic deterministic system which laid the foundations of modern chaos theory. Poincaré is regarded as the cr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Richard Dedekind
Julius Wilhelm Richard Dedekind (; ; 6 October 1831 – 12 February 1916) was a German mathematician who made important contributions to number theory, abstract algebra (particularly ring theory), and the axiomatic foundations of arithmetic. His best known contribution is the definition of real numbers through the notion of Dedekind cut. He is also considered a pioneer in the development of modern set theory and of the philosophy of mathematics known as ''logicism''. Life Dedekind's father was Julius Levin Ulrich Dedekind, an administrator of Collegium Carolinum in Braunschweig. His mother was Caroline Henriette Dedekind (née Emperius), the daughter of a professor at the Collegium. Richard Dedekind had three older siblings. As an adult, he never used the names Julius Wilhelm. He was born in Braunschweig (often called "Brunswick" in English), which is where he lived most of his life and died. His body rests at Braunschweig Main Cemetery. He first attended the Collegium Carol ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
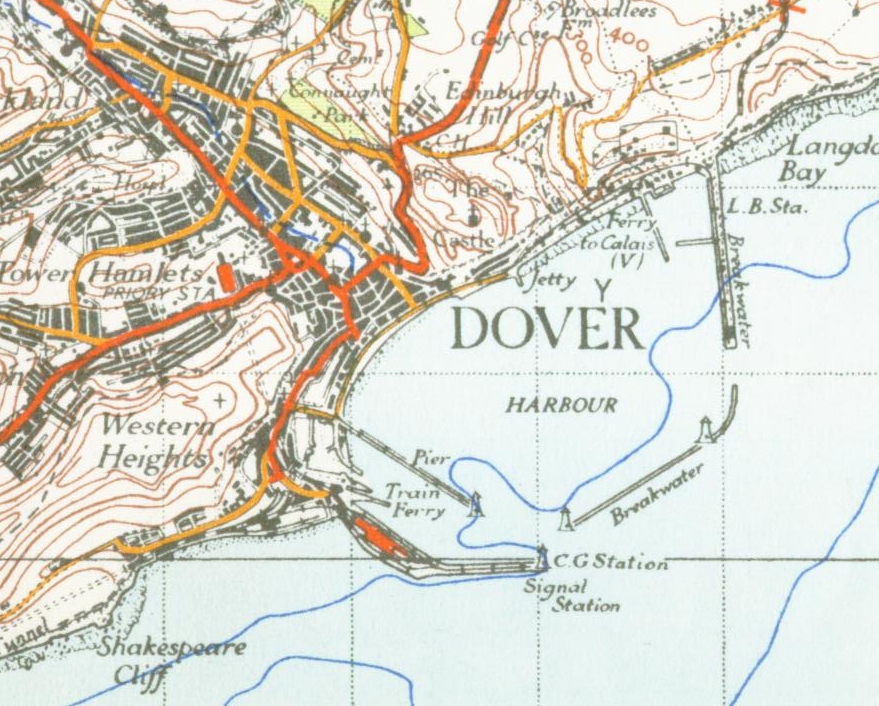
Dover
Dover ( ) is a town and major ferry port in Kent, southeast England. It faces France across the Strait of Dover, the narrowest part of the English Channel at from Cap Gris Nez in France. It lies southeast of Canterbury and east of Maidstone. The town is the administrative centre of the Dover District and home of the Port of Dover. Archaeological finds have revealed that the area has always been a focus for peoples entering and leaving Great Britain, Britain. The name derives from the River Dour that flows through it. In recent times the town has undergone transformations with a high-speed rail link to London, new retail in town with St James' area opened in 2018, and a revamped promenade and beachfront. This followed in 2019, with a new 500m Pier to the west of the Harbour, and new Marina unveiled as part of a £330m investment in the area. It has also been a point of destination for many English Channel migrant crossings (2018-present), illegal migrant crossings. The Port ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cambridge University Press
Cambridge University Press was the university press of the University of Cambridge. Granted a letters patent by King Henry VIII in 1534, it was the oldest university press in the world. Cambridge University Press merged with Cambridge Assessment to form Cambridge University Press and Assessment under Queen Elizabeth II's approval in August 2021. With a global sales presence, publishing hubs, and offices in more than 40 countries, it published over 50,000 titles by authors from over 100 countries. Its publications include more than 420 academic journals, monographs, reference works, school and university textbooks, and English language teaching and learning publications. It also published Bibles, runs a bookshop in Cambridge, sells through Amazon, and has a conference venues business in Cambridge at the Pitt Building and the Sir Geoffrey Cass Sports and Social Centre. It also served as the King's Printer. Cambridge University Press, as part of the University of Cambridge, was a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |