|
Ionic Coulomb Blockade
Ionic Coulomb blockade (ICB) is an electrostatic phenomenon predicted by M. Krems and Massimiliano Di Ventra (UC San Diego) that appears in ionic transport through Mesoscopic physics, mesoscopic electro-diffusive systems (artificial nanopores and biological ion channels) and manifests itself as oscillatory dependences of the conductance on the fixed charge Q_ in the pore ( or on the external voltage V, or on the bulk concentration c_). ICB represents an ion-related counterpart of the better-known electronic Coulomb blockade (ECB) that is observed in quantum dots. Both ICB and ECB arise from Charge quantization, quantisation of the electric charge and from an electrostatic exclusion principle and they share in common a number of effects and underlying physical mechanisms. ICB provides some specific effects related to the existence of ions of different charge q=ze (different in both sign and value) where integer z is ion valence and e is the elementary charge, in contrast to the singl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Phenomenon
A phenomenon ( phenomena), sometimes spelled phaenomenon, is an observable Event (philosophy), event. The term came into its modern Philosophy, philosophical usage through Immanuel Kant, who contrasted it with the noumenon, which ''cannot'' be directly observed. Kant was heavily influenced by Gottfried Wilhelm Leibniz in this part of his philosophy, in which phenomenon and noumenon serve as interrelated technical terms. Far predating this, the Ancient Greek Philosophy, ancient Greek Pyrrhonism, Pyrrhonist philosopher Sextus Empiricus also used ''phenomenon'' and ''noumenon'' as interrelated technical terms. Common usage In popular usage, a ''phenomenon'' often refers to an extraordinary, unusual or notable event. According to the ''Dictionary of Visual Discourse'':In ordinary language 'phenomenon/phenomena' refer to any occurrence worthy of note and investigation, typically an untoward or unusual event, person or fact that is of special significance or otherwise notable. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Langevin Equation
In physics, a Langevin equation (named after Paul Langevin) is a stochastic differential equation describing how a system evolves when subjected to a combination of deterministic and fluctuating ("random") forces. The dependent variables in a Langevin equation typically are collective (macroscopic) variables changing only slowly in comparison to the other (microscopic) variables of the system. The fast (microscopic) variables are responsible for the stochastic nature of the Langevin equation. One application is to Brownian motion, which models the fluctuating motion of a small particle in a fluid. Brownian motion as a prototype The original Langevin equation describes Brownian motion, the apparently random movement of a particle in a fluid due to collisions with the molecules of the fluid, m\frac=-\lambda \mathbf+\boldsymbol\left( t\right). Here, \mathbf is the velocity of the particle, \lambda is its damping coefficient, and m is its mass. The force acting on the particle is w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Proceedings Of The Cambridge Philosophical Society
''Mathematical Proceedings of the Cambridge Philosophical Society'' is a mathematical journal published by Cambridge University Press for the Cambridge Philosophical Society. It aims to publish original research papers from a wide range of pure and applied mathematics. The journal, titled ''Proceedings of the Cambridge Philosophical Society'' before 1975, has been published since 1843. Abstracting and indexing The journal is abstracted and indexed in *MathSciNet *Science Citation Index Expanded *Scopus *ZbMATH Open See also *Cambridge Philosophical Society The Cambridge Philosophical Society (CPS) is a scientific society at the University of Cambridge. It was founded in 1819. The name derives from the medieval use of the word philosophy to denote any research undertaken outside the fields of law ... External linksofficial website References Academic journals associated with learned and professional societies Cambridge University Press academic journals Mathematics e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Langmuir Isotherm
The Langmuir adsorption model explains adsorption by assuming an adsorbate behaves as an ideal gas at isothermal conditions. According to the model, adsorption and desorption are reversible processes. This model even explains the effect of pressure; ''i.e.'', at these conditions the adsorbate's partial pressure p_A is related to its volume adsorbed onto a solid adsorbent. The adsorbent, as indicated in the figure, is assumed to be an ideal solid surface composed of a series of distinct sites capable of binding the adsorbate. The adsorbate binding is treated as a chemical reaction between the adsorbate gaseous molecule A_\text and an empty sorption site . This reaction yields an adsorbed species A_\text with an associated equilibrium constant K_\text: : A_ + S A_. From these basic hypotheses the mathematical formulation of the Langmuir adsorption isotherm can be derived in various independent and complementary ways: by the kinetics, the thermodynamics, and the statistical mech ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
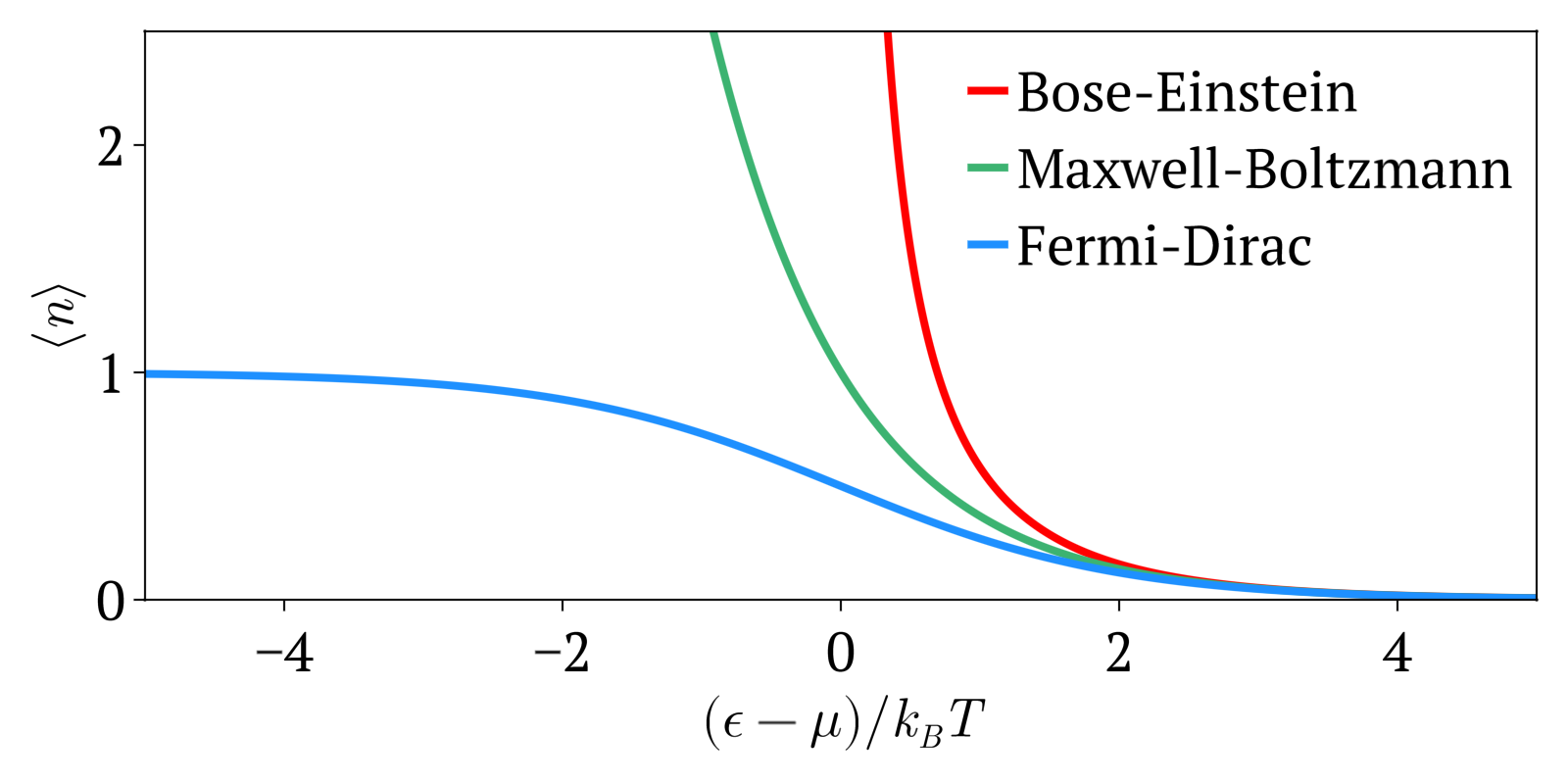
Fermi–Dirac Statistics
Fermi–Dirac statistics is a type of quantum statistics that applies to the physics of a system consisting of many non-interacting, identical particles that obey the Pauli exclusion principle. A result is the Fermi–Dirac distribution of particles over energy states. It is named after Enrico Fermi and Paul Dirac, each of whom derived the distribution independently in 1926. Fermi–Dirac statistics is a part of the field of statistical mechanics and uses the principles of quantum mechanics. Fermi–Dirac statistics applies to identical and indistinguishable particles with half-integer spin (1/2, 3/2, etc.), called fermions, in thermodynamic equilibrium. For the case of negligible interaction between particles, the system can be described in terms of single-particle energy states. A result is the Fermi–Dirac distribution of particles over these states where no two particles can occupy the same state, which has a considerable effect on the properties of the system. Fermi� ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ca Bands
CA most often refers to: * Canada, a country by ISO 3166-1 alpha-2 code * California, U.S. state by postal abbreviation CA or ca may also refer to: Businesses and organizations Companies * Air China (IATA airline code CA) * CA Technologies, a U.S. software company * Cayman Airways, a Cayman Islands airline * Channel America, a defunct U.S. television network * Coal & Allied, Australian mining company * Continental Airlines, a U.S. airline * Creative Assembly, a PC game developer * Crédit Agricole, a major French bank Government and political * Bureau of Consular Affairs, a division of the U.S. Department of State * Canadian Alliance, a former Canadian political party * Centre Alliance, Australian political party formerly known as Nick Xenophon Team * Citizens' Alliance, a political party in Trinidad and Tobago * Combined authority, a local government entity in the United Kingdom * Commission on Appointments, a body of the Congress of the Philippines * Conservatives Abroad, ove ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diffusion
Diffusion is the net movement of anything (for example, atoms, ions, molecules, energy) generally from a region of higher concentration to a region of lower concentration. Diffusion is driven by a gradient in Gibbs free energy or chemical potential. It is possible to diffuse "uphill" from a region of lower concentration to a region of higher concentration, as in spinodal decomposition. Diffusion is a stochastic process due to the inherent randomness of the diffusing entity and can be used to model many real-life stochastic scenarios. Therefore, diffusion and the corresponding mathematical models are used in several fields beyond physics, such as statistics, probability theory, information theory, neural networks, finance, and marketing. The concept of diffusion is widely used in many fields, including physics (Molecular diffusion, particle diffusion), chemistry, biology, sociology, economics, statistics, data science, and finance (diffusion of people, ideas, data and price v ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coulomb Gap
First introduced by M. Pollak, the Coulomb gap is a soft gap in the single-particle density of states (DOS) of a system of interacting localized electrons. Due to the long-range Coulomb interactions, the single-particle DOS vanishes at the chemical potential, at low enough temperatures, such that thermal excitations do not wash out the gap. Theory At zero temperature, a classical treatment of a system gives an upper bound for the DOS near the Fermi energy, first suggested by Efros and Shklovskii. The argument is as follows: Let us look at the ground state configuration of the system. Defining E_i as the energy of an electron at site i , due to the disorder and the Coulomb interaction with all other electrons (we define this both for occupied and unoccupied sites), it is easy to see that the energy needed to move an electron from an occupied site i to an unoccupied site j is given by the expression: :\Delta E=E_j-E_i-e^2/r_ . The subtraction of the last term accounts ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Self-energy
In quantum field theory, the energy that a particle has as a result of changes that it causes in its environment defines its self-energy \Sigma. The self-energy represents the contribution to the particle's energy, or effective mass, due to interactions between the particle and its environment. In electrostatics, the energy required to assemble the charge distribution takes the form of self-energy by bringing in the constituent charges from infinity, where the electric force goes to zero. In a condensed matter context, self-energy is used to describe interaction induced renormalization of quasiparticle mass ( dispersions) and lifetime. Self-energy is especially used to describe electron-electron interactions in Fermi liquids. Another example of self-energy is found in the context of phonon softening due to electron-phonon coupling. Characteristics Mathematically, this energy is equal to the so-called on mass shell value of the proper self-energy ''operator'' (or proper mass ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Excess Chemical Potential
In thermodynamics, the excess chemical potential is defined as the difference between the chemical potential of a given species and that of an ideal gas under the same conditions (in particular, at the same pressure, temperature, and composition). The chemical potential of a particle species i is therefore given by an ideal part and an excess part. :\mu_i=\mu_i^\text+\mu_i^\text Chemical potential of a pure fluid can be estimated by the Widom insertion method. Derivation and Measurement For a system of diameter and volume , at constant temperature , the classical canonical partition function :Q(N,V,T)=\frac\int_^\ldots\int_^ds^\exp \beta U(s^;L)/math> with a scaled coordinate, the free energy is given by: :F(N,V,T)= -k_T\ln Q=-k_T\ln\left(\frac\right)-k_T \ln= :=F_(N,V,T)+F_(N,V,T) Combining the above equation with the definition of chemical potential, :\mu_= \left(\frac\right)_=\left(\frac\right)_, we get the chemical potential of a sufficiently large system from (and th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fermi Level
The Fermi level of a solid-state body is the thermodynamic work required to add one electron to the body. It is a thermodynamic quantity usually denoted by ''μ'' or ''E''F for brevity. The Fermi level does not include the work required to remove the electron from wherever it came from. A precise understanding of the Fermi level—how it relates to electronic band structure in determining electronic properties; how it relates to the voltage and flow of charge in an electronic circuit—is essential to an understanding of solid-state physics. In band structure theory, used in solid state physics to analyze the energy levels in a solid, the Fermi level can be considered to be a hypothetical energy level of an electron, such that at thermodynamic equilibrium this energy level would have a ''50% probability of being occupied at any given time''. The position of the Fermi level in relation to the band energy levels is a crucial factor in determining electrical properties. The Fer ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chemical Potential
In thermodynamics, the chemical potential of a Chemical specie, species is the energy that can be absorbed or released due to a change of the particle number of the given species, e.g. in a chemical reaction or phase transition. The chemical potential of a species in a mixture is defined as the rate of change of Thermodynamic free energy, free energy of a thermodynamic system with respect to the change in the number of atoms or molecules of the species that are added to the system. Thus, it is the partial derivative of the free energy with respect to the amount of the species, all other species' concentrations in the mixture remaining constant. When both temperature and pressure are held constant, and the number of particles is expressed in moles, the chemical potential is the partial Molar concentration, molar Gibbs free energy. At chemical equilibrium or in phase equilibrium, the total sum of the product of chemical potentials and stoichiometric coefficients is zero, as the free en ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |