|
Incomplete Polylogarithm
In mathematics, the incomplete polylogarithm function is related to the polylogarithm function. It is sometimes known as the incomplete Fermi–Dirac integral or the incomplete Bose–Einstein integral. It may be defined by: : \operatorname_s(b,z) = \frac\int_b^\infty \frac~dx. Expanding about z=0 and integrating gives a series representation: : \operatorname_s(b,z) = \sum_^\infty \frac~\frac where Γ(s) is the gamma function and Γ(s,x) is the upper incomplete gamma function In mathematics, the upper and lower incomplete gamma functions are types of special functions which arise as solutions to various mathematical problems such as certain integrals. Their respective names stem from their integral definitions, whic .... Since Γ(s,0)=Γ(s), it follows that: : \operatorname_s(0,z) =\operatorname{Li}_s(z) where Lis(.) is the polylogarithm function. References * GNU Scientific Library - Reference Manual https://www.gnu.org/software/gsl/manual/gsl-r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polylogarithm
In mathematics, the polylogarithm (also known as Jonquière's function, for Alfred Jonquière) is a special function of order and argument . Only for special values of does the polylogarithm reduce to an elementary function such as the natural logarithm or a rational function. In quantum statistics, the polylogarithm function appears as the closed form of integrals of the Fermi–Dirac distribution and the Bose–Einstein distribution, and is also known as the Fermi–Dirac integral or the Bose–Einstein integral. In quantum electrodynamics, polylogarithms of positive integer order arise in the calculation of processes represented by higher-order Feynman diagrams. The polylogarithm function is equivalent to the Hurwitz zeta function — either function can be expressed in terms of the other — and both functions are special cases of the Lerch transcendent. Polylogarithms should not be confused with polylogarithmic functions, nor with the offset logarithmic integra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Incomplete Fermi–Dirac Integral
In mathematics, the incomplete Fermi-Dirac integral, named after Enrico Fermi and Paul Dirac, for an index j and parameter b is given by :\operatorname_j(x,b) \overset \frac \int_b^\infty\! \frac\;\mathrmt Its derivative is :\frac\operatorname_j(x,b) = \operatorname_(x,b) and this derivative relationship may be used to find the value of the incomplete Fermi-Dirac integral for non-positive indices j. This is an alternate definition of the incomplete polylogarithm, since: :\operatorname_j(x,b) = \frac \int_b^\infty\! \frac\;\mathrmt = \frac \int_b^\infty\! \frac\;\mathrmt = -\frac \int_b^\infty\! \frac\;\mathrmt = -\operatorname_(b,-e^x) Which can be used to prove the identity: : \operatorname_j(x,b) = -\sum_^\infty \frac\frace^ where \Gamma(s) is the gamma function and \Gamma(s,y) is the upper incomplete gamma function. Since \Gamma(s,0)=\Gamma(s), it follows that: :\operatorname_j(x,0) = \operatorname_j(x) where \operatorname_j(x) is the complete Fermi-Dirac integral. Spe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
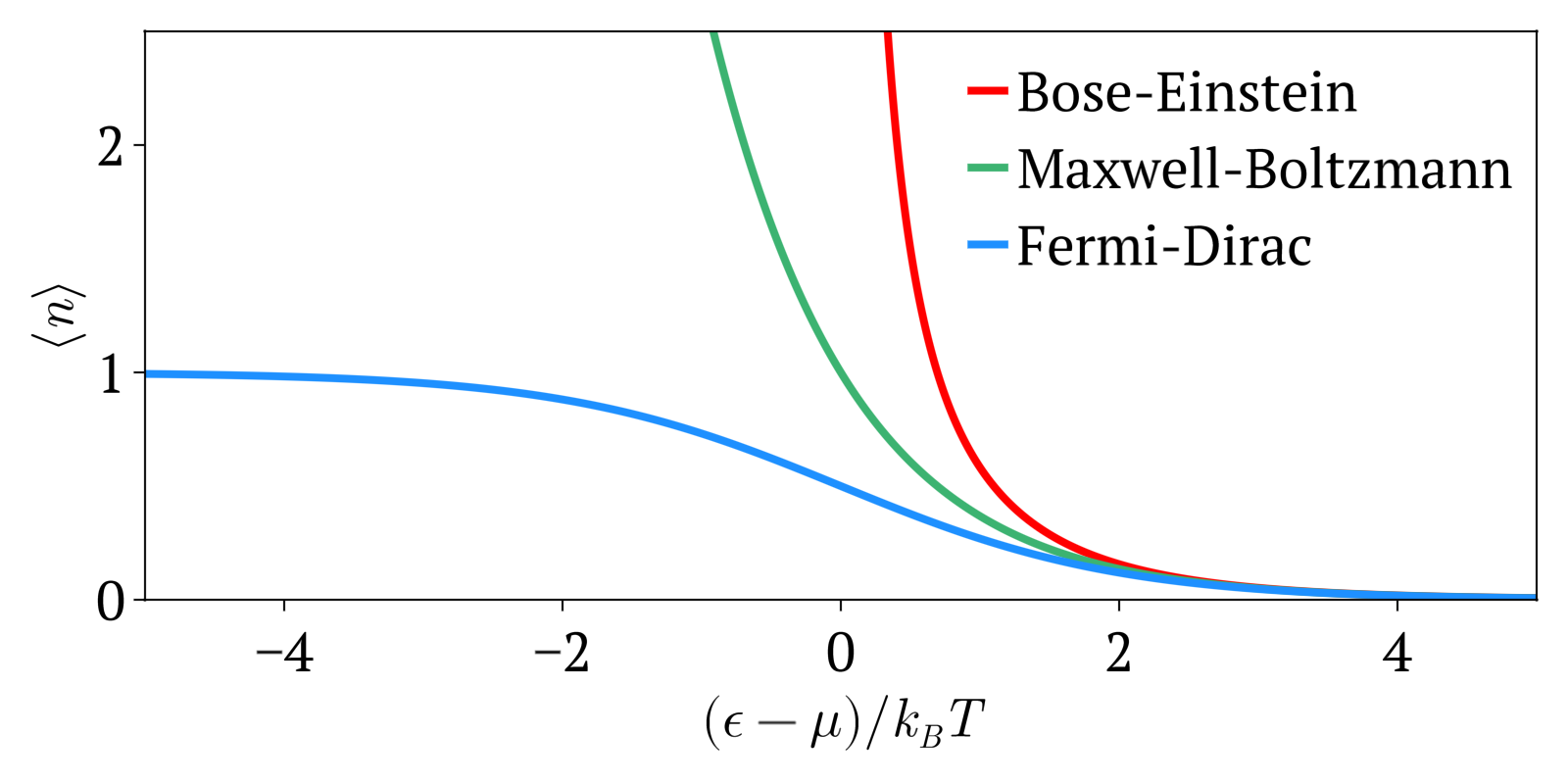
Bose–Einstein Statistics
In quantum statistics, Bose–Einstein statistics (B–E statistics) describes one of two possible ways in which a collection of non-interacting identical particles may occupy a set of available discrete energy states at thermodynamic equilibrium. The aggregation of particles in the same state, which is a characteristic of particles obeying Bose–Einstein statistics, accounts for the cohesive streaming of laser light and the frictionless creeping of superfluid helium. The theory of this behaviour was developed (1924–25) by Satyendra Nath Bose, who recognized that a collection of identical and indistinguishable particles could be distributed in this way. The idea was later adopted and extended by Albert Einstein in collaboration with Bose. Bose–Einstein statistics apply only to particles that do not follow the Pauli exclusion principle restrictions. Particles that follow Bose-Einstein statistics are called bosons, which have integer values of spin. In contrast, particles ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gamma Function
In mathematics, the gamma function (represented by Γ, capital Greek alphabet, Greek letter gamma) is the most common extension of the factorial function to complex numbers. Derived by Daniel Bernoulli, the gamma function \Gamma(z) is defined for all complex numbers z except non-positive integers, and for every positive integer z=n, \Gamma(n) = (n-1)!\,.The gamma function can be defined via a convergent improper integral for complex numbers with positive real part: \Gamma(z) = \int_0^\infty t^ e^\textt, \ \qquad \Re(z) > 0\,.The gamma function then is defined in the complex plane as the analytic continuation of this integral function: it is a meromorphic function which is holomorphic function, holomorphic except at zero and the negative integers, where it has simple Zeros and poles, poles. The gamma function has no zeros, so the reciprocal gamma function is an entire function. In fact, the gamma function corresponds to the Mellin transform of the negative exponential functi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Incomplete Gamma Function
In mathematics, the upper and lower incomplete gamma functions are types of special functions which arise as solutions to various mathematical problems such as certain integrals. Their respective names stem from their integral definitions, which are defined similarly to the gamma function but with different or "incomplete" integral limits. The gamma function is defined as an integral from zero to infinity. This contrasts with the lower incomplete gamma function, which is defined as an integral from zero to a variable upper limit. Similarly, the upper incomplete gamma function is defined as an integral from a variable lower limit to infinity. Definition The upper incomplete gamma function is defined as: \Gamma(s,x) = \int_x^ t^\,e^\, dt , whereas the lower incomplete gamma function is defined as: \gamma(s,x) = \int_0^x t^\,e^\, dt . In both cases is a complex parameter, such that the real part of is positive. Properties By integration by parts we find the recurrence relati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |