|
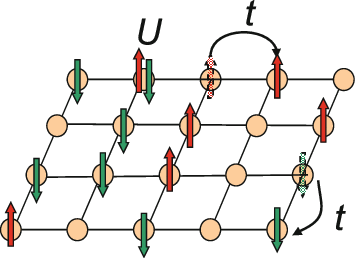
Hubbard Model
The Hubbard model is an Approximation, approximate model used to describe the transition between Conductor (material), conducting and Electrical insulation, insulating systems. It is particularly useful in solid-state physics. The model is named for John Hubbard (physicist), John Hubbard. The Hubbard model states that each electron experiences competing forces: one pushes it to tunnel to neighboring atoms, while the other pushes it away from its neighbors. Its Hamiltonian (quantum mechanics), Hamiltonian thus has two terms: a kinetic term allowing for Quantum tunneling, tunneling ("hopping") of particles between lattice sites and a potential term reflecting on-site interaction. The particles can either be fermions, as in Hubbard's original work, or bosons, in which case the model is referred to as the "Bose–Hubbard model". The Hubbard model is a useful approximation for particles in a periodic potential at sufficiently low temperatures, where all the particles may be assumed t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Martin Gutzwiller
Martin Charles Gutzwiller (12 October 1925 – 3 March 2014) was a Swiss-American physicist, known for his work on field theory, quantum chaos, and complex systems. He spent most of his career at IBM Research, and was also an adjunct professor of physics at Yale University. Biography Gutzwiller was born on October 12, 1925, in the Swiss city of Basel. He completed a Diploma degree from ETH Zurich, where he studied quantum physics under Wolfgang Pauli. He then went to the University of Kansas and completed a Ph.D under Max Dresden. After graduation, he worked on microwave engineering for Brown, Boveri & Cie, on geophysics for Shell Oil, and eventually for IBM Research in Switzerland, New York City, and Yorktown Heights, until his retirement in 1993. He also held temporary teaching appointments at Columbia University, ETH Zurich, Paris-Orsay, and Stockholm. He was Vice Chair for the Committee on Mathematical Physics, of the International Union of Pure and Applied Phy ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lattice Parameter
A lattice constant or lattice parameter is one of the physical dimensions and angles that determine the geometry of the unit cells in a crystal lattice, and is proportional to the distance between atoms in the crystal. A simple cubic crystal has only one lattice constant, the distance between atoms, but, in general, lattices in three dimensions have six lattice constants: the lengths ''a'', ''b'', and ''c'' of the three cell edges meeting at a vertex, and the angles ''α'', ''β'', and ''γ'' between those edges. The crystal lattice parameters ''a'', ''b'', and ''c'' have the dimension of length. The three numbers represent the size of the unit cell, that is, the distance from a given atom to an identical atom in the same position and orientation in a neighboring cell (except for very simple crystal structures, this will not necessarily be distance to the nearest neighbor). Their SI unit is the meter, and they are traditionally specified in angstroms (Å); an angstrom being 0.1 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Atomic Number
The atomic number or nuclear charge number (symbol ''Z'') of a chemical element is the charge number of its atomic nucleus. For ordinary nuclei composed of protons and neutrons, this is equal to the proton number (''n''p) or the number of protons found in the nucleus of every atom of that element. The atomic number can be used to uniquely identify ordinary chemical elements. In an ordinary uncharged atom, the atomic number is also equal to the number of electrons. For an ordinary atom which contains protons, neutrons and electrons, the sum of the atomic number ''Z'' and the neutron number ''N'' gives the atom's atomic mass number ''A''. Since protons and neutrons have approximately the same mass (and the mass of the electrons is negligible for many purposes) and the mass defect of the nucleon binding is always small compared to the nucleon mass, the atomic mass of any atom, when expressed in daltons (making a quantity called the " relative isotopic mass"), is within 1% ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pyrochlore
Pyrochlore () is a mineral group of the niobium end member of the pyrochlore supergroup. Pyrochlore is also a term for the crystal structure ''F''dm. The name is from the Greek , ''fire'', and , ''green'' because it typically turns green on ignition in classic blowpipe analysis. Mineral The general formula, (where A and B are metals), represent a family of phases isostructural to the mineral pyrochlore. Pyrochlores are an important class of materials in diverse technological applications such as luminescence, ionic conductivity, nuclear waste immobilization, high-temperature thermal barrier coatings, automobile exhaust gas control, catalysts, solid oxide fuel cell, ionic/electrical conductors etc. The mineral is associated with the metasomatic end stages of magmatic intrusions. Pyrochlore crystals are usually well-formed (euhedral), occurring usually as octahedra of a yellowish or brownish color and resinous luster. It is commonly metamict due to radiation damage from includ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rare-earth
The rare-earth elements (REE), also called the rare-earth metals or rare earths, and sometimes the lanthanides or lanthanoids (although scandium and yttrium, which do not belong to this series, are usually included as rare earths), are a set of 17 nearly indistinguishable lustrous silvery-white soft heavy metals. Compounds containing rare earths have diverse applications in electrical and electronic components, lasers, glass, magnetic materials, and industrial processes. The term "rare-earth" is a misnomer because they are not actually scarce, but historically it took a long time to isolate these elements. They are relatively plentiful in the entire Earth's crust (cerium being the 25th-most-abundant element at 68 parts per million, more abundant than copper), but in practice they are spread thinly as trace impurities, so to obtain rare earths at usable purity requires processing enormous amounts of raw ore at great expense; thus the name "rare" earths. Scandium and yttrium are ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Metal
A metal () is a material that, when polished or fractured, shows a lustrous appearance, and conducts electrical resistivity and conductivity, electricity and thermal conductivity, heat relatively well. These properties are all associated with having electrons available at the Fermi level, as against nonmetallic materials which do not. Metals are typically ductile (can be drawn into a wire) and malleable (can be shaped via hammering or pressing). A metal may be a chemical element such as iron; an alloy such as stainless steel; or a molecular compound such as polythiazyl, polymeric sulfur nitride. The general science of metals is called metallurgy, a subtopic of materials science; aspects of the electronic and thermal properties are also within the scope of condensed matter physics and solid-state chemistry, it is a multidisciplinary topic. In colloquial use materials such as steel alloys are referred to as metals, while others such as polymers, wood or ceramics are nonmetallic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kinetic Energy
In physics, the kinetic energy of an object is the form of energy that it possesses due to its motion. In classical mechanics, the kinetic energy of a non-rotating object of mass ''m'' traveling at a speed ''v'' is \fracmv^2.Resnick, Robert and Halliday, David (1960) ''Physics'', Section 7-5, Wiley International Edition The kinetic energy of an object is equal to the work, or force ( F) in the direction of motion times its displacement ( s), needed to accelerate the object from rest to its given speed. The same amount of work is done by the object when decelerating from its current speed to a state of rest. The SI unit of energy is the joule, while the English unit of energy is the foot-pound. In relativistic mechanics, \fracmv^2 is a good approximation of kinetic energy only when ''v'' is much less than the speed of light. History and etymology The adjective ''kinetic'' has its roots in the Greek word κίνησις ''kinesis'', meaning "motion". The dichoto ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Electric-field Screening
In physics, screening is the damping of electric fields caused by the presence of mobile charge carriers. It is an important part of the behavior of charge-carrying mediums, such as ionized gases (classical plasmas), electrolytes, and electronic conductors (semiconductors, metals). In a fluid, with a given permittivity , composed of electrically charged constituent particles, each pair of particles (with charges and ) interact through the Coulomb force as \mathbf = \frac\hat, where the vector is the relative position between the charges. This interaction complicates the theoretical treatment of the fluid. For example, a naive quantum mechanical calculation of the ground-state energy density yields infinity, which is unreasonable. The difficulty lies in the fact that even though the Coulomb force diminishes with distance as , the average number of particles at each distance is proportional to , assuming the fluid is fairly isotropic. As a result, a charge fluctuation at any on ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Electronic Band Structure
In solid-state physics, the electronic band structure (or simply band structure) of a solid describes the range of energy levels that electrons may have within it, as well as the ranges of energy that they may not have (called ''band gaps'' or ''forbidden bands''). Band theory derives these bands and band gaps by examining the allowed quantum mechanical wave functions for an electron in a large, periodic lattice of atoms or molecules. Band theory has been successfully used to explain many physical properties of solids, such as electrical resistivity and optical absorption, and forms the foundation of the understanding of all solid-state devices (transistors, solar cells, etc.). Why bands and band gaps occur The formation of electronic bands and band gaps can be illustrated with two complementary models for electrons in solids. The first one is the nearly free electron model, in which the electrons are assumed to move almost freely within the material. In this model, the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Crystal
A crystal or crystalline solid is a solid material whose constituents (such as atoms, molecules, or ions) are arranged in a highly ordered microscopic structure, forming a crystal lattice that extends in all directions. In addition, macroscopic single crystals are usually identifiable by their geometrical shape, consisting of flat faces with specific, characteristic orientations. The scientific study of crystals and crystal formation is known as crystallography. The process of crystal formation via mechanisms of crystal growth is called crystallization or solidification. The word ''crystal'' derives from the Ancient Greek word (), meaning both "ice" and " rock crystal", from (), "icy cold, frost". Examples of large crystals include snowflakes, diamonds, and table salt. Most inorganic solids are not crystals but polycrystals, i.e. many microscopic crystals fused together into a single solid. Polycrystals include most metals, rocks, ceramics, and ice. A third cat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eigenstates
In quantum physics, a quantum state is a mathematical entity that embodies the knowledge of a quantum system. Quantum mechanics specifies the construction, evolution, and measurement of a quantum state. The result is a prediction for the system represented by the state. Knowledge of the quantum state, and the rules for the system's evolution in time, exhausts all that can be known about a quantum system. Quantum states may be defined differently for different kinds of systems or problems. Two broad categories are * wave functions describing quantum systems using position or momentum variables and * the more abstract vector quantum states. Historical, educational, and application-focused problems typically feature wave functions; modern professional physics uses the abstract vector states. In both categories, quantum states divide into pure versus mixed states, or into coherent states and incoherent states. Categories with special properties include stationary states for time i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |