|
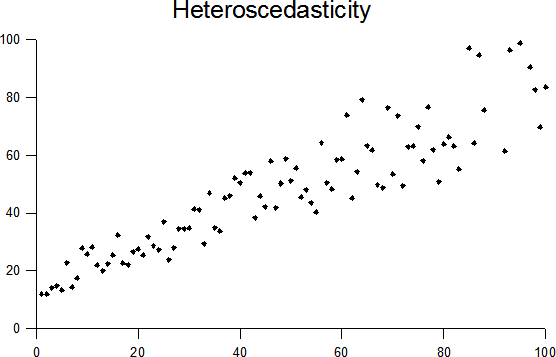
Heteroskedasticity
In statistics, a sequence (or a vector) of random variables is homoscedastic () if all its random variables have the same finite variance. This is also known as homogeneity of variance. The complementary notion is called heteroscedasticity. The spellings ''homoskedasticity'' and ''heteroskedasticity'' are also frequently used. Assuming a variable is homoscedastic when in reality it is heteroscedastic () results in unbiased but inefficient point estimates and in biased estimates of standard errors, and may result in overestimating the goodness of fit as measured by the Pearson coefficient. The existence of heteroscedasticity is a major concern in regression analysis and the analysis of variance, as it invalidates statistical tests of significance that assume that the modelling errors all have the same variance. While the ordinary least squares estimator is still unbiased in the presence of heteroscedasticity, it is inefficient and generalized least squares should be used ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Autoregressive Conditional Heteroscedasticity
In econometrics, the autoregressive conditional heteroskedasticity (ARCH) model is a statistical model for time series data that describes the variance of the current error term or innovation as a function of the actual sizes of the previous time periods' error terms; often the variance is related to the squares of the previous innovations. The ARCH model is appropriate when the error variance in a time series follows an autoregressive (AR) model; if an autoregressive moving average (ARMA) model is assumed for the error variance, the model is a generalized autoregressive conditional heteroskedasticity (GARCH) model. ARCH models are commonly employed in modeling financial time series that exhibit time-varying volatility and volatility clustering, i.e. periods of swings interspersed with periods of relative calm. ARCH-type models are sometimes considered to be in the family of stochastic volatility models, although this is strictly incorrect since at time ''t'' the volatility i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Econometrica
''Econometrica'' is a peer-reviewed academic journal of economics, publishing articles in many areas of economics, especially econometrics. It is published by Wiley-Blackwell on behalf of the Econometric Society. The current editor-in-chief An editor-in-chief (EIC), also known as lead editor or chief editor, is a publication's editorial leader who has final responsibility for its operations and policies. The highest-ranking editor of a publication may also be titled editor, managing ... is Guido Imbens. History ''Econometrica'' was established in 1933. Its first editor was Ragnar Frisch, recipient of the first Nobel Memorial Prize in Economic Sciences in 1969, who served as an editor from 1933 to 1954. Although ''Econometrica'' is currently published entirely in English, the first few issues also contained scientific articles written in French. Indexing and abstracting ''Econometrica'' is abstracted and indexed in: * Scopus * EconLit * Social Science Citation Inde ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
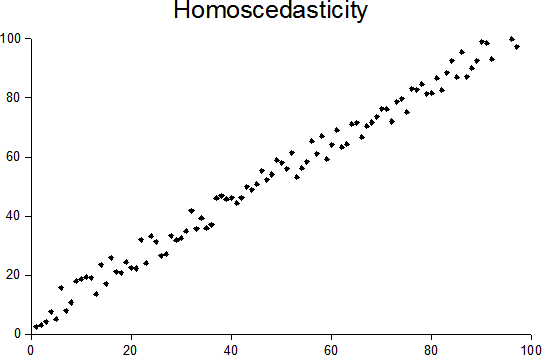
Homoscedasticity
In statistics, a sequence (or a vector) of random variables is homoscedastic () if all its random variables have the same finite variance. This is also known as homogeneity of variance. The complementary notion is called heteroscedasticity. The spellings ''homoskedasticity'' and ''heteroskedasticity'' are also frequently used. Assuming a variable is homoscedastic when in reality it is heteroscedastic () results in unbiased but inefficient point estimates and in biased estimates of standard errors, and may result in overestimating the goodness of fit as measured by the Pearson coefficient. The existence of heteroscedasticity is a major concern in regression analysis and the analysis of variance, as it invalidates statistical tests of significance that assume that the modelling errors all have the same variance. While the ordinary least squares estimator is still unbiased in the presence of heteroscedasticity, it is inefficient and generalized least squares should be used i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Robert Engle
Robert Fry Engle III (born November 10, 1942) is an American economist and statistician. He won the 2003 Nobel Memorial Prize in Economic Sciences, sharing the award with Clive Granger, "for methods of analyzing economic time series with time-varying volatility (ARCH)". Biography Engle was born in Syracuse, New York into Quaker family and went on to graduate from Williams College with a BS in physics. He earned an MS in physics and a PhD in economics, both from Cornell University in 1966 and 1969 respectively. After completing his PhD, Engle became an economics professor at the Massachusetts Institute of Technology from 1969 to 1977. He joined the faculty of the University of California, San Diego (UCSD) in 1975, wherefrom he retired in 2003. He now holds positions of Professor Emeritus and Research Professor at UCSD. He currently teaches at New York University, Stern School of Business where he is the Michael Armellino professor in Management of Financial Services. At New Yor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Generalized Least Squares
In statistics, generalized least squares (GLS) is a technique for estimating the unknown parameters in a linear regression model when there is a certain degree of correlation between the residuals in a regression model. In these cases, ordinary least squares and weighted least squares can be statistically inefficient, or even give misleading inferences. GLS was first described by Alexander Aitken in 1936. Method outline In standard linear regression models we observe data \_ on ''n'' statistical units. The response values are placed in a vector \mathbf = \left( y_, \dots, y_ \right)^, and the predictor values are placed in the design matrix \mathbf = \left( \mathbf_^, \dots, \mathbf_^ \right)^, where \mathbf_ = \left( 1, x_, \dots, x_ \right) is a vector of the ''k'' predictor variables (including a constant) for the ''i''th unit. The model forces the conditional mean of \mathbf given \mathbf to be a linear function of \mathbf, and assumes the conditional variance of th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gauss–Markov Theorem
In statistics, the Gauss–Markov theorem (or simply Gauss theorem for some authors) states that the ordinary least squares (OLS) estimator has the lowest sampling variance within the class of linear unbiased estimators, if the errors in the linear regression model are uncorrelated, have equal variances and expectation value of zero. The errors do not need to be normal, nor do they need to be independent and identically distributed (only uncorrelated with mean zero and homoscedastic with finite variance). The requirement that the estimator be unbiased cannot be dropped, since biased estimators exist with lower variance. See, for example, the James–Stein estimator (which also drops linearity), ridge regression, or simply any degenerate estimator. The theorem was named after Carl Friedrich Gauss and Andrey Markov, although Gauss' work significantly predates Markov's. But while Gauss derived the result under the assumption of independence and normality, Markov reduced ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Heteroscedasticity
In statistics, a sequence (or a vector) of random variables is homoscedastic () if all its random variables have the same finite variance. This is also known as homogeneity of variance. The complementary notion is called heteroscedasticity. The spellings ''homoskedasticity'' and ''heteroskedasticity'' are also frequently used. Assuming a variable is homoscedastic when in reality it is heteroscedastic () results in unbiased but inefficient point estimates and in biased estimates of standard errors, and may result in overestimating the goodness of fit as measured by the Pearson coefficient. The existence of heteroscedasticity is a major concern in regression analysis and the analysis of variance, as it invalidates statistical tests of significance that assume that the modelling errors all have the same variance. While the ordinary least squares estimator is still unbiased in the presence of heteroscedasticity, it is inefficient and generalized least squares should be used i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Normal Distribution
In statistics, a normal distribution or Gaussian distribution is a type of continuous probability distribution for a real-valued random variable. The general form of its probability density function is : f(x) = \frac e^ The parameter \mu is the mean or expectation of the distribution (and also its median and mode), while the parameter \sigma is its standard deviation. The variance of the distribution is \sigma^2. A random variable with a Gaussian distribution is said to be normally distributed, and is called a normal deviate. Normal distributions are important in statistics and are often used in the natural and social sciences to represent real-valued random variables whose distributions are not known. Their importance is partly due to the central limit theorem. It states that, under some conditions, the average of many samples (observations) of a random variable with finite mean and variance is itself a random variable—whose distribution converges to a normal dist ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Best Linear Unbiased Estimator
Best or The Best may refer to: People * Best (surname), people with the surname Best * Best (footballer, born 1968), retired Portuguese footballer Companies and organizations * Best & Co., an 1879–1971 clothing chain * Best Lock Corporation, a lock manufacturer * Best Manufacturing Company, a farm machinery company * Best Products, a chain of catalog showroom retail stores * Brihanmumbai Electric Supply and Transport, a public transport and utility provider * Best High School (other) Acronyms * Berkeley Earth Surface Temperature, a project to assess global temperature records * BEST Robotics, a student competition * BioEthanol for Sustainable Transport * Bootstrap error-adjusted single-sample technique, a statistical method * Bringing Examination and Search Together, a European Patent Office initiative * Bronx Environmental Stewardship Training, a program of the Sustainable South Bronx organization * Smart BEST, a Japanese experimental train * Brihanmumbai Electr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Econometrician
Econometrics is the application of statistical methods to economic data in order to give empirical content to economic relationships. M. Hashem Pesaran (1987). "Econometrics," '' The New Palgrave: A Dictionary of Economics'', v. 2, p. 8 p. 8–22 Reprinted in J. Eatwell ''et al.'', eds. (1990). ''Econometrics: The New Palgrave''p. 1 p. 1–34Abstract (2008 revision by J. Geweke, J. Horowitz, and H. P. Pesaran). More precisely, it is "the quantitative analysis of actual economic phenomena based on the concurrent development of theory and observation, related by appropriate methods of inference". An introductory economics textbook describes econometrics as allowing economists "to sift through mountains of data to extract simple relationships". Jan Tinbergen is one of the two founding fathers of econometrics. The other, Ragnar Frisch, also coined the term in the sense in which it is used today. A basic tool for econometrics is the multiple linear regression model. ''Econometric th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
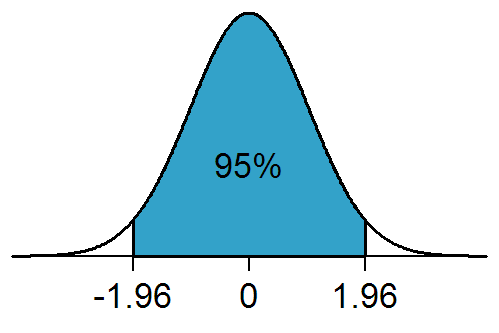
Statistical Significance
In statistical hypothesis testing, a result has statistical significance when it is very unlikely to have occurred given the null hypothesis (simply by chance alone). More precisely, a study's defined significance level, denoted by \alpha, is the probability of the study rejecting the null hypothesis, given that the null hypothesis is true; and the ''p''-value of a result, ''p'', is the probability of obtaining a result at least as extreme, given that the null hypothesis is true. The result is statistically significant, by the standards of the study, when p \le \alpha. The significance level for a study is chosen before data collection, and is typically set to 5% or much lower—depending on the field of study. In any experiment or observation that involves drawing a sample from a population, there is always the possibility that an observed effect would have occurred due to sampling error alone. But if the ''p''-value of an observed effect is less than (or equal to) the significan ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
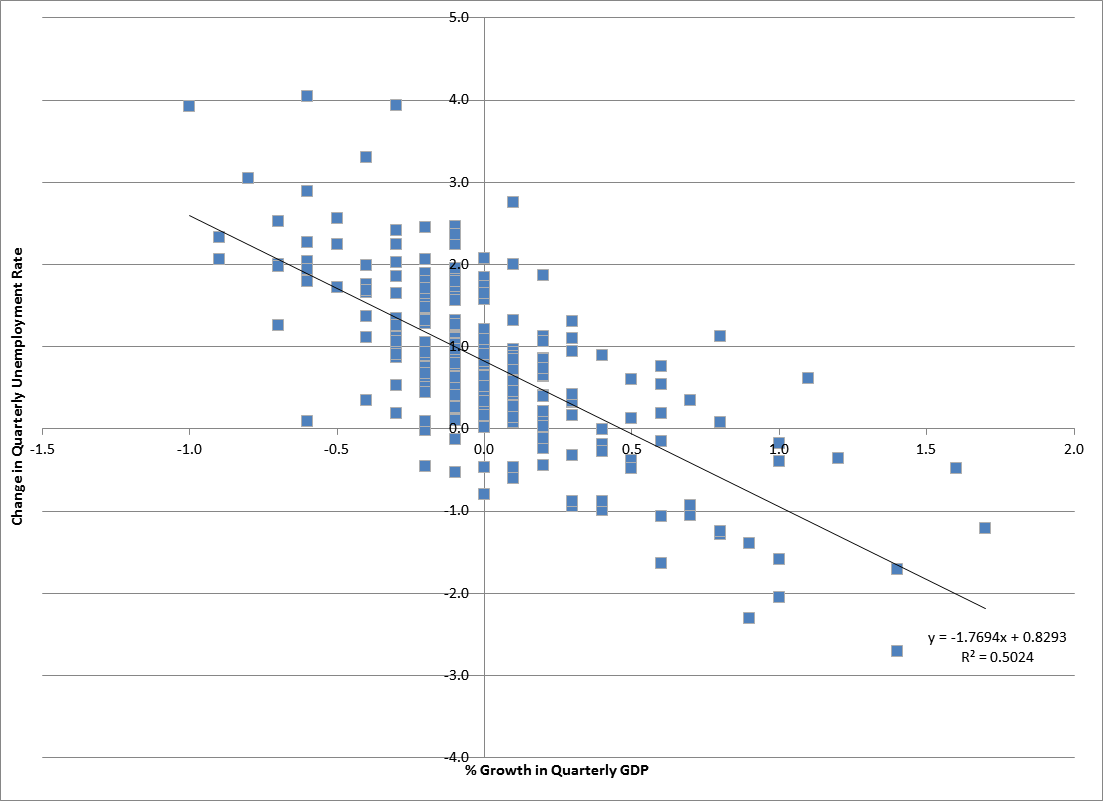
Scedastic Function
In probability theory and statistics, a conditional variance is the variance of a random variable given the value(s) of one or more other variables. Particularly in econometrics, the conditional variance is also known as the scedastic function or skedastic function. Conditional variances are important parts of autoregressive conditional heteroskedasticity (ARCH) models. Definition The conditional variance of a random variable ''Y'' given another random variable ''X'' is :\operatorname(Y, X) = \operatorname\Big(\big(Y - \operatorname(Y\mid X)\big)^\mid X\Big). The conditional variance tells us how much variance is left if we use \operatorname(Y\mid X) to "predict" ''Y''. Here, as usual, \operatorname(Y\mid X) stands for the conditional expectation of ''Y'' given ''X'', which we may recall, is a random variable itself (a function of ''X'', determined up to probability one). As a result, \operatorname(Y, X) itself is a random variable (and is a function of ''X''). Explanation, rel ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |