|
Hamming Weight
The Hamming weight of a string (computer science), string is the number of symbols that are different from the zero-symbol of the alphabet used. It is thus equivalent to the Hamming distance from the all-zero string of the same length. For the most typical case, a given set of bits, this is the number of bits set to 1, or the digit sum of the Binary numeral system, binary representation of a given number and the Taxicab geometry, ''ℓ''₁ norm of a bit vector. In this binary case, it is also called the population count, popcount, sideways sum, or bit summation. History and usage The Hamming weight is named after the American mathematician Richard Hamming, although he did not originate the notion. The Hamming weight of binary numbers was already used in 1899 by James Whitbread Lee Glaisher, James W. L. Glaisher to give a formula for Gould's sequence, the number of odd binomial coefficients in a single row of Pascal's triangle. Irving S. Reed introduced a concept, equivalen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
String (computer Science)
In computer programming, a string is traditionally a sequence of character (computing), characters, either as a literal (computer programming), literal constant or as some kind of Variable (computer science), variable. The latter may allow its elements to be Immutable object, mutated and the length changed, or it may be fixed (after creation). A string is often implemented as an array data structure of bytes (or word (computer architecture), words) that stores a sequence of elements, typically characters, using some character encoding. More general, ''string'' may also denote a sequence (or List (abstract data type), list) of data other than just characters. Depending on the programming language and precise data type used, a variable (programming), variable declared to be a string may either cause storage in memory to be statically allocated for a predetermined maximum length or employ dynamic allocation to allow it to hold a variable number of elements. When a string appears lit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chord (distributed Hash Table)
In computing, Chord is a protocol and algorithm for a peer-to-peer distributed hash table. A distributed hash table stores key-value pairs by assigning keys to different computers (known as "nodes"); a node will store the values for all the keys for which it is responsible. Chord specifies how keys are assigned to nodes, and how a node can discover the value for a given key by first locating the node responsible for that key. Chord is one of the four original distributed hash table protocols, along with CAN, Tapestry, and Pastry. It was introduced in 2001 by Ion Stoica, Robert Morris, David Karger, Frans Kaashoek, and Hari Balakrishnan, and was developed at MIT. The 2001 Chord paper won an ACM SIGCOMM Test of Time award in 2011. Subsequent research by Pamela Zave has shown that the original Chord algorithm (as specified in the 2001 SIGCOMM paper, the 2001 Technical report, the 2002 PODC paper, and the 2003 TON paper ) can mis-order the ring, produce several rings, and b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Block Code
In coding theory, block codes are a large and important family of error-correcting codes that encode data in blocks. There is a vast number of examples for block codes, many of which have a wide range of practical applications. The abstract definition of block codes is conceptually useful because it allows coding theorists, mathematicians, and computer scientists to study the limitations of ''all'' block codes in a unified way. Such limitations often take the form of ''bounds'' that relate different parameters of the block code to each other, such as its rate and its ability to detect and correct errors. Examples of block codes are Reed–Solomon codes, Hamming codes, Hadamard codes, Expander codes, Golay codes, Reed–Muller codes and Polar codes. These examples also belong to the class of linear codes, and hence they are called linear block codes. More particularly, these codes are known as algebraic block codes, or cyclic block codes, because they can be generated using ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Error-correcting Code
In computing, telecommunication, information theory, and coding theory, forward error correction (FEC) or channel coding is a technique used for controlling errors in data transmission over unreliable or noisy communication channels. The central idea is that the sender encodes the message in a redundant way, most often by using an error correction code, or error correcting code (ECC). The redundancy allows the receiver not only to detect errors that may occur anywhere in the message, but often to correct a limited number of errors. Therefore a reverse channel to request re-transmission may not be needed. The cost is a fixed, higher forward channel bandwidth. The American mathematician Richard Hamming pioneered this field in the 1940s and invented the first error-correcting code in 1950: the Hamming (7,4) code. FEC can be applied in situations where re-transmissions are costly or impossible, such as one-way communication links or when transmitting to multiple receivers in m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bitwise AND
In computer programming, a bitwise operation operates on a bit string, a bit array or a binary numeral (considered as a bit string) at the level of its individual bits. It is a fast and simple action, basic to the higher-level arithmetic operations and directly supported by the processor. Most bitwise operations are presented as two-operand instructions where the result replaces one of the input operands. On simple low-cost processors, typically, bitwise operations are substantially faster than division, several times faster than multiplication, and sometimes significantly faster than addition. While modern processors usually perform addition and multiplication just as fast as bitwise operations due to their longer instruction pipelines and other architectural design choices, bitwise operations do commonly use less power because of the reduced use of resources. Bitwise operators In the explanations below, any indication of a bit's position is counted from the right (least sig ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
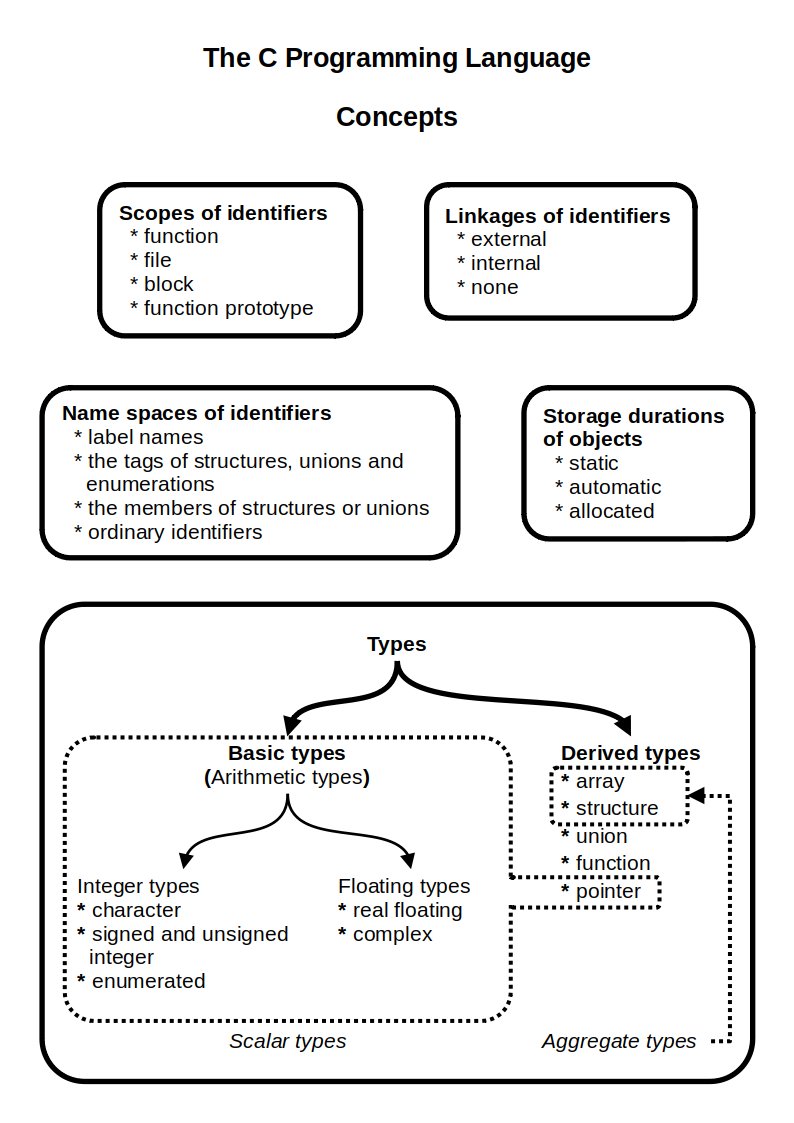
C (programming Language)
C (''pronounced'' '' – like the letter c'') is a general-purpose programming language. It was created in the 1970s by Dennis Ritchie and remains very widely used and influential. By design, C's features cleanly reflect the capabilities of the targeted Central processing unit, CPUs. It has found lasting use in operating systems code (especially in Kernel (operating system), kernels), device drivers, and protocol stacks, but its use in application software has been decreasing. C is commonly used on computer architectures that range from the largest supercomputers to the smallest microcontrollers and embedded systems. A successor to the programming language B (programming language), B, C was originally developed at Bell Labs by Ritchie between 1972 and 1973 to construct utilities running on Unix. It was applied to re-implementing the kernel of the Unix operating system. During the 1980s, C gradually gained popularity. It has become one of the most widely used programming langu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Processor Support
Processor may refer to: Computing Hardware * Processor (computing) ** Central processing unit (CPU), the hardware within a computer that executes a program *** Microprocessor, a central processing unit contained on a single integrated circuit (IC) **** Application-specific instruction set processor (ASIP), a component used in system-on-a-chip design **** Graphics processing unit (GPU), a processor designed for doing dedicated graphics-rendering computations **** Physics processing unit (PPU), a dedicated microprocessor designed to handle the calculations of physics **** Digital signal processor (DSP), a specialized microprocessor designed specifically for digital signal processing ***** Image processor, a specialized DSP used for image processing in digital cameras, mobile phones or other devices **** Neural processing unit (NPU), a class of specialized hardware accelerator or computer system designed to accelerate artificial intelligence and machine learning applications, inc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bit Array
A bit array (also known as bitmask, bit map, bit set, bit string, or bit vector) is an array data structure that compactly stores bits. It can be used to implement a simple set data structure. A bit array is effective at exploiting bit-level parallelism in hardware to perform operations quickly. A typical bit array stores ''kw'' bits, where ''w'' is the number of bits in the unit of storage, such as a byte or Word (computer architecture), word, and ''k'' is some nonnegative integer. If ''w'' does not divide the number of bits to be stored, some space is wasted due to Fragmentation (computing), internal fragmentation. Definition A bit array is a mapping from some domain (almost always a range of integers) to values in the set . The values can be interpreted as dark/light, absent/present, locked/unlocked, valid/invalid, et cetera. The point is that there are only two possible values, so they can be stored in one bit. As with other arrays, the access to a single bit can be managed ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Binary Number
A binary number is a number expressed in the Radix, base-2 numeral system or binary numeral system, a method for representing numbers that uses only two symbols for the natural numbers: typically "0" (zero) and "1" (one). A ''binary number'' may also refer to a rational number that has a finite representation in the binary numeral system, that is, the quotient of an integer by a power of two. The base-2 numeral system is a positional notation with a radix of 2. Each digit is referred to as a bit, or binary digit. Because of its straightforward implementation in digital electronic circuitry using logic gates, the binary system is used by almost all modern computer, computers and computer-based devices, as a preferred system of use, over various other human techniques of communication, because of the simplicity of the language and the noise immunity in physical implementation. History The modern binary number system was studied in Europe in the 16th and 17th centuries by Thoma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Unary Numeral System
The unary numeral system is the simplest numeral system to represent natural numbers: to represent a number ''N'', a symbol representing 1 is repeated ''N'' times. In the unary system, the number 0 (zero) is represented by the empty string, that is, the absence of a symbol. Numbers 1, 2, 3, 4, 5, 6, ... are represented in unary as 1, 11, 111, 1111, 11111, 111111, ... Unary is a bijective numeral system. However, although it has sometimes been described as "base 1", it differs in some important ways from positional notations, in which the value of a digit depends on its position within a number. For instance, the unary form of a number can be exponentially longer than its representation in other bases. The use of tally marks in counting is an application of the unary numeral system. For example, using the tally mark (𝍷), the number 3 is represented as . In East Asian cultures, the number 3 is represented as 三, a character drawn with three strokes. (One and two are repres ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Find First Set
In computer software and hardware, find first set (ffs) or find first one is a bit operation that, given an unsigned Word (computer architecture), machine word, designates the index or position of the least significant bit set to one in the word counting from the least significant bit position. A nearly equivalent operation is count trailing zeros (ctz) or number of trailing zeros (ntz), which counts the number of zero bits following the least significant one bit. The complementary operation that finds the index or position of the most significant set bit is log base 2, so called because it computes the binary logarithm . This is #Properties and relations, closely related to count leading zeros (clz) or number of leading zeros (nlz), which counts the number of zero bits preceding the most significant one bit. There are two common variants of find first set, the POSIX definition which starts indexing of bits at 1, herein labelled ffs, and the variant which starts indexing of bits at ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |