|
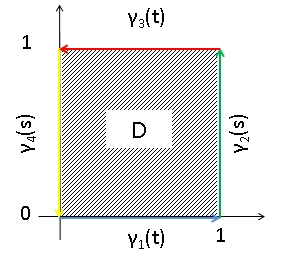
Green's Theorem
In vector calculus, Green's theorem relates a line integral around a simple closed curve to a double integral over the plane region bounded by . It is the two-dimensional special case of Stokes' theorem. Theorem Let be a positively oriented, piecewise smooth, simple closed curve in a plane, and let be the region bounded by . If and are functions of defined on an open region containing and have continuous partial derivatives there, then \oint_C (L\, dx + M\, dy) = \iint_ \left(\frac - \frac\right) dx\, dy where the path of integration along is anticlockwise. In physics, Green's theorem finds many applications. One is solving two-dimensional flow integrals, stating that the sum of fluid outflowing from a volume is equal to the total outflow summed about an enclosing area. In plane geometry, and in particular, area surveying, Green's theorem can be used to determine the area and centroid of plane figures solely by integrating over the perimeter. Proof when ''D ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Method Of Image Charges
The method of image charges (also known as the method of images and method of mirror charges) is a basic problem-solving tool in electrostatics. The name originates from the replacement of certain elements in the original layout with imaginary charges, which replicates the boundary conditions of the problem (see Dirichlet boundary conditions or Neumann boundary conditions). The validity of the method of image charges rests upon a corollary of the uniqueness theorem, which states that the electric potential in a volume ''V'' is uniquely determined if both the charge density throughout the region and the value of the electric potential on all boundaries are specified. Alternatively, application of this corollary to the differential form of Gauss' Law shows that in a volume ''V'' surrounded by conductors and containing a specified charge density ''ρ'', the electric field is uniquely determined if the total charge on each conductor is given. Possessing knowledge of either the el ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bernhard Riemann
Georg Friedrich Bernhard Riemann (; 17 September 1826 – 20 July 1866) was a German mathematician who made contributions to analysis, number theory, and differential geometry. In the field of real analysis, he is mostly known for the first rigorous formulation of the integral, the Riemann integral, and his work on Fourier series. His contributions to complex analysis include most notably the introduction of Riemann surfaces, breaking new ground in a natural, geometric treatment of complex analysis. His 1859 paper on the prime-counting function, containing the original statement of the Riemann hypothesis, is regarded as a foundational paper of analytic number theory. Through his pioneering contributions to differential geometry, Riemann laid the foundations of the mathematics of general relativity. He is considered by many to be one of the greatest mathematicians of all time. Biography Early years Riemann was born on 17 September 1826 in Breselenz, a village near ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Augustin-Louis Cauchy
Baron Augustin-Louis Cauchy (, ; ; 21 August 178923 May 1857) was a French mathematician, engineer, and physicist who made pioneering contributions to several branches of mathematics, including mathematical analysis and continuum mechanics. He was one of the first to state and rigorously prove theorems of calculus, rejecting the heuristic principle of the generality of algebra of earlier authors. He almost singlehandedly founded complex analysis and the study of permutation groups in abstract algebra. A profound mathematician, Cauchy had a great influence over his contemporaries and successors; Hans Freudenthal stated: "More concepts and theorems have been named for Cauchy than for any other mathematician (in elasticity alone there are sixteen concepts and theorems named for Cauchy)." Cauchy was a prolific writer; he wrote approximately eight hundred research articles and five complete textbooks on a variety of topics in the fields of mathematics and mathematical physics. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
An Essay On The Application Of Mathematical Analysis To The Theories Of Electricity And Magnetism
''An Essay on the Application of Mathematical Analysis to the Theories of Electricity and Magnetism'' is a fundamental publication by George Green in 1828, where he extends previous work of Siméon Denis Poisson on electricity and magnetism. The work in mathematical analysis, notably including what is now universally known as Green's theorem, is of the greatest importance in all branches of mathematical physics. It contains the first exposition of the theory of potential. In physics, Green's theorem is mostly used to solve two-dimensional flow integrals, stating that the sum of fluid outflows at any point inside a volume is equal to the total outflow summed about an enclosing area. In plane geometry, and in particular, area surveying, Green's theorem can be used to determine the area and centroid of plane figures solely by integrating over the perimeter. It is in this essay that the term ' potential function' first occurs. Herein also his remarkable theorem in pure math ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
George Green (mathematician)
George Green (14 July 1793 – 31 May 1841) was a British mathematical physicist who wrote ''An Essay on the Application of Mathematical Analysis to the Theories of Electricity and Magnetism'' in 1828. The essay introduced several important concepts, among them a theorem similar to the modern Green's theorem, the idea of potential functions as currently used in physics, and the concept of what are now called Green's functions. Green was the first person to create a mathematical theory of electricity and magnetism and his theory formed the foundation for the work of other scientists such as James Clerk Maxwell, William Thomson, and others. His work on potential theory ran parallel to that of Carl Friedrich Gauss. Green's life story is remarkable in that he was almost entirely self-taught. He received only about one year of formal schooling as a child, between the ages of 8 and 9. Early life Green was born and lived for most of his life in the English town of Sneinton, No ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Divergence Theorem
In vector calculus, the divergence theorem, also known as Gauss's theorem or Ostrogradsky's theorem, reprinted in is a theorem which relates the '' flux'' of a vector field through a closed surface to the ''divergence'' of the field in the volume enclosed. More precisely, the divergence theorem states that the surface integral of a vector field over a closed surface, which is called the "flux" through the surface, is equal to the volume integral of the divergence over the region inside the surface. Intuitively, it states that "the sum of all sources of the field in a region (with sinks regarded as negative sources) gives the net flux out of the region". The divergence theorem is an important result for the mathematics of physics and engineering, particularly in electrostatics and fluid dynamics. In these fields, it is usually applied in three dimensions. However, it generalizes to any number of dimensions. In one dimension, it is equivalent to integration by parts. In t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Exterior Derivative
On a differentiable manifold, the exterior derivative extends the concept of the differential of a function to differential forms of higher degree. The exterior derivative was first described in its current form by Élie Cartan in 1899. The resulting calculus, known as exterior calculus, allows for a natural, metric-independent generalization of Stokes' theorem, Gauss's theorem, and Green's theorem from vector calculus. If a differential -form is thought of as measuring the flux through an infinitesimal - parallelotope at each point of the manifold, then its exterior derivative can be thought of as measuring the net flux through the boundary of a -parallelotope at each point. Definition The exterior derivative of a differential form of degree (also differential -form, or just -form for brevity here) is a differential form of degree . If is a smooth function (a -form), then the exterior derivative of is the differential of . That is, is the unique -form such that f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Differential Form
In mathematics, differential forms provide a unified approach to define integrands over curves, surfaces, solids, and higher-dimensional manifolds. The modern notion of differential forms was pioneered by Élie Cartan. It has many applications, especially in geometry, topology and physics. For instance, the expression is an example of a -form, and can be integrated over an interval contained in the domain of : :\int_a^b f(x)\,dx. Similarly, the expression is a -form that can be integrated over a surface : :\int_S (f(x,y,z)\,dx\wedge dy + g(x,y,z)\,dz\wedge dx + h(x,y,z)\,dy\wedge dz). The symbol denotes the exterior product, sometimes called the ''wedge product'', of two differential forms. Likewise, a -form represents a volume element that can be integrated over a region of space. In general, a -form is an object that may be integrated over a -dimensional manifold, and is homogeneous of degree in the coordinate differentials dx, dy, \ldots. On an -dimensional mani ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euclidean Vector
In mathematics, physics, and engineering, a Euclidean vector or simply a vector (sometimes called a geometric vector or spatial vector) is a geometric object that has magnitude (or length) and direction. Vectors can be added to other vectors according to vector algebra. A Euclidean vector is frequently represented by a '' directed line segment'', or graphically as an arrow connecting an ''initial point'' ''A'' with a ''terminal point'' ''B'', and denoted by \overrightarrow . A vector is what is needed to "carry" the point ''A'' to the point ''B''; the Latin word ''vector'' means "carrier". It was first used by 18th century astronomers investigating planetary revolution around the Sun. The magnitude of the vector is the distance between the two points, and the direction refers to the direction of displacement from ''A'' to ''B''. Many algebraic operations on real numbers such as addition, subtraction, multiplication, and negation have close analogues for vectors, operati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stokes' Theorem
Stokes's theorem, also known as the Kelvin–Stokes theorem Nagayoshi Iwahori, et al.:"Bi-Bun-Seki-Bun-Gaku" Sho-Ka-Bou(jp) 1983/12Written in Japanese)Atsuo Fujimoto;"Vector-Kai-Seki Gendai su-gaku rekucha zu. C(1)" :ja:培風館, Bai-Fu-Kan(jp)(1979/01) [] (Written in Japanese) after Lord Kelvin and Sir George Stokes, 1st Baronet, George Stokes, the fundamental theorem for curls or simply the curl theorem, is a theorem in vector calculus on . Given a vector field, the theorem relates the integral of the curl of the vector field over some surface, to the line integral of the vector field around the boundary of the surface. The classical Stokes' theorem can be stated in one sentence: The line integral of a vector field over a loop is equal to the '' flux of its curl'' through the enclosed surface. Stokes' theorem is a special case of the generalized Stokes' theorem. In particular, a vector field on can be considered as a 1-form in which case its curl is its exterior deriv ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |