|
Gibbs' Inequality
200px, Josiah Willard Gibbs In information theory, Gibbs' inequality is a statement about the information entropy of a discrete probability distribution. Several other bounds on the entropy of probability distributions are derived from Gibbs' inequality, including Fano's inequality. It was first presented by J. Willard Gibbs in the 19th century. Gibbs' inequality Suppose that : P = \ is a discrete probability distribution. Then for any other probability distribution : Q = \ the following inequality between positive quantities (since pi and qi are between zero and one) holds: : - \sum_^n p_i \log p_i \leq - \sum_^n p_i \log q_i with equality if and only if : p_i = q_i for all ''i''. Put in words, the information entropy of a distribution P is less than or equal to its cross entropy with any other distribution Q. The difference between the two quantities is the Kullback–Leibler divergence or relative entropy, so the inequality can also be written: : D_(P\, Q) \equiv \ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Josiah Willard Gibbs -from MMS-
Josiah ( or ) or Yoshiyahu; la, Iosias was the 16th king of Judah (–609 BCE) who, according to the Hebrew Bible, instituted major religious reforms by removing official worship of gods other than Yahweh. Josiah is credited by most biblical scholars with having established or compiled important Hebrew scriptures during the "Deuteronomic reform" which probably occurred during his rule. Josiah became king of the Kingdom of Judah at the age of eight, after the assassination of his father, King Amon. Josiah reigned for 31 years, from 641/640 to 610/609 BCE. Josiah is known only from biblical texts; no reference to him exists in other surviving texts of the period from Egypt or Babylon, and no clear archaeological evidence, such as inscriptions bearing his name, has ever been found. Nevertheless, most scholars believe that he existed historically and that the absence of documents is due to few documents of any sort surviving from this period, and to Jerusalem having been occupied, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jensen's Inequality
In mathematics, Jensen's inequality, named after the Danish mathematician Johan Jensen, relates the value of a convex function of an integral to the integral of the convex function. It was proved by Jensen in 1906, building on an earlier proof of the same inequality for doubly-differentiable functions by Otto Hölder in 1889. Given its generality, the inequality appears in many forms depending on the context, some of which are presented below. In its simplest form the inequality states that the convex transformation of a mean is less than or equal to the mean applied after convex transformation; it is a simple corollary that the opposite is true of concave transformations. Jensen's inequality generalizes the statement that the secant line of a convex function lies ''above'' the graph of the function, which is Jensen's inequality for two points: the secant line consists of weighted means of the convex function (for ''t'' ∈ ,1, :t f(x_1) + (1-t) f(x_2), whil ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coding Theory
Coding theory is the study of the properties of codes and their respective fitness for specific applications. Codes are used for data compression, cryptography, error detection and correction, data transmission and data storage. Codes are studied by various scientific disciplines—such as information theory, electrical engineering, mathematics, linguistics, and computer science—for the purpose of designing efficient and reliable data transmission methods. This typically involves the removal of redundancy and the correction or detection of errors in the transmitted data. There are four types of coding: # Data compression (or ''source coding'') # Error control (or ''channel coding'') # Cryptographic coding # Line coding Data compression attempts to remove unwanted redundancy from the data from a source in order to transmit it more efficiently. For example, ZIP data compression makes data files smaller, for purposes such as to reduce Internet traffic. Data compression and er ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Information Theory
Information theory is the scientific study of the quantification, storage, and communication of information. The field was originally established by the works of Harry Nyquist and Ralph Hartley, in the 1920s, and Claude Shannon in the 1940s. The field is at the intersection of probability theory, statistics, computer science, statistical mechanics, information engineering, and electrical engineering. A key measure in information theory is entropy. Entropy quantifies the amount of uncertainty involved in the value of a random variable or the outcome of a random process. For example, identifying the outcome of a fair coin flip (with two equally likely outcomes) provides less information (lower entropy) than specifying the outcome from a roll of a die (with six equally likely outcomes). Some other important measures in information theory are mutual information, channel capacity, error exponents, and relative entropy. Important sub-fields of information theory include sourc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Log Sum Inequality
The log sum inequality is used for proving theorems in information theory. Statement Let a_1,\ldots,a_n and b_1,\ldots,b_n be nonnegative numbers. Denote the sum of all a_is by a and the sum of all b_is by b. The log sum inequality states that :\sum_^n a_i\log\frac\geq a\log\frac, with equality if and only if \frac are equal for all i, in other words a_i =c b_i for all i. (Take a_i\log \frac to be 0 if a_i=0 and \infty if a_i>0, b_i=0. These are the limiting values obtained as the relevant number tends to 0.) Proof Notice that after setting f(x)=x\log x we have : \begin \sum_^n a_i\log\frac & = \sum_^n b_i f\left(\frac\right) = b\sum_^n \frac f\left(\frac\right) \\ & \geq b f\left(\sum_^n \frac\frac\right) = b f\left(\frac\sum_^n a_i\right) = b f\left(\frac\right) \\ & = a\log\frac, \end where the inequality follows from Jensen's inequality since \frac\geq 0, \sum_^n\frac= 1, and f is convex. Generalizations The inequality remains valid for n=\infty provided that a<\ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Information Entropy
In information theory, the entropy of a random variable is the average level of "information", "surprise", or "uncertainty" inherent to the variable's possible outcomes. Given a discrete random variable X, which takes values in the alphabet \mathcal and is distributed according to p: \mathcal\to , 1/math>: \Eta(X) := -\sum_ p(x) \log p(x) = \mathbb \log p(X), where \Sigma denotes the sum over the variable's possible values. The choice of base for \log, the logarithm, varies for different applications. Base 2 gives the unit of bits (or " shannons"), while base ''e'' gives "natural units" nat, and base 10 gives units of "dits", "bans", or " hartleys". An equivalent definition of entropy is the expected value of the self-information of a variable. The concept of information entropy was introduced by Claude Shannon in his 1948 paper " A Mathematical Theory of Communication",PDF archived froherePDF archived frohere and is also referred to as Shannon entropy. Shannon's theory d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
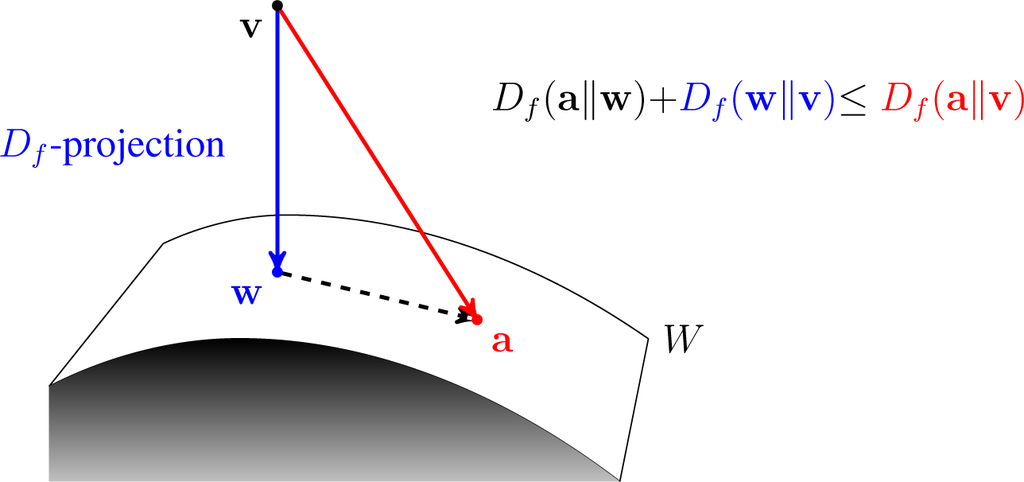
Bregman Divergence
In mathematics, specifically statistics and information geometry, a Bregman divergence or Bregman distance is a measure of difference between two points, defined in terms of a strictly convex function; they form an important class of divergences. When the points are interpreted as probability distributions – notably as either values of the parameter of a parametric model or as a data set of observed values – the resulting distance is a statistical distance. The most basic Bregman divergence is the squared Euclidean distance. Bregman divergences are similar to metrics, but satisfy neither the triangle inequality (ever) nor symmetry (in general). However, they satisfy a generalization of the Pythagorean theorem, and in information geometry the corresponding statistical manifold is interpreted as a (dually) flat manifold. This allows many techniques of optimization theory to be generalized to Bregman divergences, geometrically as generalizations of least squares. Bregman diverg ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Log Sum Inequality
The log sum inequality is used for proving theorems in information theory. Statement Let a_1,\ldots,a_n and b_1,\ldots,b_n be nonnegative numbers. Denote the sum of all a_is by a and the sum of all b_is by b. The log sum inequality states that :\sum_^n a_i\log\frac\geq a\log\frac, with equality if and only if \frac are equal for all i, in other words a_i =c b_i for all i. (Take a_i\log \frac to be 0 if a_i=0 and \infty if a_i>0, b_i=0. These are the limiting values obtained as the relevant number tends to 0.) Proof Notice that after setting f(x)=x\log x we have : \begin \sum_^n a_i\log\frac & = \sum_^n b_i f\left(\frac\right) = b\sum_^n \frac f\left(\frac\right) \\ & \geq b f\left(\sum_^n \frac\frac\right) = b f\left(\frac\sum_^n a_i\right) = b f\left(\frac\right) \\ & = a\log\frac, \end where the inequality follows from Jensen's inequality since \frac\geq 0, \sum_^n\frac= 1, and f is convex. Generalizations The inequality remains valid for n=\infty provided that a<\ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Surprisal
In information theory, the information content, self-information, surprisal, or Shannon information is a basic quantity derived from the probability of a particular Event (probability theory), event occurring from a random variable. It can be thought of as an alternative way of expressing probability, much like odds or log-odds, but which has particular mathematical advantages in the setting of information theory. The Shannon information can be interpreted as quantifying the level of "surprise" of a particular outcome. As it is such a basic quantity, it also appears in several other settings, such as the length of a message needed to transmit the event given an optimal Shannon's source coding theorem, source coding of the random variable. The Shannon information is closely related to ''Entropy (information theory), entropy'', which is the expected value of the self-information of a random variable, quantifying how surprising the random variable is "on average". This is the averag ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Information Theory
Information theory is the scientific study of the quantification, storage, and communication of information. The field was originally established by the works of Harry Nyquist and Ralph Hartley, in the 1920s, and Claude Shannon in the 1940s. The field is at the intersection of probability theory, statistics, computer science, statistical mechanics, information engineering, and electrical engineering. A key measure in information theory is entropy. Entropy quantifies the amount of uncertainty involved in the value of a random variable or the outcome of a random process. For example, identifying the outcome of a fair coin flip (with two equally likely outcomes) provides less information (lower entropy) than specifying the outcome from a roll of a die (with six equally likely outcomes). Some other important measures in information theory are mutual information, channel capacity, error exponents, and relative entropy. Important sub-fields of information theory include sourc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Logarithm
In mathematics, the logarithm is the inverse function to exponentiation. That means the logarithm of a number to the base is the exponent to which must be raised, to produce . For example, since , the ''logarithm base'' 10 of is , or . The logarithm of to ''base'' is denoted as , or without parentheses, , or even without the explicit base, , when no confusion is possible, or when the base does not matter such as in big O notation. The logarithm base is called the decimal or common logarithm and is commonly used in science and engineering. The natural logarithm has the number e (mathematical constant), as its base; its use is widespread in mathematics and physics, because of its very simple derivative. The binary logarithm uses base and is frequently used in computer science. Logarithms were introduced by John Napier in 1614 as a means of simplifying calculations. They were rapidly adopted by navigators, scientists, engineers, surveyors and oth ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kullback–Leibler Divergence
In mathematical statistics, the Kullback–Leibler divergence (also called relative entropy and I-divergence), denoted D_\text(P \parallel Q), is a type of statistical distance: a measure of how one probability distribution ''P'' is different from a second, reference probability distribution ''Q''. A simple interpretation of the KL divergence of ''P'' from ''Q'' is the expected excess surprise from using ''Q'' as a model when the actual distribution is ''P''. While it is a distance, it is not a metric, the most familiar type of distance: it is not symmetric in the two distributions (in contrast to variation of information), and does not satisfy the triangle inequality. Instead, in terms of information geometry, it is a type of divergence, a generalization of squared distance, and for certain classes of distributions (notably an exponential family), it satisfies a generalized Pythagorean theorem (which applies to squared distances). In the simple case, a relative entropy of 0 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |