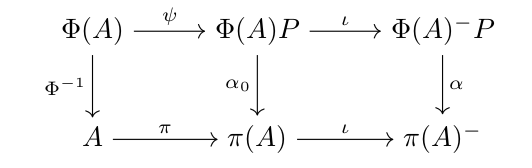|
Gelfand–Naimark–Segal Construction
In functional analysis, a discipline within mathematics, given a C*-algebra ''A'', the Gelfand–Naimark–Segal construction establishes a correspondence between cyclic *-representations of ''A'' and certain linear functionals on ''A'' (called ''states''). The correspondence is shown by an explicit construction of the *-representation from the state. It is named for Israel Gelfand, Mark Naimark, and Irving Segal. States and representations A *-representation of a C*-algebra ''A'' on a Hilbert space ''H'' is a mapping π from ''A'' into the algebra of bounded operators on ''H'' such that * π is a ring homomorphism which carries involution on ''A'' into involution on operators * π is nondegenerate, that is the space of vectors π(''x'') ξ is dense as ''x'' ranges through ''A'' and ξ ranges through ''H''. Note that if ''A'' has an identity, nondegeneracy means exactly π is unit-preserving, i.e. π maps the identity of ''A'' to the identity operator on ''H''. A state on a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Functional Analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure (e.g. inner product, norm, topology, etc.) and the linear functions defined on these spaces and respecting these structures in a suitable sense. The historical roots of functional analysis lie in the study of spaces of functions and the formulation of properties of transformations of functions such as the Fourier transform as transformations defining continuous, unitary etc. operators between function spaces. This point of view turned out to be particularly useful for the study of differential and integral equations. The usage of the word '' functional'' as a noun goes back to the calculus of variations, implying a function whose argument is a function. The term was first used in Hadamard's 1910 book on that subject. However, the general concept of a functional had previously been introduced in 1887 by the I ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convex Set
In geometry, a subset of a Euclidean space, or more generally an affine space over the reals, is convex if, given any two points in the subset, the subset contains the whole line segment that joins them. Equivalently, a convex set or a convex region is a subset that intersects every line into a single line segment (possibly empty). For example, a solid cube is a convex set, but anything that is hollow or has an indent, for example, a crescent shape, is not convex. The boundary of a convex set is always a convex curve. The intersection of all the convex sets that contain a given subset of Euclidean space is called the convex hull of . It is the smallest convex set containing . A convex function is a real-valued function defined on an interval with the property that its epigraph (the set of points on or above the graph of the function) is a convex set. Convex minimization is a subfield of optimization that studies the problem of minimizing convex functions over convex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Enveloping Von Neumann Algebra
In operator algebras, the enveloping von Neumann algebra of a C*-algebra is a von Neumann algebra that contains all the operator-algebraic information about the given C*-algebra. This may also be called the ''universal'' enveloping von Neumann algebra, since it is given by a universal property; and (as always with von Neumann algebras) the term ''W*-algebra'' may be used in place of ''von Neumann algebra''. Definition Let ''A'' be a C*-algebra and ''π''''U'' be its universal representation, acting on Hilbert space ''H''''U''. The image of ''π''''U'', ''π''''U''(''A''), is a C*-subalgebra of bounded operators on ''H''''U''. The enveloping von Neumann algebra of ''A'' is the closure of ''π''''U''(''A'') in the weak operator topology. It is sometimes denoted by ''A''′′. Properties The universal representation ''π''''U'' and ''A''′′ satisfies the following universal property: for any representation ''π'', there is a unique *-homomorph ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Weak Operator Topology
In functional analysis, the weak operator topology, often abbreviated WOT, is the weakest topology on the set of bounded operators on a Hilbert space H, such that the functional sending an operator T to the complex number \langle Tx, y\rangle is continuous for any vectors x and y in the Hilbert space. Explicitly, for an operator T there is base of neighborhoods of the following type: choose a finite number of vectors x_i, continuous functionals y_i, and positive real constants \varepsilon_i indexed by the same finite set I. An operator S lies in the neighborhood if and only if , y_i(T(x_i) - S(x_i)), 0. Relationships between different topologies on ''B(X,Y)'' The different terminology for the various topologies on B(X,Y) can sometimes be confusing. For instance, "strong convergence" for vectors in a normed space sometimes refers to norm-convergence, which is very often distinct from (and stronger than) than SOT-convergence when the normed space in question is B(X,Y). The wea ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Universal Representation (C*-algebra)
In the theory of C*-algebras, the universal representation of a C*-algebra is a faithful representation which is the direct sum of the GNS representations corresponding to the states of the C*-algebra. The various properties of the universal representation are used to obtain information about the ideals and quotients of the C*-algebra. The close relationship between an arbitrary representation of a C*-algebra and its universal representation can be exploited to obtain several criteria for determining whether a linear functional on the algebra is ultraweakly continuous. The method of using the properties of the universal representation as a tool to prove results about the C*-algebra and its representations is commonly referred to as ''universal representation techniques'' in the literature. Formal definition and properties :Definition. Let ''A'' be a C*-algebra with state space ''S''. The representation ::\Phi := \sum_ \oplus \; \pi_\rho :on the Hilbert space H_ is known as the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Faithful Functor
In category theory, a faithful functor is a functor that is injective on hom-sets, and a full functor is surjective on hom-sets. A functor that has both properties is called a full and faithful functor. Formal definitions Explicitly, let ''C'' and ''D'' be (locally small) categories and let ''F'' : ''C'' → ''D'' be a functor from ''C'' to ''D''. The functor ''F'' induces a function :F_\colon\mathrm_(X,Y)\rightarrow\mathrm_(F(X),F(Y)) for every pair of objects ''X'' and ''Y'' in ''C''. The functor ''F'' is said to be *faithful if ''F''''X'',''Y'' is injectiveJacobson (2009), p. 22 *full if ''F''''X'',''Y'' is surjectiveMac Lane (1971), p. 14 *fully faithful (= full and faithful) if ''F''''X'',''Y'' is bijective for each ''X'' and ''Y'' in ''C''. A mnemonic for remembering the term "full" is that the image of the function fills the codomain; a mnemonic for remembering the term "faithful" is that you can trust (have faith) that F(X)=F(Y) implies X=Y. Properties A faithful fun ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gelfand–Naimark Theorem
In mathematics, the Gelfand–Naimark theorem states that an arbitrary C*-algebra ''A'' is isometrically *-isomorphic to a C*-subalgebra of bounded operators on a Hilbert space. This result was proven by Israel Gelfand and Mark Naimark in 1943 and was a significant point in the development of the theory of C*-algebras since it established the possibility of considering a C*-algebra as an abstract algebraic entity without reference to particular realizations as an operator algebra. Details The Gelfand–Naimark representation π is the direct sum of representations π''f'' of ''A'' where ''f'' ranges over the set of pure states of A and π''f'' is the irreducible representation associated to ''f'' by the GNS construction. Thus the Gelfand–Naimark representation acts on the Hilbert direct sum of the Hilbert spaces ''H''''f'' by : \pi(x) bigoplus_ H_f= \bigoplus_ \pi_f(x)H_f. π(''x'') is a bounded linear operator since it is the direct sum of a family of operators, each ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Approximate Identity
In mathematics, particularly in functional analysis and ring theory, an approximate identity is a net in a Banach algebra or ring (generally without an identity) that acts as a substitute for an identity element. Definition A right approximate identity in a Banach algebra ''A'' is a net \ such that for every element ''a'' of ''A'', \lim_\lVert ae_\lambda - a \rVert = 0. Similarly, a left approximate identity in a Banach algebra ''A'' is a net \ such that for every element ''a'' of ''A'', \lim_\lVert e_\lambda a - a \rVert = 0. An approximate identity is a net which is both a right approximate identity and a left approximate identity. C*-algebras For C*-algebras, a right (or left) approximate identity consisting of self-adjoint elements is the same as an approximate identity. The net of all positive elements in ''A'' of norm ≤ 1 with its natural order is an approximate identity for any C*-algebra. This is called the canonical approximate identity of a C*-algebra. Ap ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Adjoint
In mathematics, the term ''adjoint'' applies in several situations. Several of these share a similar formalism: if ''A'' is adjoint to ''B'', then there is typically some formula of the type :(''Ax'', ''y'') = (''x'', ''By''). Specifically, adjoint or adjunction may mean: * Adjoint of a linear map, also called its transpose * Hermitian adjoint (adjoint of a linear operator) in functional analysis * Adjoint endomorphism of a Lie algebra * Adjoint representation of a Lie group * Adjoint functors in category theory * Adjunction (field theory) * Adjunction formula (algebraic geometry) * Adjunction space in topology * Conjugate transpose of a matrix in linear algebra * Adjugate matrix, related to its inverse * Adjoint equation * The upper and lower adjoints of a Galois connection in order theory * The adjoint of a differential operator with general polynomial coefficients * Kleisli adjunction * Monoidal adjunction * Quillen adjunction * Axiom of adjunction In mathematical set theor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cauchy Completion
In mathematical analysis, a metric space is called complete (or a Cauchy space) if every Cauchy sequence of points in has a limit that is also in . Intuitively, a space is complete if there are no "points missing" from it (inside or at the boundary). For instance, the set of rational numbers is not complete, because e.g. \sqrt is "missing" from it, even though one can construct a Cauchy sequence of rational numbers that converges to it (see further examples below). It is always possible to "fill all the holes", leading to the ''completion'' of a given space, as explained below. Definition Cauchy sequence A sequence x_1, x_2, x_3, \ldots in a metric space (X, d) is called Cauchy if for every positive real number r > 0 there is a positive integer N such that for all positive integers m, n > N, d\left(x_m, x_n\right) < r. Complete space A metric space is complete if any of the following equivalent conditions are satisfied: :#Every |
Quotient Space (linear Algebra)
In linear algebra, the quotient of a vector space ''V'' by a subspace ''N'' is a vector space obtained by "collapsing" ''N'' to zero. The space obtained is called a quotient space and is denoted ''V''/''N'' (read "''V'' mod ''N''" or "''V'' by ''N''"). Definition Formally, the construction is as follows. Let ''V'' be a vector space over a field ''K'', and let ''N'' be a subspace of ''V''. We define an equivalence relation ~ on ''V'' by stating that ''x'' ~ ''y'' if . That is, ''x'' is related to ''y'' if one can be obtained from the other by adding an element of ''N''. From this definition, one can deduce that any element of ''N'' is related to the zero vector; more precisely, all the vectors in ''N'' get mapped into the equivalence class of the zero vector. The equivalence class – or, in this case, the coset – of ''x'' is often denoted : 'x''= ''x'' + ''N'' since it is given by : 'x''= . The quotient space ''V''/''N'' is then defined as ''V''/~, the set of all equival ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |