|
Fractional Calculus
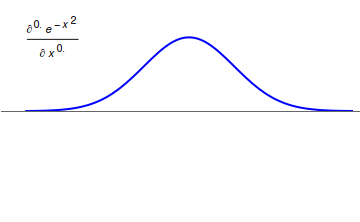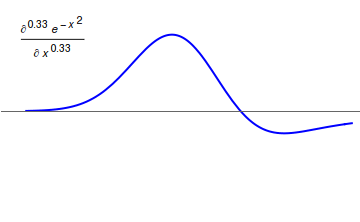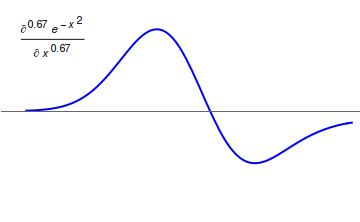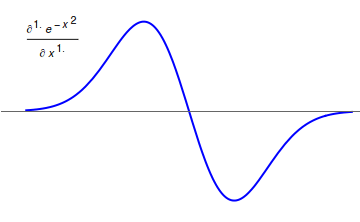
Fractional calculus is a branch of mathematical analysis that studies the several different possibilities of defining real number powers or complex number powers of the differentiation operator D :D f(x) = \frac f(x)\,, and of the integration operator J The symbol J is commonly used instead of the intuitive I in order to avoid confusion with other concepts identified by similar I–like glyphs, such as identities. :J f(x) = \int_0^x f(s) \,ds\,, and developing a calculus for such operators generalizing the classical one. In this context, the term ''powers'' refers to iterative application of a linear operator D to a function f, that is, repeatedly composing D with itself, as in D^n(f) = (\underbrace_n)(f) = \underbrace_n (f)\cdots))). For example, one may ask for a meaningful interpretation of :\sqrt = D^\frac12 as an analogue of the functional square root for the differentiation operator, that is, an expression for some linear operator that, when applied ''twice'' to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Analysis
Analysis is the branch of mathematics dealing with continuous functions, limit (mathematics), limits, and related theories, such as Derivative, differentiation, Integral, integration, measure (mathematics), measure, infinite sequences, series (mathematics), series, and analytic functions. These theories are usually studied in the context of Real number, real and Complex number, complex numbers and Function (mathematics), functions. Analysis evolved from calculus, which involves the elementary concepts and techniques of analysis. Analysis may be distinguished from geometry; however, it can be applied to any Space (mathematics), space of mathematical objects that has a definition of nearness (a topological space) or specific distances between objects (a metric space). History Ancient Mathematical analysis formally developed in the 17th century during the Scientific Revolution, but many of its ideas can be traced back to earlier mathematicians. Early results in analysis were i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Differential Equation
In mathematics, a differential equation is an equation that relates one or more unknown functions and their derivatives. In applications, the functions generally represent physical quantities, the derivatives represent their rates of change, and the differential equation defines a relationship between the two. Such relations are common; therefore, differential equations play a prominent role in many disciplines including engineering, physics, economics, and biology. Mainly the study of differential equations consists of the study of their solutions (the set of functions that satisfy each equation), and of the properties of their solutions. Only the simplest differential equations are solvable by explicit formulas; however, many properties of solutions of a given differential equation may be determined without computing them exactly. Often when a closed-form expression for the solutions is not available, solutions may be approximated numerically using computers. The theory of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gamma Function
In mathematics, the gamma function (represented by , the capital letter gamma from the Greek alphabet) is one commonly used extension of the factorial function to complex numbers. The gamma function is defined for all complex numbers except the non-positive integers. For every positive integer , \Gamma(n) = (n-1)!\,. Derived by Daniel Bernoulli, for complex numbers with a positive real part, the gamma function is defined via a convergent improper integral: \Gamma(z) = \int_0^\infty t^ e^\,dt, \ \qquad \Re(z) > 0\,. The gamma function then is defined as the analytic continuation of this integral function to a meromorphic function that is holomorphic in the whole complex plane except zero and the negative integers, where the function has simple poles. The gamma function has no zeroes, so the reciprocal gamma function is an entire function. In fact, the gamma function corresponds to the Mellin transform of the negative exponential function: \Gamma(z) = \mathcal M ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cauchy Formula For Repeated Integration
The Cauchy formula for repeated integration, named after Augustin-Louis Cauchy, allows one to compress ''n'' antidifferentiations of a function into a single integral (cf. Cauchy's formula). Scalar case Let ''f'' be a continuous function on the real line. Then the ''n''th repeated integral of ''f'' with basepoint ''a'', f^(x) = \int_a^x \int_a^ \cdots \int_a^ f(\sigma_) \, \mathrm\sigma_ \cdots \, \mathrm\sigma_2 \, \mathrm\sigma_1, is given by single integration f^(x) = \frac \int_a^x\left(x-t\right)^ f(t)\,\mathrmt. Proof A proof is given by induction. The base case with ''n=1'' is trivial, since it is equivalent to: f^(x) = \frac1\int_a^x f(t)\,\mathrmt = \int_a^x f(t)\,\mathrmtNow, suppose this is true for ''n'', and let us prove it for ''n''+1. Firstly, using the Leibniz integral rule, note that \frac \left \frac \int_a^x \left(x-t\right)^n f(t)\,\mathrmt \right= \frac \int_a^x\left(x-t\right)^ f(t)\,\mathrmt . Then, applying the induction hypothesis, \begin f^(x) &= \int ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mellin Transform
In mathematics, the Mellin transform is an integral transform that may be regarded as the multiplicative version of the two-sided Laplace transform. This integral transform is closely connected to the theory of Dirichlet series, and is often used in number theory, mathematical statistics, and the theory of asymptotic expansions; it is closely related to the Laplace transform and the Fourier transform, and the theory of the gamma function and allied special functions. The Mellin transform of a function is :\left\(s) = \varphi(s)=\int_0^\infty x^ f(x) \, dx. The inverse transform is :\left\(x) = f(x)=\frac \int_^ x^ \varphi(s)\, ds. The notation implies this is a line integral taken over a vertical line in the complex plane, whose real part ''c'' need only satisfy a mild lower bound. Conditions under which this inversion is valid are given in the Mellin inversion theorem. The transform is named after the Finnish mathematician Hjalmar Mellin, who introduced it in a paper pu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fourier Transform
A Fourier transform (FT) is a mathematical transform that decomposes functions into frequency components, which are represented by the output of the transform as a function of frequency. Most commonly functions of time or space are transformed, which will output a function depending on temporal frequency or spatial frequency respectively. That process is also called ''analysis''. An example application would be decomposing the waveform of a musical chord into terms of the intensity of its constituent pitches. The term ''Fourier transform'' refers to both the frequency domain representation and the mathematical operation that associates the frequency domain representation to a function of space or time. The Fourier transform of a function is a complex-valued function representing the complex sinusoids that comprise the original function. For each frequency, the magnitude ( absolute value) of the complex value represents the amplitude of a constituent complex sinusoid ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Boundary Condition
In mathematics, in the field of differential equations, a boundary value problem is a differential equation together with a set of additional constraints, called the boundary conditions. A solution to a boundary value problem is a solution to the differential equation which also satisfies the boundary conditions. Boundary value problems arise in several branches of physics as any physical differential equation will have them. Problems involving the wave equation, such as the determination of normal modes, are often stated as boundary value problems. A large class of important boundary value problems are the Sturm–Liouville problems. The analysis of these problems involves the eigenfunctions of a differential operator. To be useful in applications, a boundary value problem should be well posed. This means that given the input to the problem there exists a unique solution, which depends continuously on the input. Much theoretical work in the field of partial differential equ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Operational Calculus
Operational calculus, also known as operational analysis, is a technique by which problems in analysis, in particular differential equations, are transformed into algebraic problems, usually the problem of solving a polynomial equation. History The idea of representing the processes of calculus, differentiation and integration, as operators has a long history that goes back to Gottfried Wilhelm Leibniz. The mathematician Louis François Antoine Arbogast was one of the first to manipulate these symbols independently of the function to which they were applied. This approach was further developed by Francois-Joseph Servois who developed convenient notations. Servois was followed by a school of British and Irish mathematicians including Charles James Hargreave, George Boole, Bownin, Carmichael, Doukin, Graves, Murphy, William Spottiswoode and Sylvester. Treatises describing the application of operator methods to ordinary and partial differential equations were written by Robert ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Oliver Heaviside
Oliver Heaviside FRS (; 18 May 1850 – 3 February 1925) was an English self-taught mathematician and physicist who invented a new technique for solving differential equations (equivalent to the Laplace transform), independently developed vector calculus, and rewrote Maxwell's equations in the form commonly used today. He significantly shaped the way Maxwell's equations are understood and applied in the decades following Maxwell's death. His formulation of the telegrapher's equations became commercially important during his own lifetime, after their significance went unremarked for a long while, as few others were versed at the time in his novel methodology. Although at odds with the scientific establishment for most of his life, Heaviside changed the face of telecommunications, mathematics, and science. Biography Early life Heaviside was born in Camden Town, London, at 55 Kings Street (now Plender Street), the youngest of three children of Thomas, a draughtsman and wood ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Autodidact
Autodidacticism (also autodidactism) or self-education (also self-learning and self-teaching) is education without the guidance of masters (such as teachers and professors) or institutions (such as schools). Generally, autodidacts are individuals who choose the subject they will study, their studying material, and the studying rhythm and time. Autodidacts may or may not have formal education, and their study may be either a complement or an alternative to formal education. Many notable contributions have been made by autodidacts. Etymology The term has its roots in the Ancient Greek words (, ) and (, ). The related term '' didacticism'' defines an artistic philosophy of education. Terminology Various terms are used to describe self-education. One such is heutagogy, coined in 2000 by Stewart Hase and Chris Kenyon of Southern Cross University in Australia; others are ''self-directed learning'' and ''self-determined learning''. In the heutagogy paradigm, a learner should ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Liouville
Joseph Liouville (; ; 24 March 1809 – 8 September 1882) was a French mathematician and engineer. Life and work He was born in Saint-Omer in France on 24 March 1809. His parents were Claude-Joseph Liouville (an army officer) and Thérèse Liouville (née Balland). Liouville gained admission into the École Polytechnique in 1825 and graduated in 1827. Just like Augustin-Louis Cauchy before him, Liouville studied engineering at École des Ponts et Chaussées after graduating from the Polytechnique, but opted instead for a career in mathematics. After some years as an assistant at various institutions including the École Centrale Paris, he was appointed as professor at the École Polytechnique in 1838. He obtained a chair in mathematics at the Collège de France in 1850 and a chair in mechanics at the Faculté des Sciences in 1857. Besides his academic achievements, he was very talented in organisational matters. Liouville founded the ''Journal de Mathématiques Pures et Ap ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Niels Henrik Abel
Niels Henrik Abel ( , ; 5 August 1802 – 6 April 1829) was a Norwegian mathematician who made pioneering contributions in a variety of fields. His most famous single result is the first complete proof demonstrating the impossibility of solving the general quintic equation in radicals. This question was one of the outstanding open problems of his day, and had been unresolved for over 250 years. He was also an innovator in the field of elliptic functions, discoverer of Abelian functions. He made his discoveries while living in poverty and died at the age of 26 from tuberculosis. Most of his work was done in six or seven years of his working life. Regarding Abel, the French mathematician Charles Hermite said: "Abel has left mathematicians enough to keep them busy for five hundred years." Another French mathematician, Adrien-Marie Legendre, said: "What a head the young Norwegian has!" The Abel Prize in mathematics, originally proposed in 1899 to complement the Nobel Prizes (but ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |