|
Frobenius-Perron Operator
In mathematics, the transfer operator encodes information about an iterated map and is frequently used to study the behavior of dynamical systems, statistical mechanics, quantum chaos and fractals. In all usual cases, the largest eigenvalue is 1, and the corresponding eigenvector is the invariant measure of the system. The transfer operator is sometimes called the Ruelle operator, after David Ruelle, or the Perron–Frobenius operator or Ruelle–Perron–Frobenius operator, in reference to the applicability of the Perron–Frobenius theorem to the determination of the eigenvalues of the operator. Definition The iterated function to be studied is a map f\colon X\rightarrow X for an arbitrary set X. The transfer operator is defined as an operator \mathcal acting on the space of functions \ as :(\mathcal\Phi)(x) = \sum_ g(y) \Phi(y) where g\colon X\rightarrow\mathbb is an auxiliary valuation function. When f has a Jacobian determinant , J, , then g is usually taken to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Shift Operator
In mathematics, and in particular functional analysis, the shift operator, also known as the translation operator, is an operator that takes a function to its translation . In time series analysis, the shift operator is called the '' lag operator''. Shift operators are examples of linear operators, important for their simplicity and natural occurrence. The shift operator action on functions of a real variable plays an important role in harmonic analysis, for example, it appears in the definitions of almost periodic functions, positive-definite functions, derivatives, and convolution. Shifts of sequences (functions of an integer variable) appear in diverse areas such as Hardy spaces, the theory of abelian varieties, and the theory of symbolic dynamics, for which the baker's map is an explicit representation. The notion of triangulated category is a categorified analogue of the shift operator. Definition Functions of a real variable The shift operator (where ) takes a fu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Support (mathematics)
In mathematics, the support of a real-valued function f is the subset of the function domain of elements that are not mapped to zero. If the domain of f is a topological space, then the support of f is instead defined as the smallest closed set containing all points not mapped to zero. This concept is used widely in mathematical analysis. Formulation Suppose that f : X \to \R is a real-valued function whose domain is an arbitrary set X. The of f, written \operatorname(f), is the set of points in X where f is non-zero: \operatorname(f) = \. The support of f is the smallest subset of X with the property that f is zero on the subset's complement. If f(x) = 0 for all but a finite number of points x \in X, then f is said to have . If the set X has an additional structure (for example, a topology), then the support of f is defined in an analogous way as the smallest subset of X of an appropriate type such that f vanishes in an appropriate sense on its complement. The notion of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Ensemble
Quantum statistical mechanics is statistical mechanics applied to quantum mechanical systems. It relies on constructing density matrices that describe quantum systems in thermal equilibrium. Its applications include the study of collections of identical particles, which provides a theory that explains phenomena including superconductivity and superfluidity. Density matrices, expectation values, and entropy In quantum mechanics, probabilities for the outcomes of experiments made upon a system are calculated from the quantum state describing that system. Each physical system is associated with a vector space, or more specifically a Hilbert space. The dimension of the Hilbert space may be infinite, as it is for the space of square-integrable functions on a line, which is used to define the quantum physics of a continuous degree of freedom. Alternatively, the Hilbert space may be finite-dimensional, as occurs for spin degrees of freedom. A density operator, the mathematical rep ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hamiltonian (quantum Theory)
In quantum mechanics, the Hamiltonian of a system is an operator corresponding to the total energy of that system, including both kinetic energy and potential energy. Its spectrum, the system's ''energy spectrum'' or its set of ''energy eigenvalues'', is the set of possible outcomes obtainable from a measurement of the system's total energy. Due to its close relation to the energy spectrum and time-evolution of a system, it is of fundamental importance in most formulations of quantum theory. The Hamiltonian is named after William Rowan Hamilton, who developed a revolutionary reformulation of Newtonian mechanics, known as Hamiltonian mechanics, which was historically important to the development of quantum physics. Similar to vector notation, it is typically denoted by \hat, where the hat indicates that it is an operator. It can also be written as H or \check. Introduction The Hamiltonian of a system represents the total energy of the system; that is, the sum of the kineti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eigenfunction
In mathematics, an eigenfunction of a linear operator ''D'' defined on some function space is any non-zero function f in that space that, when acted upon by ''D'', is only multiplied by some scaling factor called an eigenvalue. As an equation, this condition can be written as Df = \lambda f for some scalar eigenvalue \lambda. The solutions to this equation may also be subject to boundary conditions that limit the allowable eigenvalues and eigenfunctions. An eigenfunction is a type of eigenvector. Eigenfunctions In general, an eigenvector of a linear operator ''D'' defined on some vector space is a nonzero vector in the domain of ''D'' that, when ''D'' acts upon it, is simply scaled by some scalar value called an eigenvalue. In the special case where ''D'' is defined on a function space, the eigenvectors are referred to as eigenfunctions. That is, a function ''f'' is an eigenfunction of ''D'' if it satisfies the equation where λ is a scalar. The solutions to Equation may also ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Molecular Dynamics
Molecular dynamics (MD) is a computer simulation method for analyzing the Motion (physics), physical movements of atoms and molecules. The atoms and molecules are allowed to interact for a fixed period of time, giving a view of the dynamics (mechanics), dynamic "evolution" of the system. In the most common version, the trajectory, trajectories of atoms and molecules are determined by Numerical integration, numerically solving Newton's laws of motion, Newton's equations of motion for a system of interacting particles, where Force (physics), forces between the particles and their potential energy, potential energies are often calculated using interatomic potentials or molecular mechanics, molecular mechanical Force field (chemistry), force fields. The method is applied mostly in chemical physics, materials science, and biophysics. Because molecular systems typically consist of a vast number of particles, it is impossible to determine the properties of such complex systems analyt ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
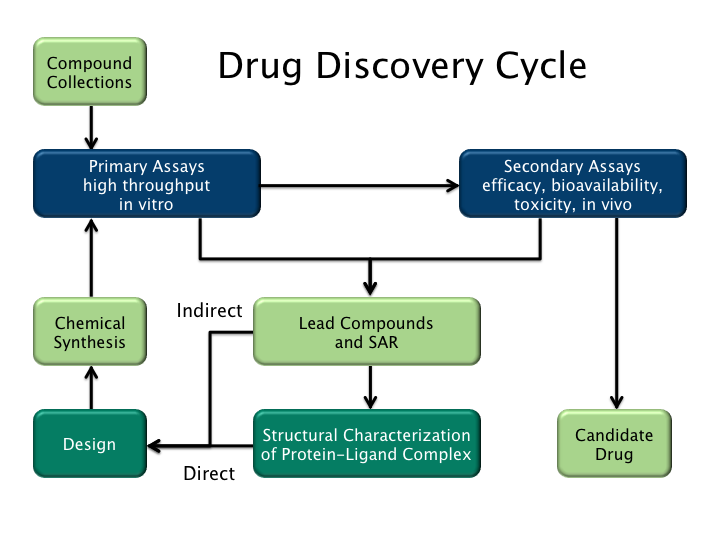
Rational Drug Design
Drug design, often referred to as rational drug design or simply rational design, is the invention, inventive process of finding new medications based on the knowledge of a biological target. The drug is most commonly an organic compound, organic small molecule that activates or inhibits the function of a biomolecule such as a protein, which in turn results in a therapeutic effect, therapeutic benefit to the patient. In the most basic sense, drug design involves the design of molecules that are complementary in shape and electric charge, charge to the biomolecular target with which they interact and therefore will bind to it. Drug design frequently but not necessarily relies on molecular modelling, computer modeling techniques. This type of modeling is sometimes referred to as computer-aided drug design. Finally, drug design that relies on the knowledge of the three-dimensional structure of the biomolecular target is known as structure-based drug design. In addition to small molec ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Physics
Physics is the scientific study of matter, its Elementary particle, fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge which relates to the order of nature, or, in other words, to the regular succession of events." It is one of the most fundamental scientific disciplines. "Physics is one of the most fundamental of the sciences. Scientists of all disciplines use the ideas of physics, including chemists who study the structure of molecules, paleontologists who try to reconstruct how dinosaurs walked, and climatologists who study how human activities affect the atmosphere and oceans. Physics is also the foundation of all engineering and technology. No engineer could design a flat-screen TV, an interplanetary spacecraft, or even a better mousetrap without first understanding the basic laws of physics. (...) You will come to see physics as a towering achievement of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chaos Theory
Chaos theory is an interdisciplinary area of Scientific method, scientific study and branch of mathematics. It focuses on underlying patterns and Deterministic system, deterministic Scientific law, laws of dynamical systems that are highly sensitive to initial conditions. These were once thought to have completely random states of disorder and irregularities. Chaos theory states that within the apparent randomness of chaotic complex systems, there are underlying patterns, interconnection, constant feedback loops, repetition, self-similarity, fractals and self-organization. The butterfly effect, an underlying principle of chaos, describes how a small change in one state of a deterministic nonlinear system can result in large differences in a later state (meaning there is sensitive dependence on initial conditions). A metaphor for this behavior is that a butterfly flapping its wings in Brazil can cause or prevent a tornado in Texas. Text was copied from this source, which is avai ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orthogonal Polynomials
In mathematics, an orthogonal polynomial sequence is a family of polynomials such that any two different polynomials in the sequence are orthogonal In mathematics, orthogonality (mathematics), orthogonality is the generalization of the geometric notion of ''perpendicularity''. Although many authors use the two terms ''perpendicular'' and ''orthogonal'' interchangeably, the term ''perpendic ... to each other under some inner product. The most widely used orthogonal polynomials are the classical orthogonal polynomials, consisting of the Hermite polynomials, the Laguerre polynomials and the Jacobi polynomials. The Gegenbauer polynomials form the most important class of Jacobi polynomials; they include the Chebyshev polynomials, and the Legendre polynomials as special cases. These are frequently given by the Rodrigues' formula. The field of orthogonal polynomials developed in the late 19th century from a study of continued fractions by Pafnuty Chebyshev, P. L. Chebyshev and wa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hessenberg Matrix
In linear algebra, a Hessenberg matrix is a special kind of square matrix, one that is "almost" triangular. To be exact, an upper Hessenberg matrix has zero entries below the first subdiagonal, and a lower Hessenberg matrix has zero entries above the first superdiagonal. They are named after Karl Hessenberg. A Hessenberg decomposition is a matrix decomposition of a matrix A into a unitary matrix P and a Hessenberg matrix H such that PHP^*=A where P^* denotes the conjugate transpose. Definitions Upper Hessenberg matrix A square n \times n matrix A is said to be in upper Hessenberg form or to be an upper Hessenberg matrix if a_=0 for all i,j with i > j+1. An upper Hessenberg matrix is called unreduced if all subdiagonal entries are nonzero, i.e. if a_ \neq 0 for all i \in \. Lower Hessenberg matrix A square n \times n matrix A is said to be in lower Hessenberg form or to be a lower Hessenberg matrix if its transpose is an upper Hessenberg matrix or equivalently if a_=0 for al ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |