 |
Elastic Pendulum
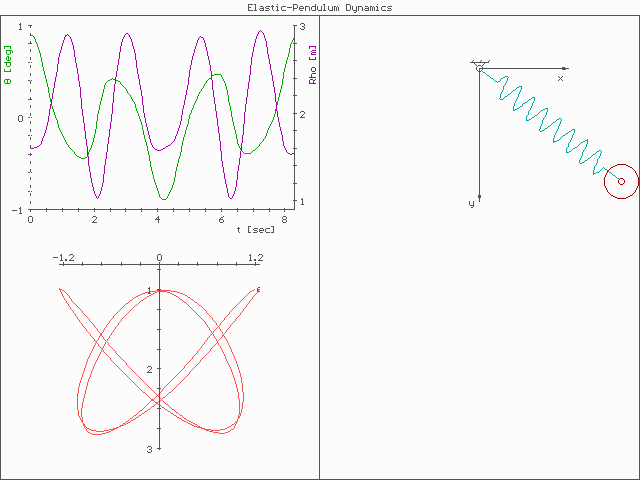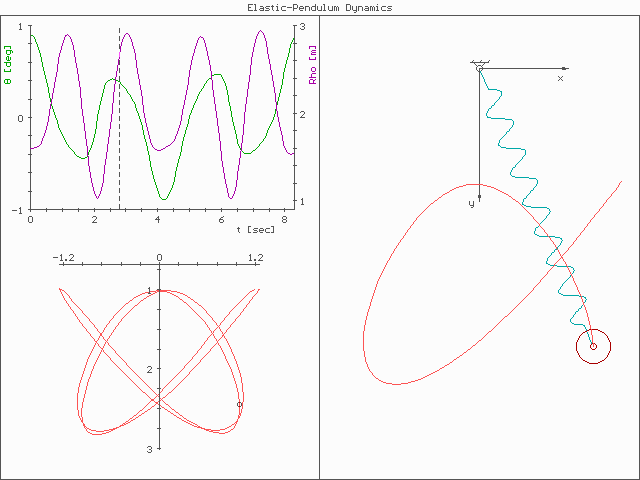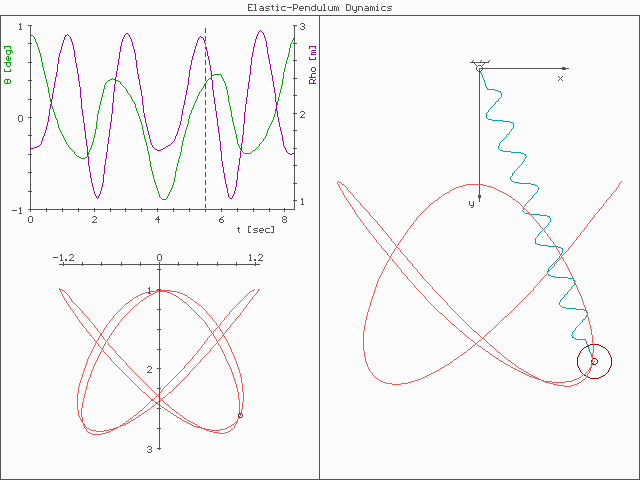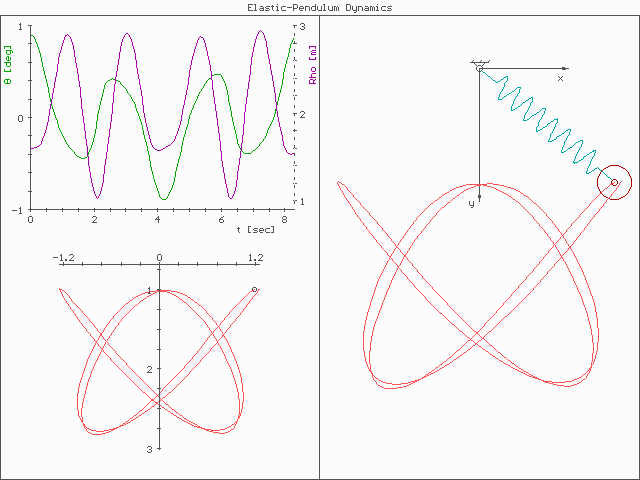
In physics and mathematics, in the area of dynamical systems, an elastic pendulum (also called spring pendulum or swinging spring) is a physical system where a piece of mass is connected to a spring so that the resulting motion contains elements of both a simple pendulum and a one-dimensional spring-mass system. For specific energy values, the system demonstrates all the hallmarks of chaotic behavior and is sensitive to initial conditions.At very low and very high energy, there also appears to be regular motion. The motion of an elastic pendulum is governed by a set of coupled ordinary differential equations.This behavior suggests a complex interplay between energy states and system dynamics. Analysis and interpretation The system is much more complex than a simple pendulum, as the properties of the spring add an extra dimension of freedom to the system. For example, when the spring compresses, the shorter radius causes the spring to move faster due to the conservat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
Spring-mass System
In classical mechanics, a harmonic oscillator is a system that, when displaced from its equilibrium position, experiences a restoring force ''F'' proportional to the displacement ''x'': \vec F = -k \vec x, where ''k'' is a positive constant. The harmonic oscillator model is important in physics, because any mass subject to a force in stable equilibrium acts as a harmonic oscillator for small vibrations. Harmonic oscillators occur widely in nature and are exploited in many manmade devices, such as clocks and radio circuits. If ''F'' is the only force acting on the system, the system is called a simple harmonic oscillator, and it undergoes simple harmonic motion: sinusoidal oscillations about the equilibrium point, with a constant amplitude and a constant frequency (which does not depend on the amplitude). If a frictional force (damping) proportional to the velocity is also present, the harmonic oscillator is described as a damped oscillator. Depending on the friction coeffi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
|
System Dynamics
System dynamics (SD) is an approach to understanding the nonlinear behaviour of complex systems over time using stocks, flows, internal feedback loops, table functions and time delays. Overview System dynamics is a methodology and mathematical modeling technique to frame, understand, and discuss complex issues and problems. Originally developed in the 1950s to help corporate managers improve their understanding of industrial processes, SD is currently being used throughout the public and private sector for policy analysis and design. Convenient graphical user interface (GUI) system dynamics software developed into user friendly versions by the 1990s and have been applied to diverse systems. SD models solve the problem of simultaneity (mutual causation) by updating all variables in small time increments with positive and negative feedbacks and time delays structuring the interactions and control. The best known SD model is probably the 1972 ''The Limits to Growth''. This model fo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
|
Ordinary Differential Equations
In mathematics, an ordinary differential equation (ODE) is a differential equation (DE) dependent on only a single independent variable. As with any other DE, its unknown(s) consists of one (or more) function(s) and involves the derivatives of those functions. The term "ordinary" is used in contrast with ''partial'' differential equations (PDEs) which may be with respect to one independent variable, and, less commonly, in contrast with ''stochastic'' differential equations (SDEs) where the progression is random. Differential equations A linear differential equation is a differential equation that is defined by a linear polynomial in the unknown function and its derivatives, that is an equation of the form :a_0(x)y +a_1(x)y' + a_2(x)y'' +\cdots +a_n(x)y^+b(x)=0, where a_0(x),\ldots,a_n(x) and b(x) are arbitrary differentiable functions that do not need to be linear, and y',\ldots, y^ are the successive derivatives of the unknown function y of the variable x. Among ord ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
|
Nondimensionalization
Nondimensionalization is the partial or full removal of physical dimensions from an equation involving physical quantities by a suitable substitution of variables. This technique can simplify and parameterize problems where measured units are involved. It is closely related to dimensional analysis. In some physical systems, the term ''scaling'' is used interchangeably with ''nondimensionalization'', in order to suggest that certain quantities are better measured relative to some appropriate unit. These units refer to quantities intrinsic to the system, rather than units such as SI units. Nondimensionalization is not the same as converting extensive quantities in an equation to intensive quantities, since the latter procedure results in variables that still carry units. Nondimensionalization can also recover characteristic properties of a system. For example, if a system has an intrinsic resonance frequency, length, or time constant, nondimensionalization can recover these ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
|
Degrees Of Freedom
In many scientific fields, the degrees of freedom of a system is the number of parameters of the system that may vary independently. For example, a point in the plane has two degrees of freedom for translation: its two coordinates; a non-infinitesimal object on the plane might have additional degrees of freedoms related to its orientation. In mathematics, this notion is formalized as the dimension of a manifold or an algebraic variety Algebraic varieties are the central objects of study in algebraic geometry, a sub-field of mathematics. Classically, an algebraic variety is defined as the solution set, set of solutions of a system of polynomial equations over the real number, .... When ''degrees of freedom'' is used instead of ''dimension'', this usually means that the manifold or variety that models the system is only implicitly defined. See: * Degrees of freedom (mechanics), number of independent motions that are allowed to the body or, in case of a mechanism made of seve ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
|
Velocity
Velocity is a measurement of speed in a certain direction of motion. It is a fundamental concept in kinematics, the branch of classical mechanics that describes the motion of physical objects. Velocity is a vector (geometry), vector Physical quantity, quantity, meaning that both magnitude and direction are needed to define it. The Scalar (physics), scalar absolute value (Magnitude (mathematics), magnitude) of velocity is called , being a coherent derived unit whose quantity is measured in the International System of Units, SI (metric system) as metres per second (m/s or m⋅s−1). For example, "5 metres per second" is a scalar, whereas "5 metres per second east" is a vector. If there is a change in speed, direction or both, then the object is said to be undergoing an ''acceleration''. Definition Average velocity The average velocity of an object over a period of time is its Displacement (geometry), change in position, \Delta s, divided by the duration of the period, \Delt ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
|
Gravitational Acceleration
In physics, gravitational acceleration is the acceleration of an object in free fall within a vacuum (and thus without experiencing drag (physics), drag). This is the steady gain in speed caused exclusively by gravitational attraction. All bodies accelerate in vacuum at the same rate, regardless of the masses or compositions of the bodies; the measurement and analysis of these rates is known as gravimetry. At a fixed point on the surface, the magnitude of gravity of Earth, Earth's gravity results from combined effect of gravitation and the centrifugal force from Earth's rotation. At different points on Earth's surface, the free fall acceleration ranges from , depending on altitude, latitude, and longitude. A conventional standard gravity, standard value is defined exactly as 9.80665 m/s² (about 32.1740 ft/s²). Locations of significant variation from this value are known as gravity anomaly, gravity anomalies. This does not take into account other effects, such as buoyancy or d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
 |
Gravity
In physics, gravity (), also known as gravitation or a gravitational interaction, is a fundamental interaction, a mutual attraction between all massive particles. On Earth, gravity takes a slightly different meaning: the observed force between objects and the Earth. This force is dominated by the combined gravitational interactions of particles but also includes effect of the Earth's rotation. Gravity gives weight to physical objects and is essential to understanding the mechanisms responsible for surface water waves and lunar tides. Gravity also has many important biological functions, helping to guide the growth of plants through the process of gravitropism and influencing the circulation of fluids in multicellular organisms. The gravitational attraction between primordial hydrogen and clumps of dark matter in the early universe caused the hydrogen gas to coalesce, eventually condensing and fusing to form stars. At larger scales this results in galaxies and clust ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
 |
Hooke's Law
In physics, Hooke's law is an empirical law which states that the force () needed to extend or compress a spring by some distance () scales linearly with respect to that distance—that is, where is a constant factor characteristic of the spring (i.e., its stiffness), and is small compared to the total possible deformation of the spring. The law is named after 17th-century British physicist Robert Hooke. He first stated the law in 1676 as a Latin anagram. He published the solution of his anagram in 1678 as: ("as the extension, so the force" or "the extension is proportional to the force"). Hooke states in the 1678 work that he was aware of the law since 1660. Hooke's equation holds (to some extent) in many other situations where an elastic body is deformed, such as wind blowing on a tall building, and a musician plucking a string of a guitar. An elastic body or material for which this equation can be assumed is said to be linear-elastic or Hookean. Hooke's law is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
 |
Potential Energy
In physics, potential energy is the energy of an object or system due to the body's position relative to other objects, or the configuration of its particles. The energy is equal to the work done against any restoring forces, such as gravity or those in a spring. The term ''potential energy'' was introduced by the 19th-century Scottish engineer and physicist William Rankine, although it has links to the ancient Greek philosopher Aristotle's concept of Potentiality and Actuality, ''potentiality''. Common types of potential energy include gravitational potential energy, the elastic potential energy of a deformed spring, and the electric potential energy of an electric charge and an electric field. The unit for energy in the International System of Units (SI) is the joule (symbol J). Potential energy is associated with forces that act on a body in a way that the total Work (physics), work done by these forces on the body depends only on the initial and final positions of the b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
 |
Kinetic Energy
In physics, the kinetic energy of an object is the form of energy that it possesses due to its motion. In classical mechanics, the kinetic energy of a non-rotating object of mass ''m'' traveling at a speed ''v'' is \fracmv^2.Resnick, Robert and Halliday, David (1960) ''Physics'', Section 7-5, Wiley International Edition The kinetic energy of an object is equal to the work, or force ( F) in the direction of motion times its displacement ( s), needed to accelerate the object from rest to its given speed. The same amount of work is done by the object when decelerating from its current speed to a state of rest. The SI unit of energy is the joule, while the English unit of energy is the foot-pound. In relativistic mechanics, \fracmv^2 is a good approximation of kinetic energy only when ''v'' is much less than the speed of light. History and etymology The adjective ''kinetic'' has its roots in the Greek word κίνησις ''kinesis'', meaning "motion". The dichoto ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |