|
Division By Zero
In mathematics, division by zero is division (mathematics), division where the divisor (denominator) is 0, zero. Such a division can be formally expression (mathematics), expressed as \tfrac, where is the dividend (numerator). In ordinary arithmetic, the expression has no meaning, as there is no number that, when multiplied by , gives (assuming a \neq 0); thus, division by zero is undefined (mathematics), undefined. Since any number multiplied by zero is zero, the expression 0/0, \tfrac is also undefined; when it is the form of a limit (mathematics), limit, it is an Indeterminate form#Indeterminate form 0/0, indeterminate form. Historically, one of the earliest recorded references to the mathematical impossibility of assigning a value to \tfrac is contained in Anglo-Irish people, Anglo-Irish philosopher George Berkeley's criticism of infinitesimal calculus in 1734 in ''The Analyst'' ("ghosts of departed quantities"). There are mathematical structures in which \tfrac is define ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hyperbola One Over X
In mathematics, a hyperbola (; pl. hyperbolas or hyperbolae ; adj. hyperbolic ) is a type of smooth function, smooth plane curve, curve lying in a plane, defined by its geometric properties or by equations for which it is the solution set. A hyperbola has two pieces, called Component (graph theory), connected components or branches, that are mirror images of each other and resemble two infinite bow (weapon), bows. The hyperbola is one of the three kinds of conic section, formed by the intersection of a plane (mathematics), plane and a double cone (geometry), cone. (The other conic sections are the parabola and the ellipse. A circle is a special case of an ellipse.) If the plane intersects both halves of the double cone but does not pass through the apex of the cones, then the conic is a hyperbola. Hyperbolas arise in many ways: * as the curve representing the multiplicative inverse, reciprocal function y(x) = 1/x in the Cartesian coordinate system, Cartesian plane, * as the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Computer
A computer is a machine that can be programmed to Execution (computing), carry out sequences of arithmetic or logical operations (computation) automatically. Modern digital electronic computers can perform generic sets of operations known as Computer program, programs. These programs enable computers to perform a wide range of tasks. A computer system is a nominally complete computer that includes the Computer hardware, hardware, operating system (main software), and peripheral equipment needed and used for full operation. This term may also refer to a group of computers that are linked and function together, such as a computer network or computer cluster. A broad range of Programmable logic controller, industrial and Consumer electronics, consumer products use computers as control systems. Simple special-purpose devices like microwave ovens and remote controls are included, as are factory devices like industrial robots and computer-aided design, as well as general-purpose devi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elementary Algebra
Elementary algebra encompasses the basic concepts of algebra. It is often contrasted with arithmetic: arithmetic deals with specified numbers, whilst algebra introduces variables (quantities without fixed values). This use of variables entails use of algebraic notation and an understanding of the general rules of the operations introduced in arithmetic. Unlike abstract algebra, elementary algebra is not concerned with algebraic structures outside the realm of real and complex numbers. It is typically taught to secondary school students and builds on their understanding of arithmetic. The use of variables to denote quantities allows general relationships between quantities to be formally and concisely expressed, and thus enables solving a broader scope of problems. Many quantitative relationships in science and mathematics are expressed as algebraic equations. Algebraic notation Algebraic notation describes the rules and conventions for writing mathematical expressio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fractions
A fraction (from la, fractus, "broken") represents a part of a whole or, more generally, any number of equal parts. When spoken in everyday English, a fraction describes how many parts of a certain size there are, for example, one-half, eight-fifths, three-quarters. A ''common'', ''vulgar'', or ''simple'' fraction (examples: \tfrac and \tfrac) consists of a numerator, displayed above a line (or before a slash like ), and a non-zero denominator, displayed below (or after) that line. Numerators and denominators are also used in fractions that are not ''common'', including compound fractions, complex fractions, and mixed numerals. In positive common fractions, the numerator and denominator are natural numbers. The numerator represents a number of equal parts, and the denominator indicates how many of those parts make up a unit or a whole. The denominator cannot be zero, because zero parts can never make up a whole. For example, in the fraction , the numerator 3 indicates that the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Remainder
In mathematics, the remainder is the amount "left over" after performing some computation. In arithmetic, the remainder is the integer "left over" after dividing one integer by another to produce an integer quotient (integer division). In algebra of polynomials, the remainder is the polynomial "left over" after dividing one polynomial by another. The ''modulo operation'' is the operation that produces such a remainder when given a dividend and divisor. Alternatively, a remainder is also what is left after subtracting one number from another, although this is more precisely called the ''difference''. This usage can be found in some elementary textbooks; colloquially it is replaced by the expression "the rest" as in "Give me two dollars back and keep the rest." However, the term "remainder" is still used in this sense when a function is approximated by a series expansion, where the error expression ("the rest") is referred to as the remainder term. Integer division Given an inte ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Set (mathematics)
A set is the mathematical model for a collection of different things; a set contains '' elements'' or ''members'', which can be mathematical objects of any kind: numbers, symbols, points in space, lines, other geometrical shapes, variables, or even other sets. The set with no element is the empty set; a set with a single element is a singleton. A set may have a finite number of elements or be an infinite set. Two sets are equal if they have precisely the same elements. Sets are ubiquitous in modern mathematics. Indeed, set theory, more specifically Zermelo–Fraenkel set theory, has been the standard way to provide rigorous foundations for all branches of mathematics since the first half of the 20th century. History The concept of a set emerged in mathematics at the end of the 19th century. The German word for set, ''Menge'', was coined by Bernard Bolzano in his work ''Paradoxes of the Infinite''. Georg Cantor, one of the founders of set theory, gave the following defin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elementary Arithmetic
The operators in elementary arithmetic are addition, subtraction, multiplication, and division. The operators can be applied on both real numbers and imaginary numbers. Each kind of number is represented on a number line designated to the type. Digits Digits are the set of symbols used to represent numbers. In a numeral system, each digit represents a value. The Arabic numerals (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) are the most common set of symbols, and the most frequently used form of these digits is the Western style. A numeral system defines the value of all numbers that contain more than one digit, most often by adding the value of adjacent digits. The Hindu–Arabic numeral system includes positional notation to determine the value of any numeral. In this type of system, the increase in value of an additional digit includes one or more multiplications with the radix value and the result is added to the value of an adjacent digit. For example, with Arabic numerals, the radix ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
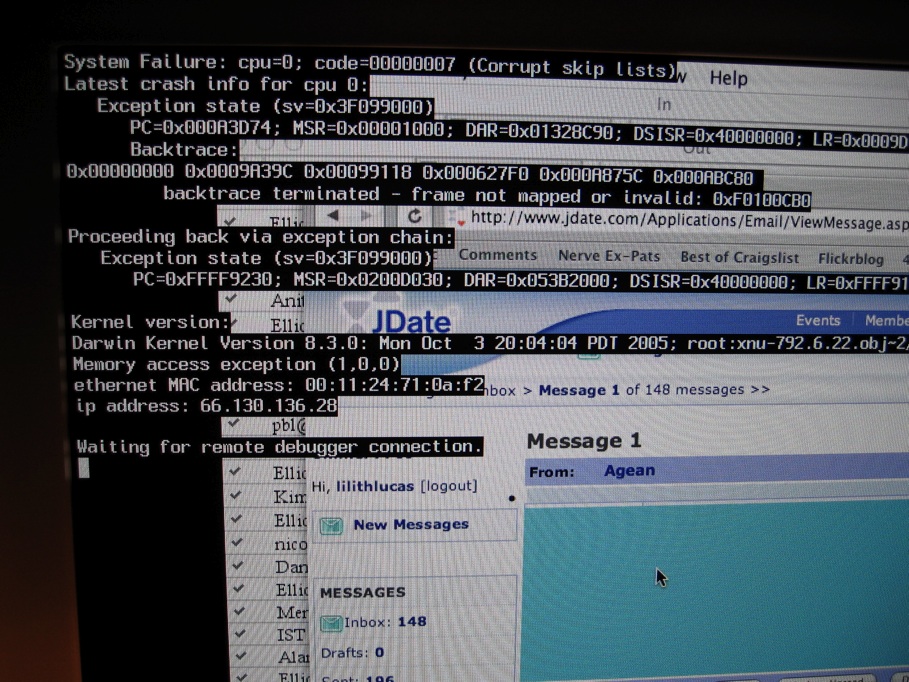
Crash (computing)
In computing, a crash, or system crash, occurs when a computer program such as a software application or an operating system stops functioning properly and exits. On some operating systems or individual applications, a crash reporting service will report the crash and any details relating to it (or give the user the option to do so), usually to the developer(s) of the application. If the program is a critical part of the operating system, the entire system may crash or hang, often resulting in a kernel panic or fatal system error. Most crashes are the result of a software bug. Typical causes include accessing invalid memory addresses, incorrect address values in the program counter, buffer overflow, overwriting a portion of the affected program code due to an earlier bug, executing invalid machine instructions (an illegal opcode), or triggering an unhandled exception. The original software bug that started this chain of events is typically considered to be the cause of the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Error Message
An error message is information displayed when an unforeseen occurs, usually on a computer or other device. On modern operating systems with graphical user interfaces, error messages are often displayed using dialog boxes. Error messages are used when user intervention is required, to indicate that a desired operation has failed, or to relay important warnings (such as warning a computer user that they are almost out of hard disk space). Error messages are seen widely throughout computing, and are part of every operating system or computer hardware device. Proper design of error messages is an important topic in usability and other fields of human–computer interaction. Common error messages The following error messages are commonly seen by modern computer users: ;Access denied :This error occurs if the user doesn't have privileges to a file, or if it has been locked by some program or user. ;Device not ready :This error most often occurs when there is no floppy disk (or a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Exception Handling
In computing and computer programming, exception handling is the process of responding to the occurrence of ''exceptions'' – anomalous or exceptional conditions requiring special processing – during the execution of a program. In general, an exception breaks the normal flow of execution and executes a pre-registered ''exception handler''; the details of how this is done depend on whether it is a hardware or software exception and how the software exception is implemented. Exception handling, if provided, is facilitated by specialized programming language constructs, hardware mechanisms like interrupts, or operating system (OS) inter-process communication (IPC) facilities like signals. Some exceptions, especially hardware ones, may be handled so gracefully that execution can resume where it was interrupted. Definition The definition of an exception is based on the observation that each procedure has a precondition, a set of circumstances for which it will terminate "normal ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
IEEE 754
The IEEE Standard for Floating-Point Arithmetic (IEEE 754) is a technical standard for floating-point arithmetic established in 1985 by the Institute of Electrical and Electronics Engineers (IEEE). The standard addressed many problems found in the diverse floating-point implementations that made them difficult to use reliably and portably. Many hardware floating-point units use the IEEE 754 standard. The standard defines: * ''arithmetic formats:'' sets of binary and decimal floating-point data, which consist of finite numbers (including signed zeros and subnormal numbers), infinities, and special "not a number" values (NaNs) * ''interchange formats:'' encodings (bit strings) that may be used to exchange floating-point data in an efficient and compact form * ''rounding rules:'' properties to be satisfied when rounding numbers during arithmetic and conversions * ''operations:'' arithmetic and other operations (such as trigonometric functions) on arithmetic formats * ''excepti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Extended Real Number Line
In mathematics, the affinely extended real number system is obtained from the real number system \R by adding two infinity elements: +\infty and -\infty, where the infinities are treated as actual numbers. It is useful in describing the algebra on infinities and the various limiting behaviors in calculus and mathematical analysis, especially in the theory of measure and integration. The affinely extended real number system is denoted \overline or \infty, +\infty/math> or It is the Dedekind–MacNeille completion of the real numbers. When the meaning is clear from context, the symbol +\infty is often written simply as Motivation Limits It is often useful to describe the behavior of a function f, as either the argument x or the function value f gets "infinitely large" in some sense. For example, consider the function f defined by :f(x) = \frac. The graph of this function has a horizontal asymptote at y = 0. Geometrically, when moving increasingly farther to the right along t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
.svg "Click for more on -> Hyperbola One Over X")
