|
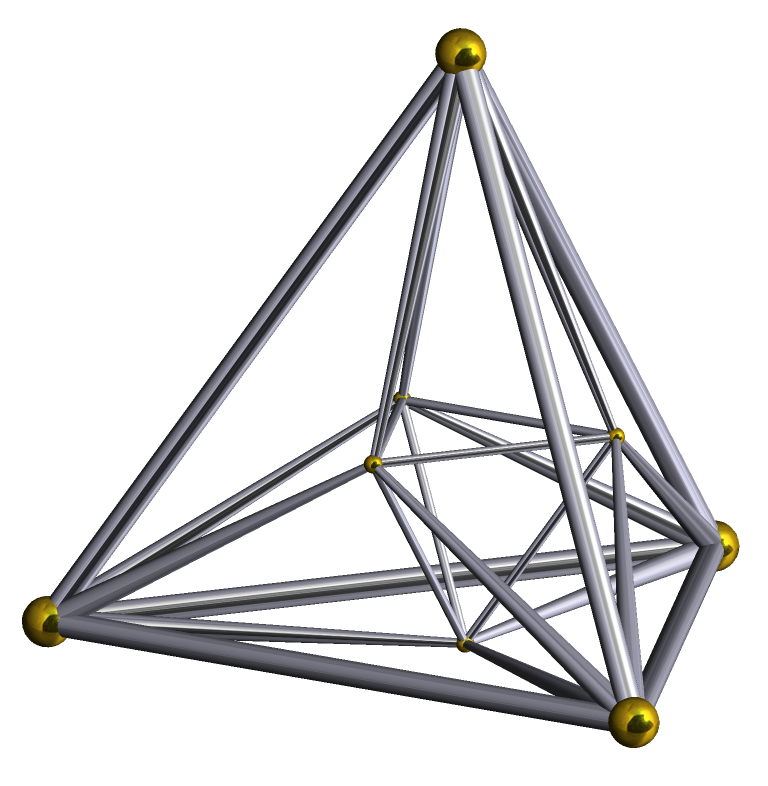
D4 Lattice
In four-dimensional Euclidean geometry, the 16-cell honeycomb is one of the three regular space-filling tessellations (or honeycombs), represented by Schläfli symbol , and constructed by a 4-dimensional packing of 16-cell facets, three around every face. Its dual is the 24-cell honeycomb. Its vertex figure is a 24-cell. The vertex arrangement is called the B4, D4, or F4 lattice. Alternate names * Hexadecachoric tetracomb/honeycomb * Demitesseractic tetracomb/honeycomb Coordinates Vertices can be placed at all integer coordinates (i,j,k,l), such that the sum of the coordinates is even. D4 lattice The vertex arrangement of the 16-cell honeycomb is called the D4 lattice or F4 lattice. The vertices of this lattice are the centers of the 3-spheres in the densest known packing of equal spheres in 4-space; its kissing number is 24, which is also the same as the kissing number in R4, as proved by Oleg Musin in 2003. The related D lattice (also called D) can be constructed by ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coxeter Group
In mathematics, a Coxeter group, named after H. S. M. Coxeter, is an abstract group that admits a formal description in terms of reflections (or kaleidoscopic mirrors). Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example. However, not all Coxeter groups are finite, and not all can be described in terms of symmetries and Euclidean reflections. Coxeter groups were introduced in 1934 as abstractions of reflection groups , and finite Coxeter groups were classified in 1935 . Coxeter groups find applications in many areas of mathematics. Examples of finite Coxeter groups include the symmetry groups of regular polytopes, and the Weyl groups of simple Lie algebras. Examples of infinite Coxeter groups include the triangle groups corresponding to regular tessellations of the Euclidean plane and the hyperbolic plane, and the Weyl groups of infinite-dimensional Kac–Moody algebras. Standa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vertex Arrangement
In geometry, a vertex arrangement is a set of points in space described by their relative positions. They can be described by their use in polytopes. For example, a ''square vertex arrangement'' is understood to mean four points in a plane, equal distance and angles from a center point. Two polytopes share the same ''vertex arrangement'' if they share the same 0-skeleton. A group of polytopes that shares a vertex arrangement is called an ''army''. Vertex arrangement The same set of vertices can be connected by edges in different ways. For example, the ''pentagon'' and ''pentagram'' have the same ''vertex arrangement'', while the second connects alternate vertices. A ''vertex arrangement'' is often described by the convex hull polytope which contains it. For example, the regular ''pentagram'' can be said to have a (regular) ''pentagonal vertex arrangement''. Infinite tilings can also share common ''vertex arrangements''. For example, this triangular lattice of points ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
24-cell Honeycomb
In Four-dimensional space, four-dimensional Euclidean geometry, the 24-cell honeycomb, or icositetrachoric honeycomb is a regular polytope, regular space-filling tessellation (or honeycomb (geometry), honeycomb) of 4-dimensional Euclidean space by regular 24-cells. It can be represented by Schläfli symbol . The dual polytope, dual tessellation by regular 16-cell honeycomb has Schläfli symbol . Together with the tesseractic honeycomb (or 4-cubic honeycomb) these are the only regular tessellations of Euclidean 4-space. Coordinates The 24-cell honeycomb can be constructed as the Voronoi tessellation of the D4 or F4 lattice, F4 root lattice. Each 24-cell is then centered at a D4 lattice point, i.e. one of :\left\. These points can also be described as Hurwitz quaternions with even square norm. The vertices of the honeycomb lie at the deep holes of the D4 lattice. These are the Hurwitz quaternions with odd square norm. It can be constructed as a #Symmetry constructions, birecti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Facet (mathematics)
In geometry, a facet is a feature of a polyhedron, polytope, or related geometric structure, generally of dimension one less than the structure itself. More specifically: * In three-dimensional geometry, a facet of a polyhedron is any polygon whose corners are vertices of the polyhedron, and is not a ''face''. To ''facet'' a polyhedron is to find and join such facets to form the faces of a new polyhedron; this is the reciprocal process to ''stellation'' and may also be applied to higher-dimensional polytopes. * In polyhedral combinatorics and in the general theory of polytopes, a facet (or hyperface) of a polytope of dimension ''n'' is a face that has dimension ''n'' − 1. Facets may also be called (''n'' − 1)-faces. In three-dimensional geometry, they are often called "faces" without qualification. * A facet of a simplicial complex is a maximal simplex, that is a simplex that is not a face of another simplex of the complex.. For (boundary complexes of) sim ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Honeycomb (geometry)
In geometry, a honeycomb is a ''space filling'' or '' close packing'' of polyhedral or higher-dimensional ''cells'', so that there are no gaps. It is an example of the more general mathematical ''tiling'' or ''tessellation'' in any number of dimensions. Its dimension can be clarified as ''n''-honeycomb for a honeycomb of ''n''-dimensional space. Honeycombs are usually constructed in ordinary Euclidean ("flat") space. They may also be constructed in non-Euclidean spaces, such as hyperbolic honeycombs. Any finite uniform polytope can be projected to its circumsphere to form a uniform honeycomb in spherical space. Classification There are infinitely many honeycombs, which have only been partially classified. The more regular ones have attracted the most interest, while a rich and varied assortment of others continue to be discovered. The simplest honeycombs to build are formed from stacked layers or ''slabs'' of prisms based on some tessellations of the plane. In particula ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tessellations
A tessellation or tiling is the covering of a surface, often a plane (mathematics), plane, using one or more geometric shapes, called ''tiles'', with no overlaps and no gaps. In mathematics, tessellation can be generalized to high-dimensional spaces, higher dimensions and a variety of geometries. A periodic tiling has a repeating pattern. Some special kinds include ''regular tilings'' with regular polygonal tiles all of the same shape, and ''semiregular tilings'' with regular tiles of more than one shape and with every corner identically arranged. The patterns formed by periodic tilings can be categorized into 17 wallpaper groups. A tiling that lacks a repeating pattern is called "non-periodic". An ''aperiodic tiling'' uses a small set of tile shapes that cannot form a repeating pattern. A ''tessellation of space'', also known as a space filling or honeycomb, can be defined in the geometry of higher dimensions. A real physical tessellation is a tiling made of materials such a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euclidean Geometry
Euclidean geometry is a mathematical system attributed to ancient Greek mathematician Euclid, which he described in his textbook on geometry: the '' Elements''. Euclid's approach consists in assuming a small set of intuitively appealing axioms (postulates) and deducing many other propositions (theorems) from these. Although many of Euclid's results had been stated earlier,. Euclid was the first to organize these propositions into a logical system in which each result is '' proved'' from axioms and previously proved theorems. The ''Elements'' begins with plane geometry, still taught in secondary school (high school) as the first axiomatic system and the first examples of mathematical proofs. It goes on to the solid geometry of three dimensions. Much of the ''Elements'' states results of what are now called algebra and number theory, explained in geometrical language. For more than two thousand years, the adjective "Euclidean" was unnecessary because no other sort of geometry ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Four-dimensional Space
A four-dimensional space (4D) is a mathematical extension of the concept of three-dimensional or 3D space. Three-dimensional space is the simplest possible abstraction of the observation that one only needs three numbers, called ''dimensions'', to describe the sizes or locations of objects in the everyday world. For example, the volume of a rectangular box is found by measuring and multiplying its length, width, and height (often labeled ''x'', ''y'', and ''z''). The idea of adding a fourth dimension began with Jean le Rond d'Alembert's "Dimensions" being published in 1754, was followed by Joseph-Louis Lagrange in the mid-1700s, and culminated in a precise formalization of the concept in 1854 by Bernhard Riemann. In 1880, Charles Howard Hinton popularized these insights in an essay titled " What is the Fourth Dimension?", which explained the concept of a " four-dimensional cube" with a step-by-step generalization of the properties of lines, squares, and cubes. The simplest fo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cell-transitive
In geometry, a tessellation of dimension (a plane tiling) or higher, or a polytope of dimension (a polyhedron) or higher, is isohedral or face-transitive if all its faces are the same. More specifically, all faces must be not merely congruent but must be ''transitive'', i.e. must lie within the same ''symmetry orbit''. In other words, for any two faces and , there must be a symmetry of the ''entire'' figure by translations, rotations, and/or reflections that maps onto . For this reason, convex isohedral polyhedra are the shapes that will make fair dice. Isohedral polyhedra are called isohedra. They can be described by their face configuration. An isohedron has an even number of faces. The dual of an isohedral polyhedron is vertex-transitive, i.e. isogonal. The Catalan solids, the bipyramids, and the trapezohedra are all isohedral. They are the duals of the (isogonal) Archimedean solids, prisms, and antiprisms, respectively. The Platonic solids, which are either s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Face-transitive
In geometry, a tessellation of dimension (a plane tiling) or higher, or a polytope of dimension (a polyhedron) or higher, is isohedral or face-transitive if all its faces are the same. More specifically, all faces must be not merely congruent but must be ''transitive'', i.e. must lie within the same ''symmetry orbit''. In other words, for any two faces and , there must be a symmetry of the ''entire'' figure by translations, rotations, and/or reflections that maps onto . For this reason, convex isohedral polyhedra are the shapes that will make fair dice. Isohedral polyhedra are called isohedra. They can be described by their face configuration. An isohedron has an even number of faces. The dual of an isohedral polyhedron is vertex-transitive, i.e. isogonal. The Catalan solids, the bipyramids, and the trapezohedra are all isohedral. They are the duals of the (isogonal) Archimedean solids, prisms, and antiprisms, respectively. The Platonic solids, which are either se ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |