|
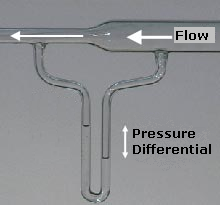
Dynamic Pressure
In fluid dynamics, dynamic pressure (denoted by or and sometimes called velocity pressure) is the quantity defined by:Clancy, L.J., ''Aerodynamics'', Section 3.5 :q = \frac\rho\, u^2 where (in SI units): * is the dynamic pressure in pascals (i.e., N/ m2), * (Greek letter rho) is the fluid mass density (e.g. in kg/m3), and * is the flow speed in m/s. It can be thought of as the fluid's kinetic energy per unit volume. For incompressible flow, the dynamic pressure of a fluid is the difference between its total pressure and static pressure. From Bernoulli's law, dynamic pressure is given by : p_0 - p_\text = \frac\rho\, u^2 where and are the total and static pressures, respectively. Physical meaning Dynamic pressure is the kinetic energy per unit volume of a fluid. Dynamic pressure is one of the terms of Bernoulli's equation, which can be derived from the conservation of energy for a fluid in motion. At a stagnation point the dynamic pressure is equal to the difference ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fluid Dynamics
In physics, physical chemistry and engineering, fluid dynamics is a subdiscipline of fluid mechanics that describes the flow of fluids – liquids and gases. It has several subdisciplines, including (the study of air and other gases in motion) and (the study of water and other liquids in motion). Fluid dynamics has a wide range of applications, including calculating forces and moment (physics), moments on aircraft, determining the mass flow rate of petroleum through pipeline transport, pipelines, weather forecasting, predicting weather patterns, understanding nebulae in interstellar space, understanding large scale Geophysical fluid dynamics, geophysical flows involving oceans/atmosphere and Nuclear weapon design, modelling fission weapon detonation. Fluid dynamics offers a systematic structure—which underlies these practical disciplines—that embraces empirical and semi-empirical laws derived from flow measurement and used to solve practical problems. The solution to a fl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Aerodynamics
Aerodynamics () is the study of the motion of atmosphere of Earth, air, particularly when affected by a solid object, such as an airplane wing. It involves topics covered in the field of fluid dynamics and its subfield of gas dynamics, and is an important domain of study in aeronautics. The term ''aerodynamics'' is often used synonymously with gas dynamics, the difference being that "gas dynamics" applies to the study of the motion of all gases, and is not limited to air. The formal study of aerodynamics began in the modern sense in the eighteenth century, although observations of fundamental concepts such as aerodynamic drag were recorded much earlier. Most of the early efforts in aerodynamics were directed toward achieving Aircraft#Heavier-than-air – aerodynes, heavier-than-air flight, which was first demonstrated by Otto Lilienthal in 1891. Since then, the use of aerodynamics through mathematical analysis, empirical approximations, wind tunnel experimentation, and computer si ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Standard Gravity
The standard acceleration of gravity or standard acceleration of free fall, often called simply standard gravity and denoted by or , is the nominal gravitational acceleration of an object in a vacuum near the surface of the Earth. It is a constant defined by standard as . This value was established by the third General Conference on Weights and Measures (1901, CR 70) and used to define the standard weight of an object as the product of its mass and this nominal acceleration. The acceleration of a body near the surface of the Earth is due to the combined effects of gravity and centrifugal acceleration from the rotation of the Earth (but the latter is small enough to be negligible for most purposes); the total (the apparent gravity) is about 0.5% greater at the poles than at the Equator. Although the symbol is sometimes used for standard gravity, (without a suffix) can also mean the local acceleration due to local gravity and centrifugal acceleration, which varies depending on on ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Incompressible Flow
In fluid mechanics, or more generally continuum mechanics, incompressible flow is a flow in which the material density does not vary over time. Equivalently, the divergence of an incompressible flow velocity is zero. Under certain conditions, the flow of compressible fluids can be modelled as incompressible flow to a good approximation. Derivation The fundamental requirement for incompressible flow is that the density, \rho , is constant within a small element volume, ''dV'', which moves at the flow velocity u. Mathematically, this constraint implies that the material derivative (discussed below) of the density must vanish to ensure incompressible flow. Before introducing this constraint, we must apply the conservation of mass to generate the necessary relations. The mass is calculated by a volume integral of the density, \rho : : = . The conservation of mass requires that the time derivative of the mass inside a control volume be equal to the mass flux, J, acro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Closed System
A closed system is a natural physical system that does not allow transfer of matter in or out of the system, althoughin the contexts of physics, chemistry, engineering, etc.the transfer of energy (e.g. as work or heat) is allowed. Physics In classical mechanics In nonrelativistic classical mechanics, a closed system is a physical system that does not exchange any matter with its surroundings, and is not subject to any net force whose source is external to the system. A closed system in classical mechanics would be equivalent to an isolated system in thermodynamics. Closed systems are often used to limit the factors that can affect the results of a specific problem or experiment. In thermodynamics In thermodynamics, a closed system can exchange energy (as heat or work) but not matter, with its surroundings. An isolated system cannot exchange any heat, work, or matter with the surroundings, while an open system can exchange energy and matter. (This scheme of definition of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
First Law Of Thermodynamics
The first law of thermodynamics is a formulation of the law of conservation of energy in the context of thermodynamic processes. For a thermodynamic process affecting a thermodynamic system without transfer of matter, the law distinguishes two principal forms of energy transfer, heat and thermodynamic work. The law also defines the internal energy of a system, an extensive property for taking account of the balance of heat transfer, thermodynamic work, and matter transfer, into and out of the system. Energy cannot be created or destroyed, but it can be transformed from one form to another. In an externally isolated system, with internal changes, the sum of all forms of energy is constant. An equivalent statement is that perpetual motion machines of the first kind are impossible; work done by a system on its surroundings requires that the system's internal energy be consumed, so that the amount of internal energy lost by that work must be resupplied as heat by an external e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bernoulli's Principle
Bernoulli's principle is a key concept in fluid dynamics that relates pressure, speed and height. For example, for a fluid flowing horizontally Bernoulli's principle states that an increase in the speed occurs simultaneously with a decrease in static pressure, pressure The principle is named after the Swiss mathematician and physicist Daniel Bernoulli, who published it in his book ''Hydrodynamica'' in 1738. Although Bernoulli deduced that pressure decreases when the flow speed increases, it was Leonhard Euler in 1752 who derived Bernoulli's equation in its usual form. Bernoulli's principle can be derived from the principle of conservation of energy. This states that, in a steady flow, the sum of all forms of energy in a fluid is the same at all points that are free of viscous forces. This requires that the sum of kinetic energy, potential energy and internal energy remains constant. Thus an increase in the speed of the fluid—implying an increase in its kinetic energy—occur ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hydraulic Head
Hydraulic head or piezometric head is a measurement related to liquid pressure (normalized by specific weight) and the liquid elevation above a vertical datum., 410 pages. See pp. 43–44., 650 pages. See p. 22, eq.3.2a. It is usually measured as an equivalent liquid surface elevation, expressed in units of length, at the entrance (or bottom) of a piezometer. In an aquifer, it can be calculated from the depth to water in a piezometric well (a specialized water well), and given information of the piezometer's elevation and screen depth. Hydraulic head can similarly be measured in a column of water using a standpipe piezometer by measuring the height of the water surface in the tube relative to a common datum. The hydraulic head can be used to determine a ''hydraulic gradient'' between two or more points. Definition In fluid dynamics, the ''head'' at some point in an incompressible (constant density) flow is equal to the height of a static column of fluid whose pressure at ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hydraulics
Hydraulics () is a technology and applied science using engineering, chemistry, and other sciences involving the mechanical properties and use of liquids. At a very basic level, hydraulics is the liquid counterpart of pneumatics, which concerns gases. Fluid mechanics provides the theoretical foundation for hydraulics, which focuses on applied engineering using the properties of fluids. In its fluid power applications, hydraulics is used for the generation, control, and transmission of Power (physics), power by the use of pressure, pressurized liquids. Hydraulic topics range through some parts of science and most of engineering modules, and they cover concepts such as pipe Volumetric flow rate, flow, dam design, fluidics, and fluid control circuitry. The principles of hydraulics are in use naturally in the human body within the vascular system and erectile tissue. ''Free surface hydraulics'' is the branch of hydraulics dealing with free surface flow, such as occurring in rivers ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Irrotational Flow
In fluid dynamics, potential flow or irrotational flow refers to a description of a fluid flow with no vorticity in it. Such a description typically arises in the limit of vanishing viscosity, i.e., for an inviscid fluid and with no vorticity present in the flow. Potential flow describes the velocity field as the gradient of a scalar function: the velocity potential. As a result, a potential flow is characterized by an irrotational velocity field, which is a valid approximation for several applications. The irrotationality of a potential flow is due to the curl of the gradient of a scalar always being equal to zero. In the case of an incompressible flow the velocity potential satisfies Laplace's equation, and potential theory is applicable. However, potential flows also have been used to describe compressible flows and Hele-Shaw flows. The potential flow approach occurs in the modeling of both stationary as well as nonstationary flows. Applications of potential flow include ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vector Calculus Identity
The following are important identities involving derivatives and integrals in vector calculus. Operator notation Gradient For a function f(x, y, z) in three-dimensional Cartesian coordinate variables, the gradient is the vector field: : \operatorname(f) = \nabla f = \begin\displaystyle \frac,\ \frac,\ \frac \end f = \frac \mathbf + \frac \mathbf + \frac \mathbf where i, j, k are the standard unit vectors for the ''x'', ''y'', ''z''-axes. More generally, for a function of ''n'' variables \psi(x_1, \ldots, x_n), also called a scalar field, the gradient is the vector field: \nabla\psi = \begin\displaystyle\frac, \ldots, \frac \end\psi = \frac \mathbf_1 + \dots + \frac\mathbf_n where \mathbf_ \, (i=1,2,..., n) are mutually orthogonal unit vectors. As the name implies, the gradient is proportional to, and points in the direction of, the function's most rapid (positive) change. For a vector field \mathbf = \left(A_1, \ldots, A_n\right), also called a tensor field ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |