|
Dirichlet's Test
In mathematics, Dirichlet's test is a method of testing for the convergence of a series that is especially useful for proving conditional convergence. It is named after its author Peter Gustav Lejeune Dirichlet, and was published posthumously in the '' Journal de Mathématiques Pures et Appliquées'' in 1862. Statement The test states that if (a_n) is a monotonic sequence of real numbers with \lim_ a_n = 0 and (b_n) is a sequence of real numbers or complex numbers with bounded partial sums, then the series :\sum_^ a_n b_n converges. Proof Let S_n = \sum_^n a_k b_k and B_n = \sum_^n b_k. From summation by parts, we have that S_n = a_ B_n + \sum_^ B_k (a_k - a_). Since the magnitudes of the partial sums B_n are bounded by some ''M'' and a_n \to 0 as n\to\infty, the first of these terms approaches zero: , a_ B_n, \leq , a_ M, \to 0 as n\to\infty. Furthermore, for each ''k'', , B_k (a_k - a_), \leq M, a_k - a_, . Since (a_n) is monotone, it is either decreasing or in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Telescoping Sum
In mathematics, a telescoping series is a series whose general term t_n is of the form t_n=a_-a_n, i.e. the difference of two consecutive terms of a sequence (a_n). As a consequence the partial sums of the series only consists of two terms of (a_n) after cancellation. The cancellation technique, with part of each term cancelling with part of the next term, is known as the method of differences. An early statement of the formula for the sum or partial sums of a telescoping series can be found in a 1644 work by Evangelista Torricelli, ''De dimensione parabolae''. Definition Telescoping sums are finite sums in which pairs of consecutive terms partly cancel each other, leaving only parts of the initial and final terms. Let a_n be the elements of a sequence of numbers. Then \sum_^N \left(a_n - a_\right) = a_N - a_0. If a_n converges to a limit L, the telescoping series gives: \sum_^\infty \left(a_n - a_\right) = L-a_0. Every series is a telescoping series of its own parti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Interval (mathematics)
In mathematics, a real interval is the set of all real numbers lying between two fixed endpoints with no "gaps". Each endpoint is either a real number or positive or negative infinity, indicating the interval extends without a bound. A real interval can contain neither endpoint, either endpoint, or both endpoints, excluding any endpoint which is infinite. For example, the set of real numbers consisting of , , and all numbers in between is an interval, denoted and called the unit interval; the set of all positive real numbers is an interval, denoted ; the set of all real numbers is an interval, denoted ; and any single real number is an interval, denoted . Intervals are ubiquitous in mathematical analysis. For example, they occur implicitly in the epsilon-delta definition of continuity; the intermediate value theorem asserts that the image of an interval by a continuous function is an interval; integrals of real functions are defined over an interval; etc. Interval ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integral
In mathematics, an integral is the continuous analog of a Summation, sum, which is used to calculate area, areas, volume, volumes, and their generalizations. Integration, the process of computing an integral, is one of the two fundamental operations of calculus,Integral calculus is a very well established mathematical discipline for which there are many sources. See and , for example. the other being Derivative, differentiation. Integration was initially used to solve problems in mathematics and physics, such as finding the area under a curve, or determining displacement from velocity. Usage of integration expanded to a wide variety of scientific fields thereafter. A definite integral computes the signed area of the region in the plane that is bounded by the Graph of a function, graph of a given Function (mathematics), function between two points in the real line. Conventionally, areas above the horizontal Coordinate axis, axis of the plane are positive while areas below are n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integration By Parts
In calculus, and more generally in mathematical analysis, integration by parts or partial integration is a process that finds the integral of a product of functions in terms of the integral of the product of their derivative and antiderivative. It is frequently used to transform the antiderivative of a product of functions into an antiderivative for which a solution can be more easily found. The rule can be thought of as an integral version of the product rule of differentiation; it is indeed derived using the product rule. The integration by parts formula states: \begin \int_a^b u(x) v'(x) \, dx & = \Big (x) v(x)\Biga^b - \int_a^b u'(x) v(x) \, dx\\ & = u(b) v(b) - u(a) v(a) - \int_a^b u'(x) v(x) \, dx. \end Or, letting u = u(x) and du = u'(x) \,dx while v = v(x) and dv = v'(x) \, dx, the formula can be written more compactly: \int u \, dv \ =\ uv - \int v \, du. The former expression is written as a definite integral and the latter is written as an indefinite ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Proof
A mathematical proof is a deductive reasoning, deductive Argument-deduction-proof distinctions, argument for a Proposition, mathematical statement, showing that the stated assumptions logically guarantee the conclusion. The argument may use other previously established statements, such as theorems; but every proof can, in principle, be constructed using only certain basic or original assumptions known as axioms, along with the accepted rules of inference. Proofs are examples of exhaustive deductive reasoning that establish logical certainty, to be distinguished from empirical evidence, empirical arguments or non-exhaustive inductive reasoning that establish "reasonable expectation". Presenting many cases in which the statement holds is not enough for a proof, which must demonstrate that the statement is true in ''all'' possible cases. A proposition that has not been proved but is believed to be true is known as a conjecture, or a hypothesis if frequently used as an assumption for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
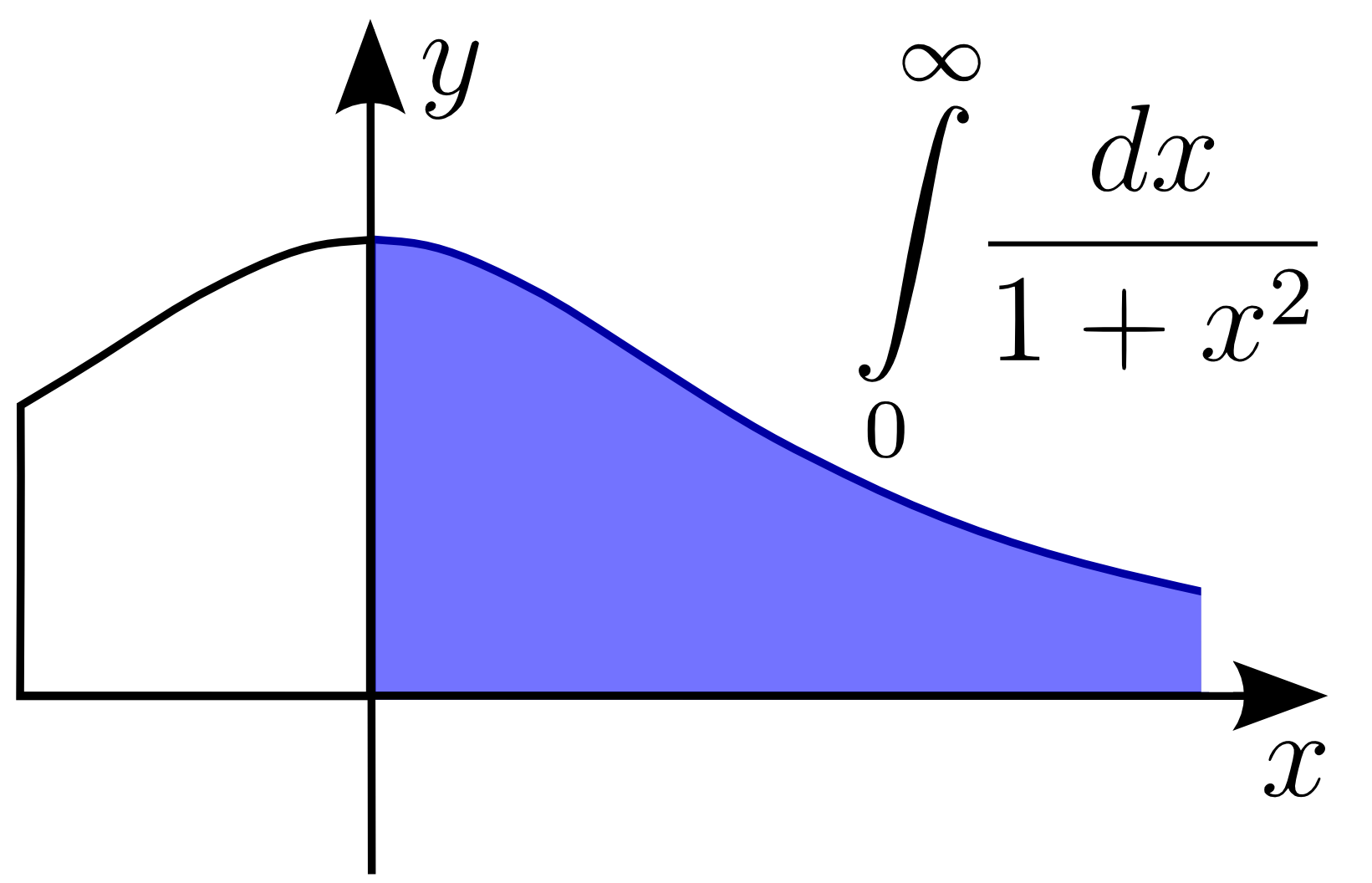
Improper Integral
In mathematical analysis, an improper integral is an extension of the notion of a definite integral to cases that violate the usual assumptions for that kind of integral. In the context of Riemann integrals (or, equivalently, Darboux integrals), this typically involves unboundedness, either of the set over which the integral is taken or of the integrand (the function being integrated), or both. It may also involve bounded but not closed sets or bounded but not continuous functions. While an improper integral is typically written symbolically just like a standard definite integral, it actually represents a limit of a definite integral or a sum of such limits; thus improper integrals are said to converge or diverge. If a regular definite integral (which may retronymically be called a proper integral) is worked out as if it is improper, the same answer will result. In the simplest case of a real-valued function of a single variable integrated in the sense of Riemann (or Darbou ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Corollary
In mathematics and logic, a corollary ( , ) is a theorem of less importance which can be readily deduced from a previous, more notable statement. A corollary could, for instance, be a proposition which is incidentally proved while proving another proposition; it might also be used more casually to refer to something which naturally or incidentally accompanies something else. Overview In mathematics, a corollary is a theorem connected by a short proof to an existing theorem. The use of the term ''corollary'', rather than ''proposition'' or ''theorem'', is intrinsically subjective. More formally, proposition ''B'' is a corollary of proposition ''A'', if ''B'' can be readily deduced from ''A'' or is self-evident from its proof. In many cases, a corollary corresponds to a special case of a larger theorem, which makes the theorem easier to use and apply, even though its importance is generally considered to be secondary to that of the theorem. In particular, ''B'' is unlikely to be te ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Alternating Series Test
In mathematical analysis, the alternating series test proves that an alternating series is convergent when its terms decrease monotonically in absolute value and approach zero in the limit. The test was devised by Gottfried Leibniz and is sometimes known as Leibniz's test, Leibniz's rule, or the Leibniz criterion. The test is only sufficient, not necessary, so some convergent alternating series may fail the first part of the test. For a generalization, see Dirichlet's test. History Leibniz discussed the criterion in his unpublished ''De quadratura arithmetica'' of 1676 and shared his result with Jakob Hermann in June 1705 and with Johann Bernoulli in October, 1713. It was only formally published in 1993. Formal statement Alternating series test A series of the form \sum_^\infty (-1)^ a_n = a_0-a_1 + a_2 - a_3 + \cdots where either all ''a''''n'' are positive or all ''a''''n'' are negative, is called an alternating series. The alternating series test guarantees that ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Direct Comparison Test
In mathematics, the comparison test, sometimes called the direct comparison test to distinguish it from similar related tests (especially the limit comparison test), provides a way of deducing whether an infinite series or an improper integral converges or diverges by comparing the series or integral to one whose convergence properties are known. For series In calculus, the comparison test for series typically consists of a pair of statements about infinite series with non-negative ( real-valued) terms: * If the infinite series \sum b_n converges and 0 \le a_n \le b_n for all sufficiently large ''n'' (that is, for all n>N for some fixed value ''N''), then the infinite series \sum a_n also converges. * If the infinite series \sum b_n diverges and 0 \le b_n \le a_n for all sufficiently large ''n'', then the infinite series \sum a_n also diverges. Note that the series having larger terms is sometimes said to ''dominate'' (or ''eventually dominate'') the series with smaller terms. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bounded Function
In mathematics, a function f defined on some set X with real or complex values is called bounded if the set of its values (its image) is bounded. In other words, there exists a real number M such that :, f(x), \le M for all x in X. A function that is ''not'' bounded is said to be unbounded. If f is real-valued and f(x) \leq A for all x in X, then the function is said to be bounded (from) above by A. If f(x) \geq B for all x in X, then the function is said to be bounded (from) below by B. A real-valued function is bounded if and only if it is bounded from above and below. An important special case is a bounded sequence, where ''X'' is taken to be the set \mathbb N of natural numbers. Thus a sequence f = (a_0, a_1, a_2, \ldots) is bounded if there exists a real number M such that :, a_n, \le M for every natural number n. The set of all bounded sequences forms the sequence space l^\infty. The definition of boundedness can be generalized to functions f: X \rightarrow Y taking ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convergent Series
In mathematics, a series is the sum of the terms of an infinite sequence of numbers. More precisely, an infinite sequence (a_1, a_2, a_3, \ldots) defines a series that is denoted :S=a_1 + a_2 + a_3 + \cdots=\sum_^\infty a_k. The th partial sum is the sum of the first terms of the sequence; that is, :S_n = a_1 +a_2 + \cdots + a_n = \sum_^n a_k. A series is convergent (or converges) if and only if the sequence (S_1, S_2, S_3, \dots) of its partial sums tends to a limit; that means that, when adding one a_k after the other ''in the order given by the indices'', one gets partial sums that become closer and closer to a given number. More precisely, a series converges, if and only if there exists a number \ell such that for every arbitrarily small positive number \varepsilon, there is a (sufficiently large) integer N such that for all n \ge N, :\left , S_n - \ell \right , 1 produce a convergent series: *: ++++++\cdots = . * Alternating the signs of reciprocals of powers o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |