|
Circular Sector
A circular sector, also known as circle sector or disk sector or simply a sector (symbol: ⌔), is the portion of a disk (a closed region bounded by a circle) enclosed by two radii and an arc, with the smaller area being known as the ''minor sector'' and the larger being the ''major sector''. In the diagram, is the central angle, the radius of the circle, and is the arc length of the minor sector. The angle formed by connecting the endpoints of the arc to any point on the circumference that is not in the sector is equal to half the central angle. Types A sector with the central angle of 180° is called a '' half-disk'' and is bounded by a diameter and a semicircle. Sectors with other central angles are sometimes given special names, such as quadrants (90°), sextants (60°), and octants (45°), which come from the sector being one quarter, sixth or eighth part of a full circle, respectively. Area The total area of a circle is . The area of the sector can be obtai ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Circle Arc
A circle is a shape consisting of all points in a plane that are at a given distance from a given point, the centre. The distance between any point of the circle and the centre is called the radius. The length of a line segment connecting two points on the circle and passing through the centre is called the diameter. A circle bounds a region of the plane called a disc. The circle has been known since before the beginning of recorded history. Natural circles are common, such as the full moon or a slice of round fruit. The circle is the basis for the wheel, which, with related inventions such as gears, makes much of modern machinery possible. In mathematics, the study of the circle has helped inspire the development of geometry, astronomy and calculus. Terminology * Annulus: a ring-shaped object, the region bounded by two concentric circles. * Arc: any connected part of a circle. Specifying two end points of an arc and a centre allows for two arcs that together make u ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Perimeter
A perimeter is the length of a closed boundary that encompasses, surrounds, or outlines either a two-dimensional shape or a one-dimensional line. The perimeter of a circle or an ellipse is called its circumference. Calculating the perimeter has several practical applications. A calculated perimeter is the length of fence required to surround a yard or garden. The perimeter of a wheel/circle (its circumference) describes how far it will roll in one revolution. Similarly, the amount of string wound around a spool is related to the spool's perimeter; if the length of the string was exact, it would equal the perimeter. Formulas The perimeter is the distance around a shape. Perimeters for more general shapes can be calculated, as any path, with \int_0^L \mathrms, where L is the length of the path and ds is an infinitesimal line element. Both of these must be replaced by algebraic forms in order to be practically calculated. If the perimeter is given as a closed piecewise ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Longman
Longman, also known as Pearson Longman, is a publisher, publishing company founded in 1724 in London, England, which is owned by Pearson PLC. Since 1968, Longman has been used primarily as an imprint by Pearson's Schools business. The Longman brand is also used for the Longman Schools in China and the ''Longman Dictionary of Contemporary English, Longman Dictionary''. History Beginnings The Longman company was founded by Thomas Longman (1699–1755), Thomas Longman (1699 – 18 June 1755), the son of Ezekiel Longman (died 1708), a gentleman of Bristol. Thomas was apprenticed in 1716 to John Osborn, a London bookseller, and at the expiration of his apprenticeship married Osborn's daughter. In August 1724, he purchased the stock and household goods of William Taylor (bookseller), William Taylor, the first publisher of ''Robinson Crusoe'', for 9s 6d. Taylor's two shops in Paternoster Row, London, were known respectively as the ''Black Swan (St. Paul's Churchyard), Bl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
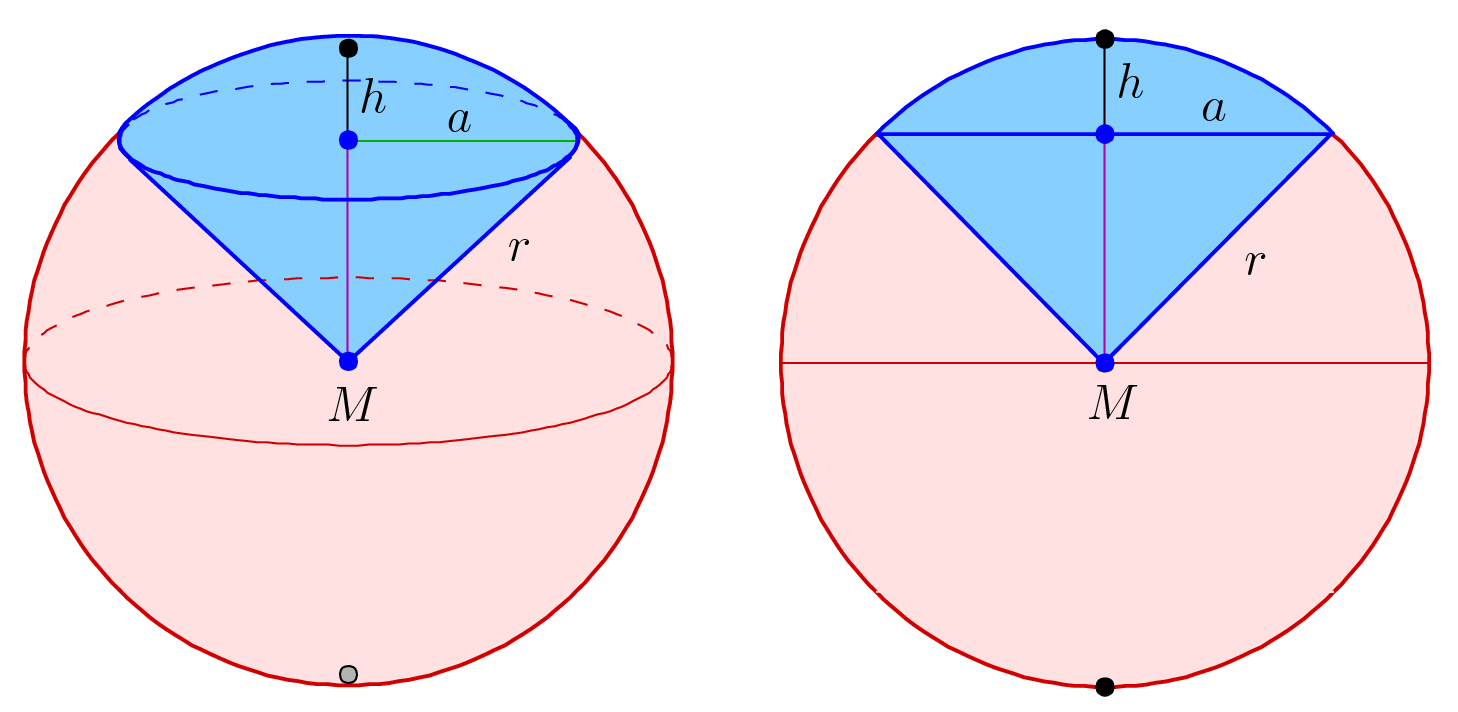
Spherical Sector
In geometry, a spherical sector, also known as a spherical cone, is a portion of a sphere or of a ball defined by a conical boundary with apex at the center of the sphere. It can be described as the union of a spherical cap and the cone formed by the center of the sphere and the base of the cap. It is the three-dimensional analogue of the sector of a circle. Volume If the radius of the sphere is denoted by and the height of the cap by , the volume of the spherical sector is V = \frac\,. This may also be written as V = \frac (1-\cos\varphi)\,, where is half the cone aperture angle, i.e., is the angle between the rim of the cap and the axis direction to the middle of the cap as seen from the sphere center. The limiting case is for approaching 180 degrees, which then describes a complete sphere. The height, is given by h = r (1-\cos\varphi)\,. The volume of the sector is related to the area of the cap by: V = \frac\,. Area The curved surface area of the spherical se ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Sector Of (mathematics)
is a mathematical notation defined by , where is the cosine function, is the imaginary unit and is the sine function. is the argument of the complex number (angle between line to point and x-axis in polar form). The notation is less commonly used in mathematics than Euler's formula, which offers an even shorter notation for but cis(x) is widely used as a name for this function in software libraries. Overview The notation is a shorthand for the combination of functions on the right-hand side of Euler's formula: : e^ = \cos x + i\sin x, where . So, : \operatorname x = \cos x + i\sin x, i.e. "" is an acronym for "". It connects trigonometric functions with exponential functions in the complex plane via Euler's formula. While the domain of definition is usually x \in \mathbb, complex values z \in \mathbb are possible as well: : \operatorname z = \cos z + i\sin z, so the function can be used to extend Euler's formula to a more general complex version. The function is m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Hyperbolic Sector
A hyperbolic sector is a region (mathematics), region of the Cartesian plane bounded by a hyperbola and two ray (geometry), rays from the origin to it. For example, the two points and on the Hyperbola#Rectangular hyperbola, rectangular hyperbola , or the corresponding region when this hyperbola is re-scaled and its orientation (geometry), orientation is altered by a Rotation (geometry), rotation leaving the center at the origin, as with the Unit hyperbola#Parametrization, unit hyperbola. A hyperbolic sector in standard position has and . The argument of hyperbolic functions is the hyperbolic angle, which is defined as the area of a hyperbolic sector of the standard hyperbola ''xy'' = 1. This area is evaluated using natural logarithm. Hyperbolic triangle When in standard position, a hyperbolic sector determines a hyperbolic triangle, the right triangle with one vertex (geometry), vertex at the origin, base on the diagonal ray ''y'' = ''x'', and third vertex on the h ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Earth Quadrant
In geodesy and navigation, a meridian arc is the curve between two points near the Earth's surface having the same longitude. The term may refer either to a segment of the meridian, or to its length. Both the practical determination of meridian arcs (employing measuring instruments in field campaigns) as well as its theoretical calculation (based on geometry and abstract mathematics) have been pursued for many years. Measurement The purpose of measuring meridian arcs is to determine a figure of the Earth. One or more measurements of meridian arcs can be used to infer the shape of the reference ellipsoid that best approximates the geoid in the region of the measurements. Measurements of meridian arcs at several latitudes along many meridians around the world can be combined in order to approximate a ''geocentric ellipsoid'' intended to fit the entire world. The earliest determinations of the size of a spherical Earth required a single arc. Accurate survey work beginning in th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Conic Section
A conic section, conic or a quadratic curve is a curve obtained from a cone's surface intersecting a plane. The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is a special case of the ellipse, though it was sometimes considered a fourth type. The ancient Greek mathematicians studied conic sections, culminating around 200 BC with Apollonius of Perga's systematic work on their properties. The conic sections in the Euclidean plane have various distinguishing properties, many of which can be used as alternative definitions. One such property defines a non-circular conic to be the set of those points whose distances to some particular point, called a '' focus'', and some particular line, called a ''directrix'', are in a fixed ratio, called the ''eccentricity''. The type of conic is determined by the value of the eccentricity. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2; that is, as the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Circular Segment
In geometry, a circular segment or disk segment (symbol: ) is a region of a disk which is "cut off" from the rest of the disk by a straight line. The complete line is known as a '' secant'', and the section inside the disk as a '' chord''. More formally, a circular segment is a plane region bounded by a circular arc (of less than π radians by convention) and the circular chord connecting its endpoints. Formulae Let ''R'' be the radius of the arc which forms part of the perimeter of the segment, ''θ'' the central angle subtending the arc in radians, ''c'' the chord length, ''s'' the arc length, ''h'' the sagitta (height) of the segment, ''d'' the apothem of the segment, and ''a'' the area of the segment. Usually, chord length and height are given or measured, and sometimes the arc length as part of the perimeter, and the unknowns are area and sometimes arc length. These can't be calculated simply from chord length and height, so two intermediate quantities, the radius ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Chord (geometry)
A chord (from the Latin ''chorda'', meaning " bowstring") of a circle is a straight line segment whose endpoints both lie on a circular arc. If a chord were to be extended infinitely on both directions into a line, the object is a ''secant line''. The perpendicular line passing through the chord's midpoint is called '' sagitta'' (Latin for "arrow"). More generally, a chord is a line segment joining two points on any curve, for instance, on an ellipse. A chord that passes through a circle's center point is the circle's ''diameter''. In circles Among properties of chords of a circle are the following: # Chords are equidistant from the center if and only if their lengths are equal. # Equal chords are subtended by equal angles from the center of the circle. # A chord that passes through the center of a circle is called a diameter and is the longest chord of that specific circle. # If the line extensions (secant lines) of chords AB and CD intersect at a point P, then their ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
West Conshohocken, Pennsylvania
West Conshohocken is a Borough (Pennsylvania), borough in Montgomery County, Pennsylvania, Montgomery County, Pennsylvania, United States. The population was 1,320 at the 2010 census. Its sister community is Conshohocken, Pennsylvania, Conshohocken, located across the Schuylkill River. Montgomery County's seat, Norristown, Pennsylvania, Norristown, is located approximately two miles north of, and on the opposite side of the river from, West Conshohocken. History West Conshohocken was incorporated October 6, 1874, from land taken almost equally from Lower and Upper Merion Townships. The area's original name had been ''Balligomingo.'' As a river borough, there were a large number of mills and other industries utilizing water power. Dougherty Quarry was a prosperous business, producing stone of superior quality known as ''Conshohocken'' or ''Merion Blue''. It was much sought after for public buildings, and was shipped by rail throughout the East Coast of the United States, East Co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Cengage
Cengage Group is an American educational content, technology, and services company for higher education, K–12, professional, and library markets. It operates in more than 20 countries around the world.(June 27, 2014Global Publishing Leaders 2014: Cengage publishersweekly.comCompany Info – Wall Street JournalCengage LearningCompany Overview of Cengage Learning, Inc. BloombergBusiness Company information The company is headquartered in , Massachusetts, and has some 5,000 employees worldwide across nearly 38 countries. It was headquartered at its |