|
Chapman–Kolmogorov Equation
In mathematics, specifically in the theory of Markovian stochastic processes in probability theory, the Chapman–Kolmogorov equation (CKE) is an identity relating the joint probability distributions of different sets of coordinates on a stochastic process. The equation was derived independently by both the British mathematician Sydney Chapman and the Russian mathematician Andrey Kolmogorov. The CKE is prominently used in recent variational Bayesian methods. Mathematical description Suppose that is an indexed collection of random variables, that is, a stochastic process. Let :p_(f_1,\ldots,f_n) be the joint probability density function of the values of the random variables ''f''1 to ''fn''. Then, the Chapman–Kolmogorov equation is :p_(f_1,\ldots,f_)=\int_^p_(f_1,\ldots,f_n)\,df_n i.e. a straightforward marginalization over the nuisance variable. (Note that nothing yet has been assumed about the temporal (or any other) ordering of the random variables—the above equatio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Category Of Markov Kernels
In mathematics, the category of Markov kernels, often denoted Stoch, is the category whose objects are measurable spaces and whose morphisms are Markov kernels. It is analogous to the category of sets and functions, but where the arrows can be interpreted as being stochastic. Several variants of this category are used in the literature. For example, one can use subprobability kernels instead of probability kernels, or more general s-finite kernels. Also, one can take as morphisms equivalence classes of Markov kernels under almost sure equality; see below. Definition Recall that a Markov kernel between measurable spaces (X,\mathcal) and (Y,\mathcal) is an assignment k:X\times\mathcal\to\mathbb which is measurable as a function on X and which is a probability measure on \mathcal. We denote its values by k(B, x) for x\in X and B\in\mathcal, which suggests an interpretation as conditional probability. The category Stoch has: * As objects, measurable spaces; * As morphisms, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Equations
In mathematics, an equation is a mathematical formula that expresses the equality of two expressions, by connecting them with the equals sign . The word ''equation'' and its cognates in other languages may have subtly different meanings; for example, in French an ''équation'' is defined as containing one or more variables, while in English, any well-formed formula consisting of two expressions related with an equals sign is an equation. Solving an equation containing variables consists of determining which values of the variables make the equality true. The variables for which the equation has to be solved are also called unknowns, and the values of the unknowns that satisfy the equality are called solutions of the equation. There are two kinds of equations: identities and conditional equations. An identity is true for all values of the variables. A conditional equation is only true for particular values of the variables. The " =" symbol, which appears in every equation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Category Of Markov Kernels
In mathematics, the category of Markov kernels, often denoted Stoch, is the category whose objects are measurable spaces and whose morphisms are Markov kernels. It is analogous to the category of sets and functions, but where the arrows can be interpreted as being stochastic. Several variants of this category are used in the literature. For example, one can use subprobability kernels instead of probability kernels, or more general s-finite kernels. Also, one can take as morphisms equivalence classes of Markov kernels under almost sure equality; see below. Definition Recall that a Markov kernel between measurable spaces (X,\mathcal) and (Y,\mathcal) is an assignment k:X\times\mathcal\to\mathbb which is measurable as a function on X and which is a probability measure on \mathcal. We denote its values by k(B, x) for x\in X and B\in\mathcal, which suggests an interpretation as conditional probability. The category Stoch has: * As objects, measurable spaces; * As morphisms, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Examples Of Markov Chains
Example may refer to: * ''exempli gratia'' (e.g.), usually read out in English as "for example" * .example, reserved as a domain name that may not be installed as a top-level domain of the Internet ** example.com, example.net, example.org, and example.edu: second-level domain names reserved for use in documentation as examples * HMS ''Example'' (P165), an Archer-class patrol and training vessel of the Royal Navy Arts * ''The Example'', a 1634 play by James Shirley * ''The Example'' (comics), a 2009 graphic novel by Tom Taylor and Colin Wilson * Example (musician), the British dance musician Elliot John Gleave (born 1982) * ''Example'' (album), a 1995 album by American rock band For Squirrels See also * Exemplar (other), a prototype or model which others can use to understand a topic better * Exemplum An exemplum (Latin for "example", exempla, ''exempli gratia'' = "for example", abbr.: ''e.g.'') is a moral anecdote, brief or extended, real or fictitious, us ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Kolmogorov Backward Equation
In probability theory, Kolmogorov equations characterize continuous-time Markov processes. In particular, they describe how the probability of a continuous-time Markov process in a certain state changes over time. There are four distinct equations: the Kolmogorov forward equation for continuous processes, now understood to be identical to the Fokker–Planck equation, the Kolmogorov forward equation for jump processes, and two Kolmogorov backward equations for processes with and without discontinuous jumps. Diffusion processes vs. jump processes Writing in 1931, Andrei Kolmogorov started from the theory of discrete time Markov processes, which are described by the Chapman–Kolmogorov equation, and sought to derive a theory of continuous time Markov processes by extending this equation. He found that there are two kinds of continuous time Markov processes, depending on the assumed behavior over small intervals of time: If you assume that "in a small time interval there i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
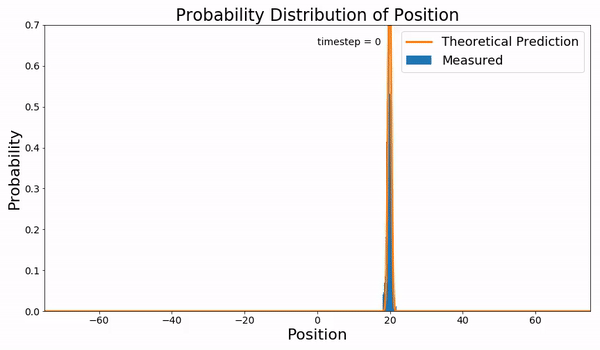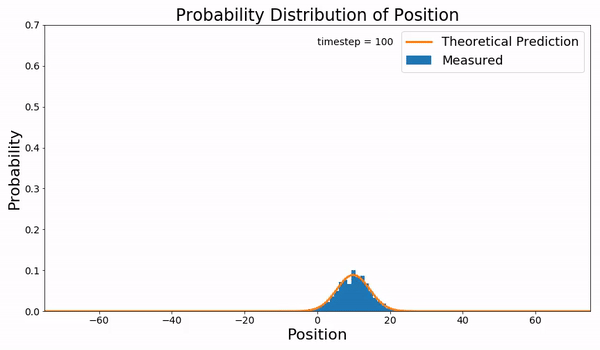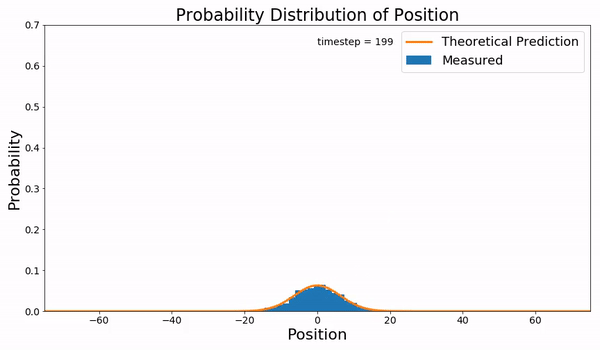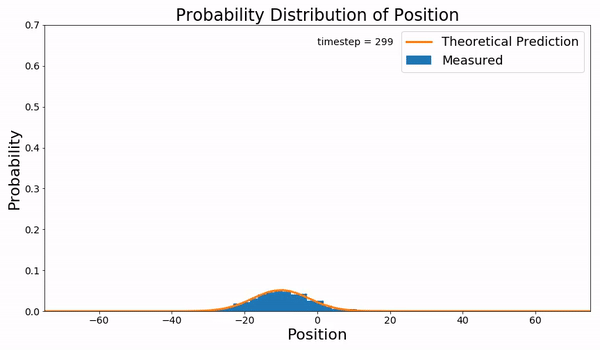 |
Fokker–Planck Equation
In statistical mechanics and information theory, the Fokker–Planck equation is a partial differential equation that describes the time evolution of the probability density function of the velocity of a particle under the influence of drag (physics), drag forces and random forces, as in Brownian motion. The equation can be generalized to other observables as well. The Fokker–Planck equation has multiple applications in information theory, graph theory, data science, finance, economics etc. It is named after Adriaan Fokker and Max Planck, who described it in 1914 and 1917. It is also known as the Kolmogorov forward equation, after Andrey Kolmogorov, who independently discovered it in 1931. When applied to particle position distributions, it is better known as the Smoluchowski equation (after Marian Smoluchowski), and in this context it is equivalent to the convection–diffusion equation. When applied to particle position and momentum distributions, it is known as the Klein–Kr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Master Equation
In physics, chemistry, and related fields, master equations are used to describe the time evolution of a system that can be modeled as being in a probabilistic combination of states at any given time, and the switching between states is determined by a transition rate matrix. The equations are a set of differential equations – over time – of the probabilities that the system occupies each of the different states. The name was proposed in 1940: Introduction A master equation is a phenomenological set of first-order differential equations describing the time evolution of (usually) the probability of a system to occupy each one of a discrete set of states with regard to a continuous time variable ''t''. The most familiar form of a master equation is a matrix form: \frac = \mathbf\vec, where \vec is a column vector, and \mathbf is the matrix of connections. The way connections among states are made determines the dimension of the problem; it is either *a d-dimension ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Matrix Multiplication
In mathematics, specifically in linear algebra, matrix multiplication is a binary operation that produces a matrix (mathematics), matrix from two matrices. For matrix multiplication, the number of columns in the first matrix must be equal to the number of rows in the second matrix. The resulting matrix, known as the matrix product, has the number of rows of the first and the number of columns of the second matrix. The product of matrices and is denoted as . Matrix multiplication was first described by the French mathematician Jacques Philippe Marie Binet in 1812, to represent the composition of functions, composition of linear maps that are represented by matrices. Matrix multiplication is thus a basic tool of linear algebra, and as such has numerous applications in many areas of mathematics, as well as in applied mathematics, statistics, physics, economics, and engineering. Computing matrix products is a central operation in all computational applications of linear algebra. Not ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Probability Distribution
In probability theory and statistics, a probability distribution is a Function (mathematics), function that gives the probabilities of occurrence of possible events for an Experiment (probability theory), experiment. It is a mathematical description of a Randomness, random phenomenon in terms of its sample space and the Probability, probabilities of Event (probability theory), events (subsets of the sample space). For instance, if is used to denote the outcome of a coin toss ("the experiment"), then the probability distribution of would take the value 0.5 (1 in 2 or 1/2) for , and 0.5 for (assuming that fair coin, the coin is fair). More commonly, probability distributions are used to compare the relative occurrence of many different random values. Probability distributions can be defined in different ways and for discrete or for continuous variables. Distributions with special properties or for especially important applications are given specific names. Introduction A prob ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Transition Probability
In probability theory and statistics, a Markov chain or Markov process is a stochastic process describing a sequence of possible events in which the probability of each event depends only on the state attained in the previous event. Informally, this may be thought of as, "What happens next depends only on the state of affairs ''now''." A countably infinite sequence, in which the chain moves state at discrete time steps, gives a discrete-time Markov chain (DTMC). A continuous-time process is called a continuous-time Markov chain (CTMC). Markov processes are named in honor of the Russian mathematician Andrey Markov. Markov chains have many applications as statistical models of real-world processes. They provide the basis for general stochastic simulation methods known as Markov chain Monte Carlo, which are used for simulating sampling from complex probability distributions, and have found application in areas including Bayesian statistics, biology, chemistry, economics, finance, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Markov Property
In probability theory and statistics, the term Markov property refers to the memoryless property of a stochastic process, which means that its future evolution is independent of its history. It is named after the Russian mathematician Andrey Markov. The term strong Markov property is similar to the Markov property, except that the meaning of "present" is defined in terms of a random variable known as a stopping time. The term Markov assumption is used to describe a model where the Markov property is assumed to hold, such as a hidden Markov model. A Markov random field extends this property to two or more dimensions or to random variables defined for an interconnected network of items. An example of a model for such a field is the Ising model. A discrete-time stochastic process satisfying the Markov property is known as a Markov chain. Introduction A stochastic process has the Markov property if the conditional probability distribution of future states of the process (cond ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |