|
Vigesimal Numeral Systems
A vigesimal ( ) or base-20 (base-score) numeral system is based on twenty (in the same way in which the decimal numeral system is based on ten). ''Vigesimal'' is derived from the Latin adjective , meaning 'twentieth'. Places In a vigesimal place system, twenty individual numerals (or digit symbols) are used, ten more than in the decimal system. One modern method of finding the extra needed symbols is to write ten as the letter A, or , where the 20 means base , to write nineteen as , and the numbers between with the corresponding letters of the alphabet. This is similar to the common computer-science practice of writing hexadecimal numerals over 9 with the letters "A–F". Another less common method skips over the letter "I", in order to avoid confusion between I20 as eighteen and one, so that the number eighteen is written as J20, and nineteen is written as K20. The number twenty is written as . According to this notation: : is equivalent to forty in decimal = : is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Maya
Maya may refer to: Ethnic groups * Maya peoples, of southern Mexico and northern Central America ** Maya civilization, the historical civilization of the Maya peoples ** Mayan languages, the languages of the Maya peoples * Maya (East Africa), a population native to the old Wej province in Ethiopia * Sibuyanon, a Visayan population sometimes "May-" native to Sibuyan Island in the Philippines Religion and mythology * Maya (religion), in Indian religions, relates to the illusion of reality * Maya (mother of the Buddha) (died 563 BC), mother of the historical Buddha * Mayasura or Maya, a Hindu demon * Maya religion The traditional Maya or Mayan religion of the extant Maya peoples of Guatemala, Belize, western Honduras, and the Tabasco, Chiapas, Quintana Roo, Campeche and Yucatán states of Mexico is part of the wider frame of Mesoamerican religion. As ..., the religious practices of the Maya peoples of parts of Mexico and Central America ** Maya mythology, the myths and leg ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
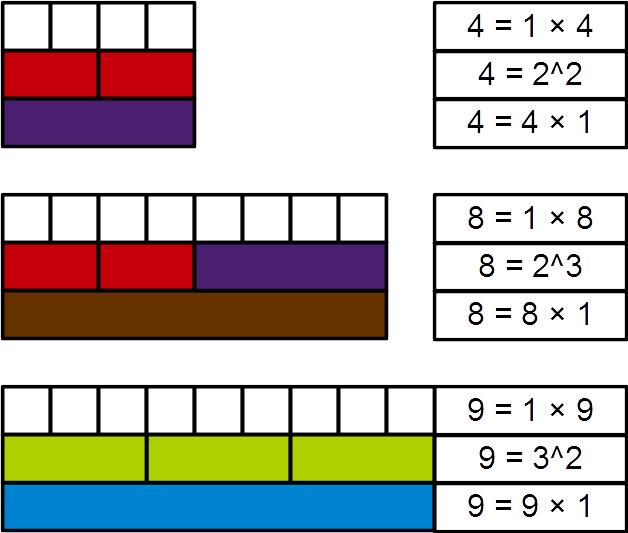
Perfect Power
In mathematics, a perfect power is a natural number that is a product of equal natural factors, or, in other words, an integer that can be expressed as a square or a higher integer power of another integer greater than one. More formally, ''n'' is a perfect power if there exist natural numbers ''m'' > 1, and ''k'' > 1 such that ''mk'' = ''n''. In this case, ''n'' may be called a perfect ''k''th power. If ''k'' = 2 or ''k'' = 3, then ''n'' is called a perfect square or perfect cube, respectively. Sometimes 0 and 1 are also considered perfect powers (0''k'' = 0 for any ''k'' > 0, 1''k'' = 1 for any ''k''). Examples and sums A sequence of perfect powers can be generated by iterating through the possible values for ''m'' and ''k''. The first few ascending perfect powers in numerical order (showing duplicate powers) are : : 2^2 = 4,\ 2^3 = 8,\ 3^2 = 9,\ 2^4 = 16,\ 4^2 = 16,\ 5^2 = 25,\ 3^3 = 27, 2^5 = 32,\ 6^2 = 36,\ 7^2 = 49,\ 2^6 = 64,\ 4^3 = 64,\ 8^2 = 64, \dots The sum o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diameter
In geometry, a diameter of a circle is any straight line segment that passes through the centre of the circle and whose endpoints lie on the circle. It can also be defined as the longest Chord (geometry), chord of the circle. Both definitions are also valid for the diameter of a sphere. In more modern usage, the length d of a diameter is also called the diameter. In this sense one speaks of diameter rather than diameter (which refers to the line segment itself), because all diameters of a circle or sphere have the same length, this being twice the radius r. :d = 2r \qquad\text\qquad r = \frac. The word "diameter" is derived from (), "diameter of a circle", from (), "across, through" and (), "measure". It is often abbreviated \text, \text, d, or \varnothing. Constructions With straightedge and compass, a diameter of a given circle can be constructed as the perpendicular bisector of an arbitrary chord. Drawing two diameters in this way can be used to locate the center of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Circumference
In geometry, the circumference () is the perimeter of a circle or ellipse. The circumference is the arc length of the circle, as if it were opened up and straightened out to a line segment. More generally, the perimeter is the curve length around any closed figure. Circumference may also refer to the circle itself, that is, the Locus (geometry), locus corresponding to the Edge (geometry), edge of a Disk (geometry), disk. The is the circumference, or length, of any one of its great circles. Circle The circumference of a circle is the distance around it, but if, as in many elementary treatments, distance is defined in terms of straight lines, this cannot be used as a definition. Under these circumstances, the circumference of a circle may be defined as the Limit (mathematics), limit of the perimeters of inscribed regular polygons as the number of sides increases without bound. The term circumference is used when measuring physical objects, as well as when considering abstrac ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Golden Ratio
In mathematics, two quantities are in the golden ratio if their ratio is the same as the ratio of their summation, sum to the larger of the two quantities. Expressed algebraically, for quantities and with , is in a golden ratio to if \frac = \frac = \varphi, where the Greek letter Phi (letter), phi ( or ) denotes the golden ratio. The constant satisfies the quadratic equation and is an irrational number with a value of The golden ratio was called the extreme and mean ratio by Euclid, and the divine proportion by Luca Pacioli; it also goes by other names. Mathematicians have studied the golden ratio's properties since antiquity. It is the ratio of a regular pentagon's diagonal to its side and thus appears in the Straightedge and compass construction, construction of the dodecahedron and icosahedron. A golden rectangle—that is, a rectangle with an aspect ratio of —may be cut into a square and a smaller rectangle with the same aspect ratio. The golden ratio has bee ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rectangle
In Euclidean geometry, Euclidean plane geometry, a rectangle is a Rectilinear polygon, rectilinear convex polygon or a quadrilateral with four right angles. It can also be defined as: an equiangular quadrilateral, since equiangular means that all of its angles are equal (360°/4 = 90°); or a parallelogram containing a right angle. A rectangle with four sides of equal length is a ''square''. The term "wikt:oblong, oblong" is used to refer to a non-square rectangle. A rectangle with Vertex (geometry), vertices ''ABCD'' would be denoted as . The word rectangle comes from the Latin ''rectangulus'', which is a combination of ''rectus'' (as an adjective, right, proper) and ''angulus'' (angle). A #Crossed rectangles, crossed rectangle is a crossed (self-intersecting) quadrilateral which consists of two opposite sides of a rectangle along with the two diagonals (therefore only two sides are parallel). It is a special case of an antiparallelogram, and its angles are not right angles an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Square Root Of 5
The square root of 5 is the positive real number that, when multiplied by itself, gives the prime number 5. It is more precisely called the principal square root of 5, to distinguish it from the negative number with the same property. This number appears in the fractional expression for the golden ratio. It can be denoted in surd form as \sqrt. It is an irrational algebraic number. The first sixty significant digits of its decimal expansion are: : , which can be rounded down to 2.236 to within 99.99% accuracy. The approximation (≈ 2.23611) for the square root of five can be used. Despite having a denominator of only 72, it differs from the correct value by less than (approx. ). As of January 2022, the numerical value in decimal of the square root of 5 has been computed to at least 2,250,000,000,000 digits. Rational approximations The square root of 5 can be expressed as the simple continued fraction : ; 4, 4, 4, 4, 4,\ldots= 2 + \cfrac 1 . The successive partial eva ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cube
A cube or regular hexahedron is a three-dimensional space, three-dimensional solid object in geometry, which is bounded by six congruent square (geometry), square faces, a type of polyhedron. It has twelve congruent edges and eight vertices. It is a type of parallelepiped, with pairs of parallel opposite faces, and more specifically a rhombohedron, with congruent edges, and a rectangular cuboid, with right angles between pairs of intersecting faces and pairs of intersecting edges. It is an example of many classes of polyhedra: Platonic solid, regular polyhedron, parallelohedron, zonohedron, and plesiohedron. The dual polyhedron of a cube is the regular octahedron. The cube can be represented in many ways, one of which is the graph known as the cubical graph. It can be constructed by using the Cartesian product of graphs. The cube is the three-dimensional hypercube, a family of polytopes also including the two-dimensional square and four-dimensional tesseract. A cube with 1, unit s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Square Root Of 3
The square root of 3 is the positive real number that, when multiplied by itself, gives the number 3. It is denoted mathematically as \sqrt or 3^. It is more precisely called the principal square root of 3 to distinguish it from the negative number with the same property. The square root of 3 is an irrational number. It is also known as Theodorus' constant, after Theodorus of Cyrene, who proved its irrationality. In 2013, its numerical value in decimal notation was computed to ten billion digits. Its decimal expansion, written here to 65 decimal places, is given by : : The fraction \frac (...) can be used as a good approximation. Despite having a denominator of only 56, it differs from the correct value by less than \frac (approximately 9.2\times 10^, with a relative error of 5\times 10^). The rounded value of is correct to within 0.01% of the actual value. The fraction \frac (...) is accurate to 1\times 10^. Archimedes reported a range for its value: (\frac)^>3>(\frac)^ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Square (geometry)
In geometry, a square is a regular quadrilateral. It has four straight sides of equal length and four equal angles. Squares are special cases of rectangles, which have four equal angles, and of rhombuses, which have four equal sides. As with all rectangles, a square's angles are right angles (90 degrees, or /2 radians), making adjacent sides perpendicular. The area of a square is the side length multiplied by itself, and so in algebra, multiplying a number by itself is called squaring. Equal squares can tile the plane edge-to-edge in the square tiling. Square tilings are ubiquitous in tiled floors and walls, graph paper, image pixels, and game boards. Square shapes are also often seen in building floor plans, origami paper, food servings, in graphic design and heraldry, and in instant photos and fine art. The formula for the area of a square forms the basis of the calculation of area and motivates the search for methods for squaring the circle by compass and straightedge ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diagonal
In geometry, a diagonal is a line segment joining two vertices of a polygon or polyhedron, when those vertices are not on the same edge. Informally, any sloping line is called diagonal. The word ''diagonal'' derives from the ancient Greek διαγώνιος ''diagonios'', "from corner to corner" (from διά- ''dia-'', "through", "across" and γωνία ''gonia'', "corner", related to ''gony'' "knee"); it was used by both Strabo and Euclid to refer to a line connecting two vertices of a rhombus or cuboid, and later adopted into Latin as ''diagonus'' ("slanting line"). Polygons As applied to a polygon, a diagonal is a line segment joining any two non-consecutive vertices. Therefore, a quadrilateral has two diagonals, joining opposite pairs of vertices. For any convex polygon, all the diagonals are inside the polygon, but for re-entrant polygons, some diagonals are outside of the polygon. Any ''n''-sided polygon (''n'' ≥ 3), convex or concave, has \tfrac ''total'' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |