|
Tropical Analysis
In the mathematical discipline of idempotent analysis, tropical analysis is the study of the tropical semiring. Applications The max tropical semiring can be used appropriately to determine marking times within a given Petri net and a vector filled with marking state at the beginning: -\infty (unit for max, tropical addition) means "never before", while 0 (unit for addition, tropical multiplication) is "no additional time". Tropical cryptography is cryptography based on the tropical semiring. Tropical geometry is an analog to algebraic geometry, using the tropical semiring. References * Further reading * * See also *Lunar arithmetic Lunar most commonly means "of or relating to the Moon The Moon is Earth's only natural satellite. It Orbit of the Moon, orbits around Earth at Lunar distance, an average distance of (; about 30 times Earth diameter, Earth's diameter). Th ... External links MaxPlus algebraworking group, INRIA Rocquencourt {{Mathanalysi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Idempotent Analysis
In mathematical analysis, idempotent analysis is the study of idempotent semirings, such as the tropical semiring. The lack of an additive inverse in the semiring is compensated somewhat by the idempotent rule A \oplus A = A. References * {{mathanalysis-stub Idempotent analysis, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tropical Semiring
In idempotent analysis, the tropical semiring is a semiring of extended real numbers with the operations of minimum (or maximum) and addition replacing the usual ("classical") operations of addition and multiplication, respectively. The tropical semiring has various applications (see tropical analysis), and forms the basis of tropical geometry. The name ''tropical'' is a reference to the Hungarian-born computer scientist Imre Simon, so named because he lived and worked in Brazil. Definition The ' (or or ) is the semiring (\mathbb \cup \, \oplus, \otimes), with the operations: : x \oplus y = \min\, : x \otimes y = x + y. The operations \oplus and \otimes are referred to as ''tropical addition'' and ''tropical multiplication'' respectively. The identity element for \oplus is +\infty, and the identity element for \otimes is 0. Similarly, the ' (or or or ) is the semiring (\mathbb \cup \, \oplus, \otimes), with operations: : x \oplus y = \max\, : x \otimes y = x + y. The identi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
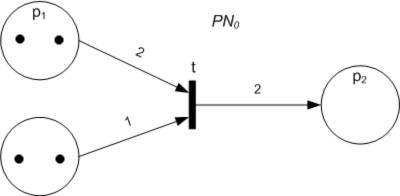
Petri Net
A Petri net, also known as a place/transition net (PT net), is one of several mathematical modeling languages for the description of distributed systems. It is a class of discrete event dynamic system. A Petri net is a directed bipartite graph that has two types of elements: places and transitions. Place elements are depicted as white circles and transition elements are depicted as rectangles. A place can contain any number of tokens, depicted as black circles. A transition is enabled if all places connected to it as inputs contain at least one token. Some sources state that Petri nets were invented in August 1939 by Carl Adam Petri — at the age of 13 — for the purpose of describing chemical processes. Like industry standards such as UML activity diagrams, Business Process Model and Notation, and event-driven process chains, Petri nets offer a graphical notation for stepwise processes that include choice, iteration, and concurrent execution. Unlike these standards, Pet ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tropical Cryptography
In tropical analysis, tropical cryptography refers to the study of a class of cryptographic protocols built upon tropical algebras. In many cases, tropical cryptographic schemes have arisen from adapting classical (non-tropical) schemes to instead rely on tropical algebras. The case for the use of tropical algebras in cryptography rests on at least two key features of tropical mathematics: in the tropical world, there is no classical multiplication (a computationally expensive operation), and the problem of solving systems of tropical polynomial equations has been shown to be NP-hard. Basic Definitions The key mathematical object at the heart of tropical cryptography is the tropical semiring (\mathbb \cup \,\oplus,\otimes) (also known as the min-plus algebra), or a generalization thereof. The operations are defined as follows for x,y \in \mathbb \cup \: x \oplus y = \min\ x \otimes y = x + y It is easily verified that with \infty as the additive identity, these binary operati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tropical Geometry
In mathematics, tropical geometry is the study of polynomials and their geometric properties when addition is replaced with minimization and multiplication is replaced with ordinary addition: : x\oplus y=\min\, : x\otimes y=x+y. So for example, the classical polynomial x^3+xy+y^4 would become \min\. Such polynomials and their solutions have important applications in optimization problems, for example the problem of optimizing departure times for a network of trains. Tropical geometry is a variant of algebraic geometry in which polynomial graphs resemble piecewise linear meshes, and in which numbers belong to the tropical semiring instead of a field. Because classical and tropical geometry are closely related, results and methods can be converted between them. Algebraic varieties can be mapped to a tropical counterpart and, since this process still retains some geometric information about the original variety, it can be used to help prove and generalize classical results from ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algebraic Geometry
Algebraic geometry is a branch of mathematics which uses abstract algebraic techniques, mainly from commutative algebra, to solve geometry, geometrical problems. Classically, it studies zero of a function, zeros of multivariate polynomials; the modern approach generalizes this in a few different aspects. The fundamental objects of study in algebraic geometry are algebraic variety, algebraic varieties, which are geometric manifestations of solution set, solutions of systems of polynomial equations. Examples of the most studied classes of algebraic varieties are line (geometry), lines, circles, parabolas, ellipses, hyperbolas, cubic curves like elliptic curves, and quartic curves like lemniscate of Bernoulli, lemniscates and Cassini ovals. These are plane algebraic curves. A point of the plane lies on an algebraic curve if its coordinates satisfy a given polynomial equation. Basic questions involve the study of points of special interest like singular point of a curve, singular p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lunar Arithmetic
Lunar most commonly means "of or relating to the Moon The Moon is Earth's only natural satellite. It Orbit of the Moon, orbits around Earth at Lunar distance, an average distance of (; about 30 times Earth diameter, Earth's diameter). The Moon rotation, rotates, with a rotation period (lunar ...". Lunar may also refer to: Arts and entertainment * ''Lunar'' (series), a series of video games * "Lunar" (song), by David Guetta * "Lunar", a song by Priestess from the 2009 album '' Prior to the Fire'' * Lunar Drive-in Theatre, in Dandenong, Victoria, Australia * Lunars, a fictional race in the series '' The Lunar Chronicles'' by Marissa Meyer Other uses * Lunar dynasty, a legendary house of warrior–rulers in ancient Indian texts * Lunar Magic, Super Mario World level editor * Lunar Design, or LUNAR, a San Francisco-based design consultancy * Hasselblad Lunar, a digital camera * Lunar, a brandname of Ethinylestradiol/cyproterone acetate, a birth control pill * Luna ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tropical Analysis
In the mathematical discipline of idempotent analysis, tropical analysis is the study of the tropical semiring. Applications The max tropical semiring can be used appropriately to determine marking times within a given Petri net and a vector filled with marking state at the beginning: -\infty (unit for max, tropical addition) means "never before", while 0 (unit for addition, tropical multiplication) is "no additional time". Tropical cryptography is cryptography based on the tropical semiring. Tropical geometry is an analog to algebraic geometry, using the tropical semiring. References * Further reading * * See also *Lunar arithmetic Lunar most commonly means "of or relating to the Moon The Moon is Earth's only natural satellite. It Orbit of the Moon, orbits around Earth at Lunar distance, an average distance of (; about 30 times Earth diameter, Earth's diameter). Th ... External links MaxPlus algebraworking group, INRIA Rocquencourt {{Mathanalysi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |