|
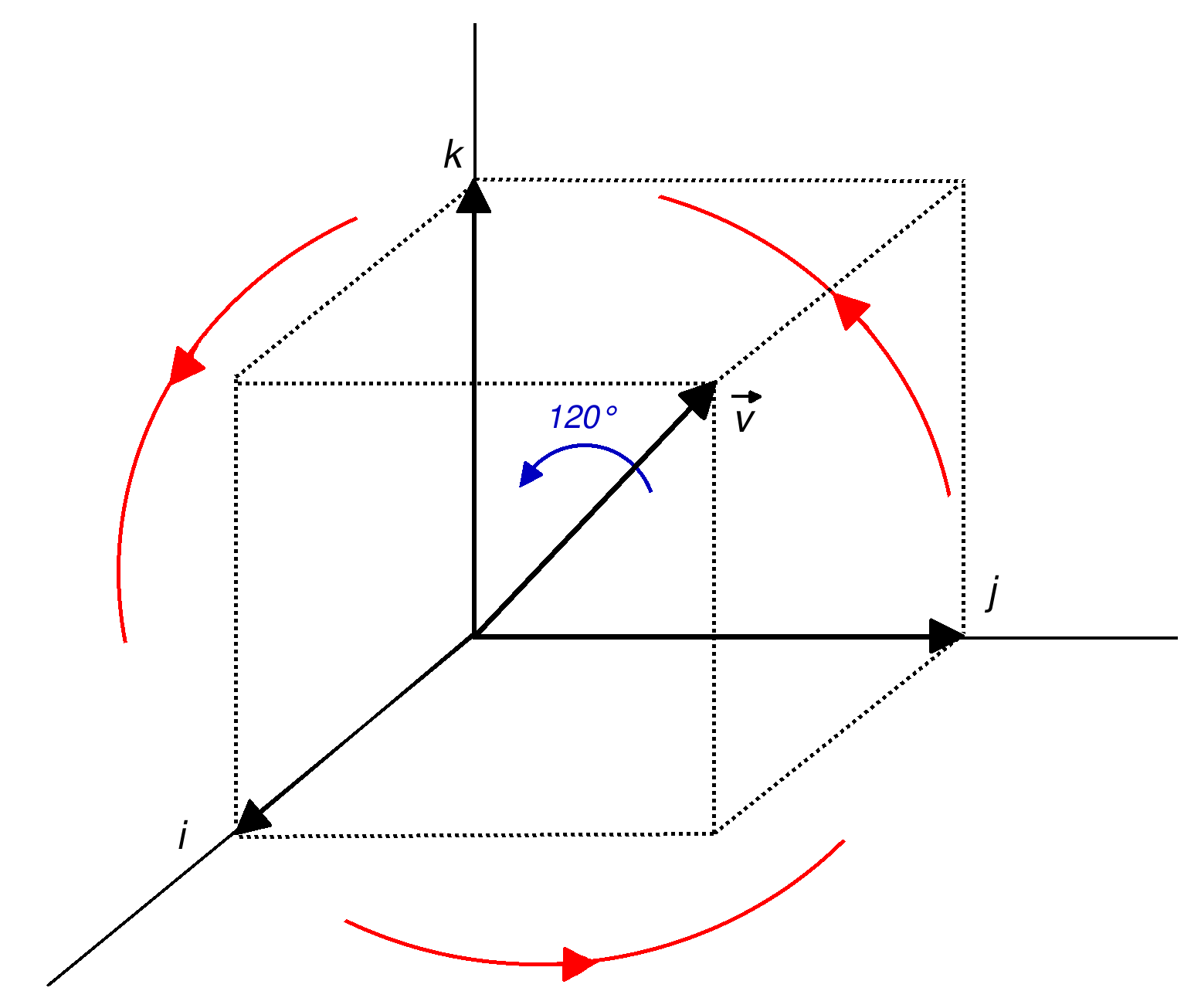
Quaternions
In mathematics, the quaternion number system extends the complex numbers. Quaternions were first described by the Irish mathematician William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space. The algebra of quaternions is often denoted by (for ''Hamilton''), or in blackboard bold by \mathbb H. Quaternions are not a field, because multiplication of quaternions is not, in general, commutative. Quaternions provide a definition of the quotient of two vectors in a three-dimensional space. Quaternions are generally represented in the form a + b\,\mathbf i + c\,\mathbf j +d\,\mathbf k, where the coefficients , , , are real numbers, and , are the ''basis vectors'' or ''basis elements''. Quaternions are used in pure mathematics, but also have practical uses in applied mathematics, particularly for calculations involving three-dimensional rotations, such as in three-dimensional computer graphics, computer vision, robotics, magnetic resonance imaging and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quaternions And Spatial Rotation
unit vector, Unit quaternions, known as versor, ''versors'', provide a convenient mathematics, mathematical notation for representing spatial Orientation (geometry), orientations and rotations of elements in three dimensional space. Specifically, they encode information about an Axis–angle representation, axis-angle rotation about an arbitrary axis. Rotation and orientation quaternions have applications in computer graphics, Presented at SIGGRAPH '85. computer vision, robotics, navigation, molecular dynamics, flight dynamics, orbital mechanics of satellites, and Texture (crystalline), crystallographic texture analysis. When used to represent rotation, unit quaternions are also called rotation quaternions as they represent the 3D rotation group. When used to represent an Orientation (geometry), orientation (rotation relative to a reference coordinate system), they are called orientation quaternions or attitude quaternions. A spatial rotation around a fixed point of \theta radians ab ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
William Rowan Hamilton
Sir William Rowan Hamilton (4 August 1805 – 2 September 1865) was an Irish astronomer, mathematician, and physicist who made numerous major contributions to abstract algebra, classical mechanics, and optics. His theoretical works and mathematical equations are considered fundamental to modern theoretical physics, particularly Hamiltonian mechanics, his reformulation of Lagrangian mechanics. His career included the analysis of geometrical optics, Fourier analysis, and quaternions, the last of which made him one of the founders of modern linear algebra. Hamilton was Andrews Professor of Astronomy at Trinity College Dublin. He was also the third director of Dunsink Observatory from 1827 to 1865. The Hamilton Institute at Maynooth University is named after him. Early life Hamilton was the fourth of nine children born to Sarah Hutton (1780–1817) and Archibald Hamilton (1778–1819), who lived in Dublin at 29 Dominick Street, Dublin, Dominick Street, later renumbered to 36. Ham ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euler Angles
The Euler angles are three angles introduced by Leonhard Euler to describe the Orientation (geometry), orientation of a rigid body with respect to a fixed coordinate system.Novi Commentarii academiae scientiarum Petropolitanae 20, 1776, pp. 189–207 (E478PDF/ref> They can also represent the orientation of a mobile frame of reference in physics or the orientation of a general Basis (linear algebra), basis in three dimensional linear algebra. Classic Euler angles usually take the inclination angle in such a way that zero degrees represent the vertical orientation. Alternative forms were later introduced by Peter Guthrie Tait and George H. Bryan intended for use in aeronautics and engineering in which zero degrees represent the horizontal position. Chained rotations equivalence Euler angles can be defined by elemental geometry or by composition of rotations (i.e. chained rotations). The geometrical definition demonstrates that three consecutive ''elemental rotations'' (rotatio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Frobenius Theorem (real Division Algebras)
In mathematics, more specifically in abstract algebra, the Frobenius theorem, proved by Ferdinand Georg Frobenius in 1877, characterizes the finite-dimensional associative division algebras over the real numbers. According to the theorem, every such algebra is isomorphic to one of the following: * (the real numbers) * (the complex numbers) * (the quaternions) These algebras have real dimension , and , respectively. Of these three algebras, and are commutative, but is not. Proof The main ingredients for the following proof are the Cayley–Hamilton theorem and the fundamental theorem of algebra. Introducing some notation * Let be the division algebra in question. * Let be the dimension of . * We identify the real multiples of with . * When we write for an element of , we imply that is contained in . * We can consider as a finite-dimensional -vector space. Any element of defines an endomorphism of by left-multiplication, we identify with that endomorphism. Th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Clifford Algebra
In mathematics, a Clifford algebra is an algebra generated by a vector space with a quadratic form, and is a unital associative algebra with the additional structure of a distinguished subspace. As -algebras, they generalize the real numbers, complex numbers, quaternions and several other hypercomplex number systems. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal transformations. Clifford algebras have important applications in a variety of fields including geometry, theoretical physics and digital image processing. They are named after the English mathematician William Kingdon Clifford (1845–1879). The most familiar Clifford algebras, the orthogonal Clifford algebras, are also referred to as (''pseudo-'')''Riemannian Clifford algebras'', as distinct from ''symplectic Clifford algebras''. Introduction and basic properties A Clifford algebra is a unital associative algebra that contains and is generated by ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Composition Algebra
In mathematics, a composition algebra over a field is a not necessarily associative algebra over together with a nondegenerate quadratic form that satisfies :N(xy) = N(x)N(y) for all and in . A composition algebra includes an involution called a conjugation: x \mapsto x^*. The quadratic form N(x) = x x^* is called the norm of the algebra. A composition algebra (''A'', ∗, ''N'') is either a division algebra or a split algebra, depending on the existence of a non-zero ''v'' in ''A'' such that ''N''(''v'') = 0, called a null vector. When ''x'' is ''not'' a null vector, the multiplicative inverse of ''x'' is When there is a non-zero null vector, ''N'' is an isotropic quadratic form, and "the algebra splits". Structure theorem Every unital composition algebra over a field can be obtained by repeated application of the Cayley–Dickson construction starting from (if the characteristic of is different from ) or a 2-dimensional composition subalgebra (if ). The ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rotation Matrix
In linear algebra, a rotation matrix is a transformation matrix that is used to perform a rotation (mathematics), rotation in Euclidean space. For example, using the convention below, the matrix :R = \begin \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end rotates points in the plane counterclockwise through an angle about the origin of a two-dimensional Cartesian coordinate system. To perform the rotation on a plane point with standard coordinates , it should be written as a column vector, and matrix multiplication, multiplied by the matrix : : R\mathbf = \begin \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end \begin x \\ y \end = \begin x\cos\theta-y\sin\theta \\ x\sin\theta+y\cos\theta \end. If and are the coordinates of the endpoint of a vector with the length ''r'' and the angle \phi with respect to the -axis, so that x = r \cos \phi and y = r \sin \phi, then the above equations become the List of trigonometric identities#Angle sum and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cayley Q8 Multiplication Graph
Cayley may refer to: __NOTOC__ People * Cayley (surname) * Cayley Illingworth (1759–1823), Anglican Archdeacon of Stow * Cayley Mercer (born 1994), Canadian women's ice hockey player Places * Cayley, Alberta, Canada, a hamlet ** Cayley/A. J. Flying Ranch Airport * Mount Cayley, a volcano in southwestern British Columbia, Canada * Cayley Glacier, Graham Land, Antarctica * Cayley (crater), a lunar crater Other uses * Cayley baronets, a title in the Baronetage of England * Cayley computer algebra system, designed to solve mathematical problems, particularly in group theory See also * W. Cayley Hamilton (died 1891), Canadian barrister and politician * Caylee (name), given name * Cèilidh, traditional Scottish or Irish social gathering * Kaylee, given name * Kaley (other) * Kayleigh (other) {{disambig, geo, given name ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Magnetic Resonance Imaging
Magnetic resonance imaging (MRI) is a medical imaging technique used in radiology to generate pictures of the anatomy and the physiological processes inside the body. MRI scanners use strong magnetic fields, magnetic field gradients, and radio waves to form images of the organs in the body. MRI does not involve X-rays or the use of ionizing radiation, which distinguishes it from computed tomography (CT) and positron emission tomography (PET) scans. MRI is a medical application of nuclear magnetic resonance (NMR) which can also be used for imaging in other NMR applications, such as NMR spectroscopy. MRI is widely used in hospitals and clinics for medical diagnosis, staging and follow-up of disease. Compared to CT, MRI provides better contrast in images of soft tissues, e.g. in the brain or abdomen. However, it may be perceived as less comfortable by patients, due to the usually longer and louder measurements with the subject in a long, confining tube, although ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Subring
In mathematics, a subring of a ring is a subset of that is itself a ring when binary operations of addition and multiplication on ''R'' are restricted to the subset, and that shares the same multiplicative identity as .In general, not all subsets of a ring are rings. Definition A subring of a ring is a subset of that preserves the structure of the ring, i.e. a ring with . Equivalently, it is both a subgroup of and a submonoid of . Equivalently, is a subring if and only if it contains the multiplicative identity of , and is closed under multiplication and subtraction. This is sometimes known as the ''subring test''. Variations Some mathematicians define rings without requiring the existence of a multiplicative identity (see '). In this case, a subring of is a subset of that is a ring for the operations of (this does imply it contains the additive identity of ). This alternate definition gives a strictly weaker condition, even for rings that do have a mult ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Classification Of Clifford Algebras
In abstract algebra, in particular in the theory of nondegenerate quadratic forms on vector spaces, the finite-dimensional real and complex Clifford algebras for a nondegenerate quadratic form have been completely classified as rings. In each case, the Clifford algebra is algebra isomorphic to a full matrix ring over R, C, or H (the quaternions), or to a direct sum of two copies of such an algebra, though not in a canonical way. Below it is shown that distinct Clifford algebras may be algebra-isomorphic, as is the case of Cl1,1(R) and Cl2,0(R), which are both isomorphic as rings to the ring of two-by-two matrices over the real numbers. Notation and conventions The Clifford product is the manifest ring product for the Clifford algebra, and all algebra homomorphisms in this article are with respect to this ring product. Other products defined within Clifford algebras, such as the exterior product, and other structure, such as the distinguished subspace of generators ''V'', ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Domain (ring Theory)
In algebra, a domain is a nonzero ring in which implies or .Lam (2001), p. 3 (Sometimes such a ring is said to "have the zero-product property".) Equivalently, a domain is a ring in which 0 is the only left zero divisor (or equivalently, the only right zero divisor). A commutative domain is called an integral domain. Mathematical literature contains multiple variants of the definition of "domain".Some authors also consider the zero ring to be a domain: see Polcino M. & Sehgal (2002), p. 65. Some authors apply the term "domain" also to rngs with the zero-product property; such authors consider ''n''Z to be a domain for each positive integer ''n'': see Lanski (2005), p. 343. But integral domains are always required to be nonzero and to have a 1. Examples and non-examples * The ring \mathbb/6\mathbb is not a domain, because the images of 2 and 3 in this ring are nonzero elements with product 0. More generally, for a positive integer n, the ring \mathbb/n\mathbb is a d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |