|
Quadrilaterals
In geometry a quadrilateral is a four-sided polygon, having four edges (sides) and four corners (vertices). The word is derived from the Latin words ''quadri'', a variant of four, and ''latus'', meaning "side". It is also called a tetragon, derived from Greek "tetra" meaning "four" and "gon" meaning "corner" or "angle", in analogy to other polygons (e.g. pentagon). Since "gon" means "angle", it is analogously called a quadrangle, or 4-angle. A quadrilateral with vertices A, B, C and D is sometimes denoted as \square ABCD. Quadrilaterals are either simple (not self-intersecting), or complex (self-intersecting, or crossed). Simple quadrilaterals are either convex or concave. The interior angles of a simple (and planar) quadrilateral ''ABCD'' add up to 360 degrees, that is :\angle A+\angle B+\angle C+\angle D=360^. This is a special case of the ''n''-gon interior angle sum formula: ''S'' = (''n'' − 2) × 180° (here, n=4). All non-self-crossing quadrilaterals tile the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kite (geometry)
In Euclidean geometry, a kite is a quadrilateral with reflection symmetry across a diagonal. Because of this symmetry, a kite has two equal angles and two pairs of adjacent equal-length sides. Kites are also known as deltoids, but the word ''deltoid'' may also refer to a deltoid curve, an unrelated geometric object sometimes studied in connection with quadrilaterals.See H. S. M. Coxeter's review of in : "It is unfortunate that the author uses, instead of 'kite', the name 'deltoid', which belongs more properly to a curve, the three-cusped hypocycloid." A kite may also be called a dart, particularly if it is not convex. Every kite is an orthodiagonal quadrilateral (its diagonals are at right angles) and, when convex, a tangential quadrilateral (its sides are tangent to an inscribed circle). The convex kites are exactly the quadrilaterals that are both orthodiagonal and tangential. They include as special cases the right kites, with two opposite right angles; the rhombus, rhombi, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Square (geometry)
In geometry, a square is a regular quadrilateral. It has four straight sides of equal length and four equal angles. Squares are special cases of rectangles, which have four equal angles, and of rhombuses, which have four equal sides. As with all rectangles, a square's angles are right angles (90 degrees, or /2 radians), making adjacent sides perpendicular. The area of a square is the side length multiplied by itself, and so in algebra, multiplying a number by itself is called squaring. Equal squares can tile the plane edge-to-edge in the square tiling. Square tilings are ubiquitous in tiled floors and walls, graph paper, image pixels, and game boards. Square shapes are also often seen in building floor plans, origami paper, food servings, in graphic design and heraldry, and in instant photos and fine art. The formula for the area of a square forms the basis of the calculation of area and motivates the search for methods for squaring the circle by compass and straightedge ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rectangle
In Euclidean geometry, Euclidean plane geometry, a rectangle is a Rectilinear polygon, rectilinear convex polygon or a quadrilateral with four right angles. It can also be defined as: an equiangular quadrilateral, since equiangular means that all of its angles are equal (360°/4 = 90°); or a parallelogram containing a right angle. A rectangle with four sides of equal length is a ''square''. The term "wikt:oblong, oblong" is used to refer to a non-square rectangle. A rectangle with Vertex (geometry), vertices ''ABCD'' would be denoted as . The word rectangle comes from the Latin ''rectangulus'', which is a combination of ''rectus'' (as an adjective, right, proper) and ''angulus'' (angle). A #Crossed rectangles, crossed rectangle is a crossed (self-intersecting) quadrilateral which consists of two opposite sides of a rectangle along with the two diagonals (therefore only two sides are parallel). It is a special case of an antiparallelogram, and its angles are not right angles an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
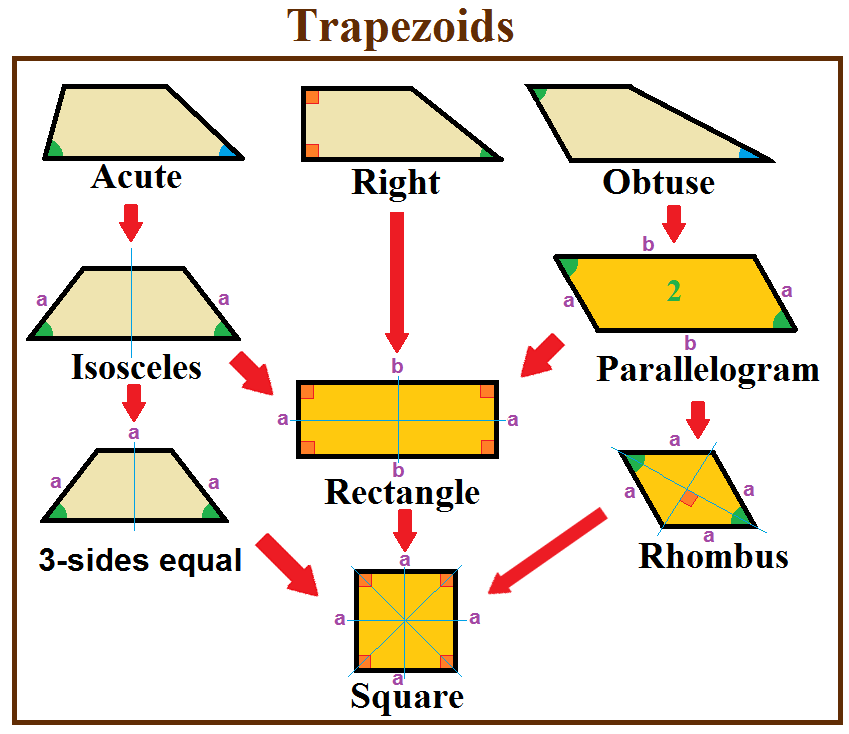
Isosceles Trapezoid
In Euclidean geometry, an isosceles trapezoid is a convex quadrilateral with a line of symmetry bisecting one pair of opposite sides. It is a special case of a trapezoid. Alternatively, it can be defined as a trapezoid in which both legs and both base angles are of equal measure, or as a trapezoid whose diagonals have equal length. Note that a non-rectangular parallelogram is not an isosceles trapezoid because of the second condition, or because it has no line of symmetry. In any isosceles trapezoid, two opposite sides (the bases) are parallel, and the two other sides (the legs) are of equal length (properties shared with the parallelogram), and the diagonals have equal length. The base angles of an isosceles trapezoid are equal in measure (there are in fact two pairs of equal base angles, where one base angle is the supplementary angle of a base angle at the other base). Special cases Trapezoid is defined as a quadrilateral having exactly one pair of parallel sides, with the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Trapezoid
In geometry, a trapezoid () in North American English, or trapezium () in British English, is a quadrilateral that has at least one pair of parallel sides. The parallel sides are called the ''bases'' of the trapezoid. The other two sides are called the ''legs'' or ''lateral sides''. (If the trapezoid is a parallelogram, then the choice of bases and legs is arbitrary.) A trapezoid is usually considered to be a convex quadrilateral in Euclidean geometry, but there are also crossed cases. If ''ABCD'' is a convex trapezoid, then ''ABDC'' is a crossed trapezoid. The metric formulas in this article apply in convex trapezoids. Definitions ''Trapezoid'' can be defined exclusively or inclusively. Under an exclusive definition a trapezoid is a quadrilateral having pair of parallel sides, with the other pair of opposite sides non-parallel. Parallelograms including rhombi, rectangles, and squares are then not considered to be trapezoids. Under an inclusive definition, a trapezoid is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rhombus
In plane Euclidean geometry, a rhombus (: rhombi or rhombuses) is a quadrilateral whose four sides all have the same length. Another name is equilateral quadrilateral, since equilateral means that all of its sides are equal in length. The rhombus is often called a "diamond", after the Diamonds (suit), diamonds suit in playing cards which resembles the projection of an Octahedron#Orthogonal projections, octahedral diamond, or a lozenge (shape), lozenge, though the former sometimes refers specifically to a rhombus with a 60° angle (which some authors call a calisson after calisson, the French sweet—also see Polyiamond), and the latter sometimes refers specifically to a rhombus with a 45° angle. Every rhombus is simple polygon, simple (non-self-intersecting), and is a special case of a parallelogram and a Kite (geometry), kite. A rhombus with right angles is a square. Etymology The word "rhombus" comes from , meaning something that spins, which derives from the verb , roman ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parallelogram
In Euclidean geometry, a parallelogram is a simple polygon, simple (non-list of self-intersecting polygons, self-intersecting) quadrilateral with two pairs of Parallel (geometry), parallel sides. The opposite or facing sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of equal measure. The congruence (geometry), congruence of opposite sides and opposite angles is a direct consequence of the Euclidean parallel postulate and neither condition can be proven without appealing to the Euclidean parallel postulate or one of its equivalent formulations. By comparison, a quadrilateral with at least one pair of parallel sides is a trapezoid in American English or a trapezium in British English. The three-dimensional counterpart of a parallelogram is a parallelepiped. The word "parallelogram" comes from the Greek παραλληλό-γραμμον, ''parallēló-grammon'', which means "a shape of parallel lines". Special cases *Rectangle – A par ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
North American English
North American English (NAmE) encompasses the English language as spoken in both the United States and Canada. Because of their related histories and cultures, plus the similarities between the pronunciations (accents), vocabulary, and grammar of American English, U.S. English and Canadian English, linguists often group the two together. Canadians are generally tolerant of both British and American spellings, although certain words always take British spellings (e.g., ''cheque'') and others American spellings (e.g., ''tire'' rather than ''tyre''). Dialects of English spoken by United Empire Loyalists who fled the American Revolution (1775–1783) have had a large influence on Canadian English from its early roots. Some terms in North American English are used almost exclusively in Canada and the United States (for example, the terms ''diaper'' and ''gasoline'' are widely used instead of ''nappy'' and ''petrol''). Although many English speakers from outside North America regard ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Oblong
An oblong is an object longer than it is wide, especially a non-square rectangle. Oblong may also refer to: Places * Oblong, Illinois, a village in the United States * Oblong Township, Crawford County, Illinois, United States * A strip of land on the New York-Connecticut border in the United States nicknamed the "Oblong", running north from the Connecticut panhandle Other uses * Oblong (company), an American a cloud-based communication service provider * Oblong Industries, a spin-off of the MIT Media Lab * Angus Oblong, American author and actor born David Walker (born 1976) * '' The Oblongs'', a short-lived 2001 American animated television program co-created by Angus Oblong * Bob Oblong, a character in '' The Shapies'', an Australian animated children's television series * Oblong, a leaf shape The following terms are used to describe leaf morphology in the description and taxonomy of plants. Leaves may be simple (that is, the leaf blade or 'lamina' is undivided) or com ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Angle
In Euclidean geometry, an angle can refer to a number of concepts relating to the intersection of two straight Line (geometry), lines at a Point (geometry), point. Formally, an angle is a figure lying in a Euclidean plane, plane formed by two Ray (geometry), rays, called the ''Side (plane geometry), sides'' of the angle, sharing a common endpoint, called the ''vertex (geometry), vertex'' of the angle. More generally angles are also formed wherever two lines, rays or line segments come together, such as at the corners of triangles and other polygons. An angle can be considered as the region of the plane bounded by the sides. Angles can also be formed by the intersection of two planes or by two intersecting curves, in which case the rays lying tangent to each curve at the point of intersection define the angle. The term ''angle'' is also used for the size, magnitude (mathematics), magnitude or Physical quantity, quantity of these types of geometric figures and in this context an a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |