 |
Percolation Theory
In statistical physics and mathematics, percolation theory describes the behavior of a network when nodes or links are added. This is a geometric type of phase transition, since at a critical fraction of addition the network of small, disconnected clusters merge into significantly larger Glossary of graph theory, connected, so-called spanning clusters. The applications of percolation theory to materials science and in many other disciplines are discussed here and in the articles Network theory and Percolation (cognitive psychology). Introduction A representative question (and the etymology, source of the name) is as follows. Assume that some liquid is poured on top of some porosity, porous material. Will the liquid be able to make its way from hole to hole and reach the bottom? This physical question is mathematical model, modelled mathematically as a Grid graph, three-dimensional network of graph (discrete mathematics), vertices, usually called "sites", in which the graph (dis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
 |
Statistical Physics
In physics, statistical mechanics is a mathematical framework that applies statistical methods and probability theory to large assemblies of microscopic entities. Sometimes called statistical physics or statistical thermodynamics, its applications include many problems in a wide variety of fields such as biology, neuroscience, computer science, information theory and sociology. Its main purpose is to clarify the properties of matter in aggregate, in terms of physical laws governing atomic motion. Statistical mechanics arose out of the development of classical thermodynamics, a field for which it was successful in explaining macroscopic physical properties—such as temperature, pressure, and heat capacity—in terms of microscopic parameters that fluctuate about average values and are characterized by probability distributions. While classical thermodynamics is primarily concerned with thermodynamic equilibrium, statistical mechanics has been applied in non-equilibrium stat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Infinite Graph
This is a glossary of graph theory. Graph theory is the study of graphs, systems of nodes or vertices connected in pairs by lines or edges. Symbols A B C D E F G H I J K L M ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Tree (graph Theory)
In graph theory, a tree is an undirected graph in which any two vertices are connected by path, or equivalently a connected acyclic undirected graph. A forest is an undirected graph in which any two vertices are connected by path, or equivalently an acyclic undirected graph, or equivalently a disjoint union of trees. A directed tree, oriented tree,See .See . polytree,See . or singly connected networkSee . is a directed acyclic graph (DAG) whose underlying undirected graph is a tree. A polyforest (or directed forest or oriented forest) is a directed acyclic graph whose underlying undirected graph is a forest. The various kinds of data structures referred to as trees in computer science have underlying graphs that are trees in graph theory, although such data structures are generally rooted trees. A rooted tree may be directed, called a directed rooted tree, either making all its edges point away from the root—in which case it is called an arborescence or out-tree� ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Coordination Number
In chemistry, crystallography, and materials science, the coordination number, also called ligancy, of a central atom in a molecule or crystal is the number of atoms, molecules or ions bonded to it. The ion/molecule/atom surrounding the central ion/molecule/atom is called a ligand. This number is determined somewhat differently for molecules than for crystals. For molecules and polyatomic ions the coordination number of an atom is determined by simply counting the other atoms to which it is bonded (by either single or multiple bonds). For example, [Cr(NH3)2Cl2Br2]− has Cr3+ as its central cation, which has a coordination number of 6 and is described as ''hexacoordinate''. The common coordination numbers are 4, 6 and 8. Molecules, polyatomic ions and coordination complexes In chemistry, coordination number, defined originally in 1893 by Alfred Werner, is the total number of neighbors of a central atom in a molecule or ion. The concept is most commonly applied to coordination ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Bethe Lattice
In statistical mechanics and mathematics, the Bethe lattice (also called a regular tree) is an infinite symmetric regular tree where all vertices have the same number of neighbors. The Bethe lattice was introduced into the physics literature by Hans Bethe in 1935. In such a graph, each node is connected to ''z'' neighbors; the number ''z'' is called either the coordination number or the degree, depending on the field. Due to its distinctive topological structure, the statistical mechanics of lattice models on this graph are often easier to solve than on other lattices. The solutions are related to the often used Bethe ansatz for these systems. Basic properties When working with the Bethe lattice, it is often convenient to mark a given vertex as the root, to be used as a reference point when considering local properties of the graph. Sizes of layers Once a vertex is marked as the root, we can group the other vertices into layers based on their distance from the root. The n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Harry Kesten
Harry Kesten (November 19, 1931 – March 29, 2019) was a Jewish American mathematician best known for his work in probability, most notably on random walks on groups and graphs, random matrices, branching processes, and percolation theory. Biography Harry Kesten was born in Duisburg, Germany in 1931, and grew up in the Netherlands, where he moved with his parents in 1933 to escape the Nazis. Surviving the Holocaust, Kesten initially studied chemistry, and later theoretical physics and mathematics, at the University of Amsterdam. He moved to the United States in 1956 and received his PhD in Mathematics in 1958 at Cornell University under the supervision of Mark Kac. He was an instructor at Princeton University and the Hebrew University before returning to Cornell in 1961. Kesten died on March 29, 2019, in Ithaca at the age of 87. Mathematical work Kesten's work includes many fundamental contributions across almost the whole of probability, including the following highli ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Square Lattice
In mathematics, the square lattice is a type of lattice in a two-dimensional Euclidean space. It is the two-dimensional version of the integer lattice, denoted as . It is one of the five types of two-dimensional lattices as classified by their symmetry groups; its symmetry group in IUC notation as , Coxeter notation as , and orbifold notation as . Two orientations of an image of the lattice are by far the most common. They can conveniently be referred to as the upright square lattice and diagonal square lattice; the latter is also called the centered square lattice.. They differ by an angle of 45°. This is related to the fact that a square lattice can be partitioned into two square sub-lattices, as is evident in the colouring of a checkerboard. Symmetry The square lattice's symmetry category is wallpaper group . A pattern with this lattice of translational symmetry cannot have more, but may have less symmetry than the lattice itself. An upright square lattice can be vi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
John Hammersley
John Michael Hammersley, (21 March 1920 – 2 May 2004) was a British mathematician best known for his foundational work in the theory of self-avoiding walks and percolation theory. Early life and education Hammersley was born in Helensburgh in Dunbartonshire, and educated at Sedbergh School. He started reading mathematics at Emmanuel College, Cambridge but was called up to join the Royal Artillery in 1941. During his time in the army he worked on ballistics. He graduated in mathematics in 1948. He never studied for a PhD but was awarded an ScD by Cambridge University and a DSc by Oxford University in 1959. Academic career With Jillian Beardwood and J.H. Halton, Hammersley is known for the Beardwood-Halton-Hammersley Theorem. Published by the Cambridge Philosophical Society in a 1959 article entitled “The Shortest Path Through Many Points,” the theorem provides a practical solution to the “traveling salesman problem.” He held a number of positions, both in and outs ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Monte Carlo Method
Monte Carlo methods, or Monte Carlo experiments, are a broad class of computational algorithms that rely on repeated random sampling to obtain numerical results. The underlying concept is to use randomness to solve problems that might be deterministic in principle. The name comes from the Monte Carlo Casino in Monaco, where the primary developer of the method, mathematician Stanisław Ulam, was inspired by his uncle's gambling habits. Monte Carlo methods are mainly used in three distinct problem classes: optimization, numerical integration, and generating draws from a probability distribution. They can also be used to model phenomena with significant uncertainty in inputs, such as calculating the risk of a nuclear power plant failure. Monte Carlo methods are often implemented using computer simulations, and they can provide approximate solutions to problems that are otherwise intractable or too complex to analyze mathematically. Monte Carlo methods are widely used in va ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
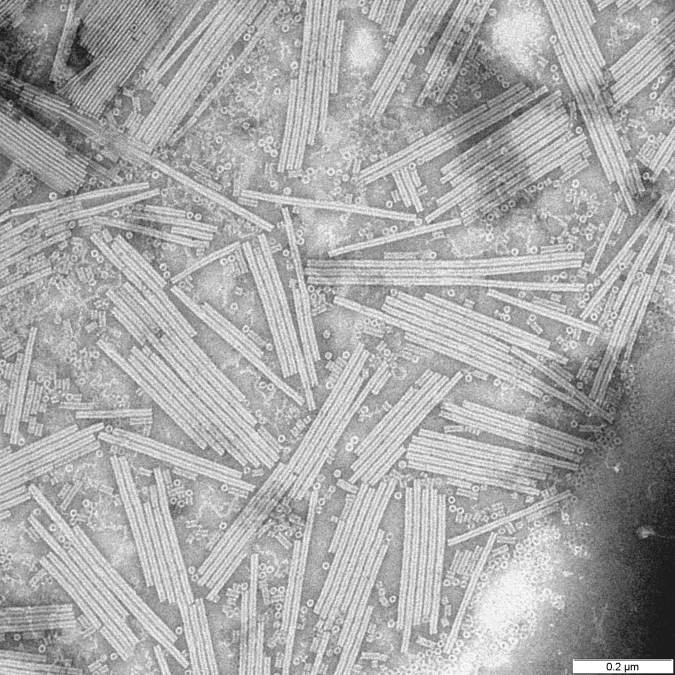 |
Rosalind Franklin
Rosalind Elsie Franklin (25 July 192016 April 1958) was a British chemist and X-ray crystallographer. Her work was central to the understanding of the molecular structures of DNA (deoxyribonucleic acid), RNA (ribonucleic acid), viruses, coal, and graphite. Although her works on coal and viruses were appreciated in her lifetime, Franklin's contributions to the discovery of the structure of DNA were largely unrecognised during her life, for which Franklin has been variously referred to as the "wronged heroine", the "dark lady of DNA", the "forgotten heroine", a "feminist icon", and the "Sylvia Plath of molecular biology". Franklin graduated in 1941 with a degree in Natural Sciences (Cambridge), natural sciences from Newnham College, Cambridge, and then enrolled for a PhD in physical chemistry under Ronald George Wreyford Norrish, the 1920 Chair of Physical Chemistry at the University of Cambridge. Disappointed by Norrish's lack of enthusiasm, she took up a research position und ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
British Coal Utilisation Research Association
British Coal Utilisation Research Association (BCURA) was a non-profit association of industrial companies, incorporated 23 April 1938 and dissolved 24 February 2015. History It was founded in 1938, with an assured income of £25000 per year for five years, supplied by the Mining Association of Great Britain and a grant from the government Department of Scientific and Industrial Research, establishing a research station in West Brompton. It was formed from the research department of the Combustion (''formerly Coal-burning'') Appliance Manufacturer's Association becoming a separate entity. Laboratories were also later established in Leatherhead. The first Director was John G. Bennett. During the Second World War it developed small units for the manufacture of producer gas from coal to use in vehicles in place of petrol. A £1000,000 five-year programme was also begun with a view not only to the needs of wartime but also for industry afterwards with fuels and chemicals from c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Flory–Stockmayer Theory
Flory–Stockmayer theory is a theory governing the cross-linking and gelation of step-growth polymers.Flory, P.J. (1941). "Molecular Size Distribution in Three Dimensional Polymers I. Gelation". ''J. Am. Chem. Soc.'' 63, 3083 The Flory–Stockmayer theory represents an advancement from the Carothers equation, allowing for the identification of the gel point for polymer synthesis not at stoichiometric balance. The theory was initially conceptualized by Paul Flory in 1941 and then was further developed by Walter Stockmayer in 1944 to include cross-linking with an arbitrary initial size distribution.Stockmayer, Walter H.(1944). "Theory of Molecular Size Distribution and Gel Formation in Branched Polymers II. General Cross Linking". ''Journal of Chemical Physics.'' 12,4, 125 The Flory–Stockmayer theory was the first theory investigating percolation processes. Flory–Stockmayer theory is a special case of random graph theory of gelation. History Gelation occurs when a polymer f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |