|
Multivariate Statistics
Multivariate statistics is a subdivision of statistics encompassing the simultaneous observation and analysis of more than one outcome variable, i.e., '' multivariate random variables''. Multivariate statistics concerns understanding the different aims and background of each of the different forms of multivariate analysis, and how they relate to each other. The practical application of multivariate statistics to a particular problem may involve several types of univariate and multivariate analyses in order to understand the relationships between variables and their relevance to the problem being studied. In addition, multivariate statistics is concerned with multivariate probability distributions, in terms of both :*how these can be used to represent the distributions of observed data; :*how they can be used as part of statistical inference, particularly where several different quantities are of interest to the same analysis. Certain types of problems involving multivariate da ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistics
Statistics (from German language, German: ', "description of a State (polity), state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of statistical survey, surveys and experimental design, experiments. When census data (comprising every member of the target population) cannot be collected, statisticians collect data by developing specific experiment designs and survey sample (statistics), samples. Representative sampling assures that inferences and conclusions can reasonably extend from the sample ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multivariate Analysis Of Covariance
Multivariate analysis of covariance (MANCOVA) is an extension of analysis of covariance ( ANCOVA) methods to cover cases where there is more than one dependent variable and where the control of concomitant continuous independent variables – covariates – is required. The most prominent benefit of the MANCOVA design over the simple MANOVA is the 'factoring out' of noise or error that has been introduced by the covariant. A commonly used multivariate version of the ANOVA F-statistic is Wilks' Lambda (Λ), which represents the ratio between the error variance (or covariance) and the effect variance (or covariance). Statsoft Textbook, ANOVA/MANOVA. Goals Similarly to all tests in the ANOVA family, the primary aim of the MANCOVA is to tes ...[...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
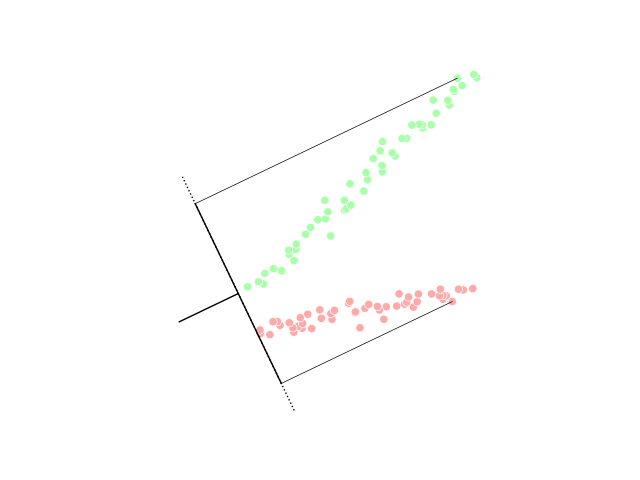
Linear Discriminant Analysis
Linear discriminant analysis (LDA), normal discriminant analysis (NDA), canonical variates analysis (CVA), or discriminant function analysis is a generalization of Fisher's linear discriminant, a method used in statistics and other fields, to find a linear combination of features that characterizes or separates two or more classes of objects or events. The resulting combination may be used as a linear classifier, or, more commonly, for dimensionality reduction before later statistical classification, classification. LDA is closely related to analysis of variance (ANOVA) and regression analysis, which also attempt to express one dependent variable as a linear combination of other features or measurements. However, ANOVA uses categorical variable, categorical independent variables and a continuous variable, continuous dependent variable, whereas discriminant analysis has continuous independent variables and a categorical dependent variable (''i.e.'' the class label). Logistic regr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Principal Coordinates Analysis
Multidimensional scaling (MDS) is a means of visualizing the level of similarity of individual cases of a data set. MDS is used to translate distances between each pair of n objects in a set into a configuration of n points mapped into an abstract Cartesian space. More technically, MDS refers to a set of related ordination techniques used in information visualization, in particular to display the information contained in a distance matrix. It is a form of non-linear dimensionality reduction. Given a distance matrix with the distances between each pair of objects in a set, and a chosen number of dimensions, ''N'', an MDS algorithm places each object into ''N''-dimensional space (a lower-dimensional representation) such that the between-object distances are preserved as well as possible. For ''N'' = 1, 2, and 3, the resulting points can be visualized on a scatter plot. Core theoretical contributions to MDS were made by James O. Ramsay of McGill University, who is also ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Canonical Correspondence Analysis
In multivariate analysis, canonical correspondence analysis (CCA) is an ordination technique that determines axes from the response data as a unimodal combination of measured predictors. CCA is commonly used in ecology in order to extract gradients that drive the composition of ecological communities. CCA extends correspondence analysis (CA) with regression, in order to incorporate predictor variables. History CCA was developed in 1986 by Cajo ter Braak and implemented in the program CANOCO, an extension of DECORANA. To date, CCA is one of the most popular multivariate methods in ecology, despite the availability of contemporary alternatives. CCA was originally derived and implemented using an algorithm of weighted averaging, though Legendre & Legendre (1998) derived an alternative algorithm. Assumptions The requirements of a CCA are that the samples are random and independent. Also, the data are categorical and that the independent variables are consistent within the sample ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Correspondence Analysis
Correspondence analysis (CA) is a multivariate statistical technique proposed by Herman Otto Hartley (Hirschfeld) and later developed by Jean-Paul Benzécri. It is conceptually similar to principal component analysis, but applies to categorical rather than continuous data. In a similar manner to principal component analysis, it provides a means of displaying or summarising a set of data in two-dimensional graphical form. Its aim is to display in a biplot any structure hidden in the multivariate setting of the data table. As such it is a technique from the field of multivariate ordination. Since the variant of CA described here can be applied either with a focus on the rows or on the columns it should in fact be called simple (symmetric) correspondence analysis. It is traditionally applied to the contingency table of a pair of nominal variables where each cell contains either a count or a zero value. If more than two categorical variables are to be summarized, a variant called ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Canonical Correlation Analysis
In statistics, canonical-correlation analysis (CCA), also called canonical variates analysis, is a way of inferring information from cross-covariance matrices. If we have two vectors ''X'' = (''X''1, ..., ''X''''n'') and ''Y'' = (''Y''1, ..., ''Y''''m'') of random variables, and there are correlations among the variables, then canonical-correlation analysis will find linear combinations of ''X'' and ''Y'' that have a maximum correlation with each other. T. R. Knapp notes that "virtually all of the commonly encountered parametric tests of significance can be treated as special cases of canonical-correlation analysis, which is the general procedure for investigating the relationships between two sets of variables." The method was first introduced by Harold Hotelling in 1936, although in the context of angles between flats the mathematical concept was published by Camille Jordan in 1875. CCA is now a cornerstone of multivariate statistics a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Factor Analysis
Factor analysis is a statistical method used to describe variability among observed, correlated variables in terms of a potentially lower number of unobserved variables called factors. For example, it is possible that variations in six observed variables mainly reflect the variations in two unobserved (underlying) variables. Factor analysis searches for such joint variations in response to unobserved latent variables. The observed variables are modelled as linear combinations of the potential factors plus "error" terms, hence factor analysis can be thought of as a special case of errors-in-variables models. Simply put, the factor loading of a variable quantifies the extent to which the variable is related to a given factor. A common rationale behind factor analytic methods is that the information gained about the interdependencies between observed variables can be used later to reduce the set of variables in a dataset. Factor analysis is commonly used in psychometrics, pers ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orthogonality
In mathematics, orthogonality is the generalization of the geometric notion of '' perpendicularity''. Although many authors use the two terms ''perpendicular'' and ''orthogonal'' interchangeably, the term ''perpendicular'' is more specifically used for lines and planes that intersect to form a right angle, whereas ''orthogonal'' is used in generalizations, such as ''orthogonal vectors'' or ''orthogonal curves''. ''Orthogonality'' is also used with various meanings that are often weakly related or not related at all with the mathematical meanings. Etymology The word comes from the Ancient Greek ('), meaning "upright", and ('), meaning "angle". The Ancient Greek (') and Classical Latin ' originally denoted a rectangle. Later, they came to mean a right triangle. In the 12th century, the post-classical Latin word ''orthogonalis'' came to mean a right angle or something related to a right angle. Mathematics Physics Optics In optics, polarization states are said to be ort ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |