|
Models Of Computation
In computer science, and more specifically in computability theory and computational complexity theory, a model of computation is a model which describes how an output of a mathematical function is computed given an input. A model describes how units of computations, memories, and communications are organized. The computational complexity of an algorithm can be measured given a model of computation. Using a model allows studying the performance of algorithms independently of the variations that are specific to particular implementations and specific technology. Categories Models of computation can be classified into three categories: sequential models, functional models, and concurrent models. Sequential models Sequential models include: * Finite-state machines * Post machines ( Post–Turing machines and tag machines). * Pushdown automata * Register machines ** Random-access machines * Turing machines * Decision tree model * External memory model Functional models Functio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Computer Science
Computer science is the study of computation, information, and automation. Computer science spans Theoretical computer science, theoretical disciplines (such as algorithms, theory of computation, and information theory) to Applied science, applied disciplines (including the design and implementation of Computer architecture, hardware and Software engineering, software). Algorithms and data structures are central to computer science. The theory of computation concerns abstract models of computation and general classes of computational problem, problems that can be solved using them. The fields of cryptography and computer security involve studying the means for secure communication and preventing security vulnerabilities. Computer graphics (computer science), Computer graphics and computational geometry address the generation of images. Programming language theory considers different ways to describe computational processes, and database theory concerns the management of re ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Combinatory Logic
Combinatory logic is a notation to eliminate the need for quantified variables in mathematical logic. It was introduced by Moses Schönfinkel and Haskell Curry, and has more recently been used in computer science as a theoretical model of computation and also as a basis for the design of functional programming languages. It is based on combinators, which were introduced by Schönfinkel in 1920 with the idea of providing an analogous way to build up functions—and to remove any mention of variables—particularly in predicate logic. A combinator is a higher-order function that uses only function application and earlier defined combinators to define a result from its arguments. In mathematics Combinatory logic was originally intended as a 'pre-logic' that would clarify the role of quantified variables in logic, essentially by eliminating them. Another way of eliminating quantified variables is Quine's predicate functor logic. While the expressive power of combinatory log ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nondeterministic Model Of Computation
In theoretical computer science, a nondeterministic Turing machine (NTM) is a theoretical model of computation whose governing rules specify more than one possible action when in some given situations. That is, an NTM's next state is ''not'' completely determined by its action and the current symbol it sees, unlike a deterministic Turing machine. NTMs are sometimes used in thought experiments to examine the abilities and limits of computers. One of the most important open problems in theoretical computer science is the P versus NP problem, which (among other equivalent formulations) concerns the question of how difficult it is to simulate nondeterministic computation with a deterministic computer. Background In essence, a Turing machine is imagined to be a simple computer that reads and writes symbols one at a time on an endless tape by strictly following a set of rules. It determines what action it should perform next according to its internal ''state'' and ''what symbol it cu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Deterministic Model
In mathematics, computer science and physics, a deterministic system is a system in which no randomness is involved in the development of future states of the system. A deterministic model will thus always produce the same output from a given starting condition or initial state. In physics Physical laws that are described by differential equations represent deterministic systems, even though the state of the system at a given point in time may be difficult to describe explicitly. In quantum mechanics, the Schrödinger equation, which describes the continuous time evolution of a system's wave function, is deterministic. However, the relationship between a system's wave function and the observable properties of the system appears to be non-deterministic. In mathematics The systems studied in chaos theory are deterministic. If the initial state were known exactly, then the future state of such a system could theoretically be predicted. However, in practice, knowledge about the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Synchronous Data Flow
Synchronous Data Flow (SDF) is a restriction on Kahn process networks where the number of tokens read and written by each process is known ahead of time. In some cases, processes can be scheduled such that channels have bounded FIFOs. Limitations SDF does not account for asynchronous processes as their token read/write rates will vary. Practically, one can divide the network into synchronous sub-networks connected by asynchronous links. Alternatively a runtime supervisor can enforce fairness and other desired properties. Applications SDF is useful for modeling digital signal processing (DSP) routines. Models can be compiled to target parallel hardware like FPGAs, processors with DSP instruction sets like Qualcomm's Hexagon, and other systems. See also * Kahn process networks * Petri net *Dataflow architecture Dataflow architecture is a dataflow-based computer architecture that directly contrasts the traditional von Neumann architecture or control flow architecture ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Process Calculus
In computer science, the process calculi (or process algebras) are a diverse family of related approaches for formally modelling concurrent systems. Process calculi provide a tool for the high-level description of interactions, communications, and synchronizations between a collection of independent agents or processes. They also provide algebraic laws that allow process descriptions to be manipulated and analyzed, and permit formal reasoning about equivalences between processes (e.g., using bisimulation). Leading examples of process calculi include CSP, CCS, ACP, and LOTOS. More recent additions to the family include the π-calculus, the ambient calculus, PEPA, the fusion calculus and the join-calculus. Essential features While the variety of existing process calculi is very large (including variants that incorporate stochastic behaviour, timing information, and specializations for studying molecular interactions), there are several features that all process calculi h ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
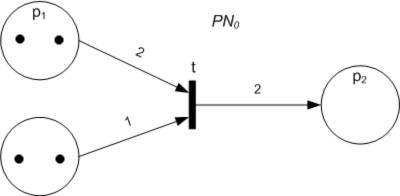
Petri Nets
A Petri net, also known as a place/transition net (PT net), is one of several mathematical modeling languages for the description of distributed systems. It is a class of discrete event dynamic system. A Petri net is a directed bipartite graph that has two types of elements: places and transitions. Place elements are depicted as white circles and transition elements are depicted as rectangles. A place can contain any number of tokens, depicted as black circles. A transition is enabled if all places connected to it as inputs contain at least one token. Some sources state that Petri nets were invented in August 1939 by Carl Adam Petri — at the age of 13 — for the purpose of describing chemical processes. Like industry standards such as UML activity diagrams, Business Process Model and Notation, and event-driven process chains, Petri nets offer a graphical notation for stepwise processes that include choice, iteration, and concurrent execution. Unlike these standards, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Circuit (computer Science)
In theoretical computer science, a circuit is a model of computation in which input values proceed through a sequence of gates, each of which computes a function. Circuits of this kind provide a generalization of Boolean circuits and a mathematical model for digital logic circuits. Circuits are defined by the gates they contain and the values the gates can produce. For example, the values in a Boolean circuit are Boolean values, and the circuit includes conjunction, disjunction, and negation gates. The values in an integer circuit are sets of integers and the gates compute set union, set intersection, and set complement, as well as the arithmetic operations addition and multiplication. Formal definition A circuit is a triplet (M, L, G), where * M is a set of values, * L is a set of gate labels, each of which is a function from M^ to M for some non-negative integer i (where i represents the number of inputs to the gate), and * G is a labelled graph, labelled directed acyclic gra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Logic Gate
A logic gate is a device that performs a Boolean function, a logical operation performed on one or more binary inputs that produces a single binary output. Depending on the context, the term may refer to an ideal logic gate, one that has, for instance, zero rise time and unlimited fan-out, or it may refer to a non-ideal physical device (see ideal and real op-amps for comparison). The primary way of building logic gates uses diodes or transistors acting as electronic switches. Today, most logic gates are made from MOSFETs (metal–oxide–semiconductor field-effect transistors). ''From Integrated circuit'' They can also be constructed using vacuum tubes, electromagnetic relays with relay logic, fluidic logic, pneumatic logic, optics, molecules, acoustics, or even mechanical or thermal elements. Logic gates can be cascaded in the same way that Boolean functions can be composed, allowing the construction of a physical model of all of Boolean logic, and therefore, all o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kahn Process Networks
A Kahn process network (KPN, or process network) is a Distributed computing, distributed ''model of computation'' in which a group of deterministic sequential Process (computing), processes communicate through unbounded FIFO (computing and electronics), first in, first out channels. The model requires that reading from a channel is Blocking (computing), blocking while writing is Asynchronous I/O, non-blocking. Due to these key restrictions, the resulting process network exhibits Deterministic algorithm, deterministic behavior that does not depend on the timing of computation nor on Network delay, communication delays. Kahn process networks were originally developed for modeling parallel programs, but have proven convenient for modeling embedded systems, high-performance computing systems, signal processing systems, stream processing systems, dataflow programming languages, and other computational tasks. KPNs were introduced by Gilles Kahn in 1974. Execution model KPN is a common m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |