|
Knot Theory
In topology, knot theory is the study of knot (mathematics), mathematical knots. While inspired by knots which appear in daily life, such as those in shoelaces and rope, a mathematical knot differs in that the ends are joined so it cannot be undone, the simplest knot being a ring (or "unknot"). In mathematical language, a knot is an embedding of a circle in 3-dimensional Euclidean space, \mathbb^3. Two mathematical knots are equivalent if one can be transformed into the other via a deformation of \mathbb^3 upon itself (known as an ambient isotopy); these transformations correspond to manipulations of a knotted string that do not involve cutting it or passing it through itself. Knots can be described in various ways. Using different description methods, there may be more than one description of the same knot. For example, a common method of describing a knot is a planar diagram called a knot diagram, in which any knot can be drawn in many different ways. Therefore, a fundamental p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tabela De Nós Matemáticos 01, Crop
''Durio graveolens,'' sometimes called the red-fleshed durian, orange-fleshed durian, or yellow durian, is a species of tree in the family Malvaceae. It is one of six species of durian named by Italian naturalist Odoardo Beccari. The specific epithet ('strong smelling' or 'rank') is due to the odor. Although most species of ''Durio'' (most notably ''Durio dulcis'') have a strong scent, the red-fleshed type of ''D. graveolens'' has a mild scent. It is native to Southeast Asia. ''D. graveolens'' is an edible durian, perhaps the most popular 'wild' species of durian, and it is sold commercially regionally. Description ''D. graveolens'' is a large tree, sharing many features with ''Durio dulcis, D. dulcis''. It inhabits the upper Canopy (biology), canopy, growing up to tall. The trunk is in diameter and can have no branches until about high. The trunk will be smooth or flaky, grey/mauve to ruddy brown with steep buttress roots. The buttresses reach and extend out . The oblong ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
3-manifold
In mathematics, a 3-manifold is a topological space that locally looks like a three-dimensional Euclidean space. A 3-manifold can be thought of as a possible shape of the universe. Just as a sphere looks like a plane (geometry), plane (a tangent plane) to a small and close enough observer, all 3-manifolds look like our universe does to a small enough observer. This is made more precise in the definition below. Principles Definition A topological space M is a 3-manifold if it is a second-countable Hausdorff space and if every point in M has a neighbourhood (mathematics), neighbourhood that is homeomorphic to Euclidean 3-space. Mathematical theory of 3-manifolds The topological, Piecewise linear manifold, piecewise-linear, and smooth categories are all equivalent in three dimensions, so little distinction is made in whether we are dealing with say, topological 3-manifolds, or smooth 3-manifolds. Phenomena in three dimensions can be strikingly different from phenomena in other dim ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Alexandre-Théophile Vandermonde
Alexandre-Théophile Vandermonde (28 February 1735 – 1 January 1796) was a French mathematician, musician, and chemist who worked with Bézout and Lavoisier; his name is now principally associated with determinant theory in mathematics. He was born in Paris, and died there. Biography Vandermonde was a violinist, and became engaged with mathematics only around 1770. In ''Mémoire sur la résolution des équations'' (1771) he reported on symmetric functions and solution of cyclotomic polynomials; this paper anticipated later Galois theory (see also abstract algebra for the role of Vandermonde in the genesis of group theory). In ''Remarques sur des problèmes de situation'' (1771) he studied knight's tours, and presaged the development of knot theory by explicitly noting the importance of topological features when discussing the properties of knots: ''"Whatever the twists and turns of a system of threads in space, one can always obtain an expression for the calculation of its dim ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Peter Guthrie Tait
Peter Guthrie Tait (28 April 18314 July 1901) was a Scottish Mathematical physics, mathematical physicist and early pioneer in thermodynamics. He is best known for the mathematical physics textbook ''Treatise on Natural Philosophy'', which he co-wrote with William Thomson, 1st Baron Kelvin, Lord Kelvin, and his early investigations into knot theory. His work on knot theory contributed to the eventual formation of topology as a mathematical discipline. His name is known in graph theory mainly for Tait's conjecture on cubic graphs. He is also one of the namesakes of the Tait–Kneser theorem on osculating circles. Early life Tait was born in Dalkeith on 28 April 1831 the only son of Mary Ronaldson and John Tait, secretary to the Walter Montagu Douglas Scott, 5th Duke of Buccleuch, 5th Duke of Buccleuch. He was educated at Dalkeith Grammar School then Edinburgh Academy, where he began his lifelong friendship with James Clerk Maxwell. He studied mathematics and physics at the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Celtic Knot
Celtic knots (, , , ) are a variety of knots and Style (visual arts)#Stylization, stylized graphical representations of knots used for decoration, used extensively in the Celtic style of Insular art. These knots are most known for their adaptation for use in the ornament (architecture), ornamentation of Christian monuments and manuscripts, such as the 8th-century St. Teilo Gospels, the Book of Kells and the Lindisfarne Gospels. Most are endless knots, and many are varieties of basket weave knots. History The use of interlace (visual arts), interlace patterns had its origins in the late Roman Empire. Knot patterns first appeared in the third and fourth centuries AD and can be seen in Roman floor mosaics of that time. Interesting developments in the artistic use of interlaced knot patterns are found in Byzantine architecture and Illuminated manuscript, book illumination, Coptic art, Celtic art, Islamic art, Kievan Rus' book illumination, Ethiopian art, and European architecture ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Book Of Kells
The Book of Kells (; ; Dublin, Trinity College Library, MS A. I. [58], sometimes known as the Book of Columba) is an illustrated manuscript and Celts, Celtic Gospel book in Latin, containing the Gospel, four Gospels of the New Testament together with various prefatory texts and tables. It was created in a Columban monastery in either Ireland or Scotland, and may have had contributions from various Columban institutions from each of these areas. It is believed to have been created 800 AD. The text of the Gospels is largely drawn from the Vulgate, although it also includes several passages drawn from the earlier versions of the Bible known as the ''Vetus Latina''. It is regarded as a masterwork of Western calligraphy and the pinnacle of Insular art, Insular illumination. The manuscript takes its name from the Abbey of Kells, County Meath, which was its home for centuries. The illustrations and ornamentation of the Book of Kells surpass those of other Insular Gospel books in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Celtic Christianity
Celtic Christianity is a form of Christianity that was common, or held to be common, across the Celtic languages, Celtic-speaking world during the Early Middle Ages. The term Celtic Church is deprecated by many historians as it implies a unified and identifiable entity entirely separate from that of mainstream Western Christendom. For this reason, many prefer the term Insular Christianity. As Patrick Wormald explained, "One of the common misconceptions is that there was a ''Roman'' Church to which the ''Celtic'' Church was nationally opposed." Some writers have described a distinct "Celtic Church" uniting the Celts (modern), Celtic peoples and distinguishing them from adherents of the Latin Church, Roman Church, while others classify Celtic Christianity as a set of distinctive practices occurring in those areas. Varying scholars reject the former notion, but note that there were certain traditions and practices present in both the Irish and British churches that were not seen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Borromean Rings
In mathematics, the Borromean rings are three simple closed curves in three-dimensional space that are link (knot theory), topologically linked and cannot be separated from each other, but that break apart into two unknotted and unlinked loops when any one of the three is cut or removed. Most commonly, these rings are drawn as three circles in the plane, in the pattern of a Venn diagram, alternating link, alternatingly crossing over and under each other at the points where they cross. Other triples of curves are said to form the Borromean rings as long as they are topologically equivalent to the curves depicted in this drawing. The Borromean rings are named after the Italian House of Borromeo, who used the circular form of these rings as an element of their coat of arms, but designs based on the Borromean rings have been used in many cultures, including by the Norsemen and in Japan. They have been used in Christian symbolism as a sign of the Trinity, and in modern commerce as the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tibetan Buddhism
Tibetan Buddhism is a form of Buddhism practiced in Tibet, Bhutan and Mongolia. It also has a sizable number of adherents in the areas surrounding the Himalayas, including the Indian regions of Ladakh, Gorkhaland Territorial Administration, Darjeeling, Sikkim, and Arunachal Pradesh, as well as in Nepal. Smaller groups of practitioners can be found in Central Asia, some regions of China such as Northeast China, Xinjiang, Inner Mongolia and some regions of Russia, such as Tuva, Buryatia, and Kalmykia. Tibetan Buddhism evolved as a form of Mahayana, Mahāyāna Buddhism stemming from the latest stages of Indian Buddhism (which included many Vajrayana, Vajrayāna elements). It thus preserves many Indian Buddhist Tantra, tantric practices of the Gupta Empire, post-Gupta Medieval India, early medieval period (500–1200 CE), along with numerous native Tibetan developments. In the pre-modern era, Tibetan Buddhism spread outside of Tibet primarily due to the influence of the Mongol Emp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Endless Knot
file:Endless knot detail, from- Burmese-Pali Manuscript. Wellcome L0026495 (cropped).jpg, Endless knot in a Burmese Pali manuscript The endless knot or eternal knot is a symbolic Knot (mathematics), knot and one of the Ashtamangala, Eight Auspicious Symbols. It is an important symbol in Hinduism, Jainism and Buddhism. It is an important cultural marker in places significantly influenced by Tibetan Buddhism such as Tibet, Mongolia, Tuva, Kalmykia, and Buryatia. It is also found in Celtic knot, Celtic, Kazakh culture, Kazakh and Chinese knotting, Chinese symbolism. History The endless knot appears on clay tablets from the Indus Valley civilization (2500 BC) and on a historic era inscription. While associated with Dharmic religions, it also appears in Islamic art. It likely was introduced due to trade and other cultural contact with China, the Mongols, and Iran. Interpretations Buddhism Various Buddhist interpretations of the symbol are: * The endless knot iconography sym ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chinese Knotting
Chinese knotting, also known as (), is a Chinese folk art with ties to Buddhism and Taoism. A Chinese knot is made from a single length of cord that is woven into different shapes, with each shape having a symbolic meaning. The most common color used in Chinese knotting is red, a color Color in Chinese culture, associated with luck in Chinese culture, although any color can be used. Charms, beads, and jade are sometimes incorporated into a Chinese knot. It is believed that Chinese knotting originated for recording information and exchanging messages before writing was commonplace. Traditionally, Chinese knots acted as good-luck charms to ward off evil spirits. Chinese knots are used today to decorate homes during festivities and are also commonly seen in traditional jade jewellery and Chinese clothing, traditional Chinese clothing. Characteristics Chinese knots come in a variety of shapes and sizes. They are made from a single cord and are often double-layered and Symmetry, sy ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
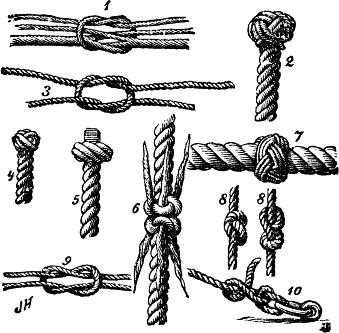
Knot Tying
A knot is an intentional complication in cordage which may be practical or decorative, or both. Practical knots are classified by function, including hitches, bends, loop knots, and splices: a ''hitch'' fastens a rope to another object; a ''bend'' fastens two ends of a rope to each another; a ''loop knot'' is any knot creating a loop; and ''splice'' denotes any multi-strand knot, including bends and loops. A knot may also refer, in the strictest sense, to a stopper or knob at the end of a rope to keep that end from slipping through a grommet or eye. Knots have excited interest since ancient times for their practical uses, as well as their topological intricacy, studied in the area of mathematics known as knot theory. History Knots and knotting have been used and studied throughout history. For example, Chinese knotting is a decorative handicraft art that began as a form of Chinese folk art in the Tang and Song Dynasty (960–1279 AD) in China, later popularized in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |