|
Isohedral Tilings
In geometry, a tessellation of dimension (a plane tiling) or higher, or a polytope of dimension (a polyhedron) or higher, is isohedral or face-transitive if all its faces are the same. More specifically, all faces must be not merely congruent but must be ''transitive'', i.e. must lie within the same '' symmetry orbit''. In other words, for any two faces and , there must be a symmetry of the ''entire'' figure by translations, rotations, and/or reflections that maps onto . For this reason, convex isohedral polyhedra are the shapes that will make fair dice. Isohedral polyhedra are called isohedra. They can be described by their face configuration. An isohedron has an even number of faces. The dual of an isohedral polyhedron is vertex-transitive, i.e. isogonal. The Catalan solids, the bipyramids, and the trapezohedra are all isohedral. They are the duals of the (isogonal) Archimedean solids, prisms, and antiprisms, respectively. The Platonic solids, which are eith ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dice Set
A die (: dice, sometimes also used as ) is a small, throwable object with marked sides that can rest in multiple positions. Dice are used for generating Statistical randomness, random values, commonly as part of tabletop games, including List of dice games, dice games, board games, role-playing games, and Game of chance, games of chance. A traditional die is a cube with each of its six faces marked with a different number of dots (pip (counting), pips) from one to six. When thrown or rolled, the die comes to rest showing a random integer from one to six on its upper surface, with each value being equally likely. Dice may also have other polyhedron, polyhedral or irregular shapes, may have faces marked with numerals or symbols instead of pips and may have their numbers carved out from the material of the dice instead of marked on it. Loaded dice are specifically designed or modified to favor some results over others, for cheating or entertainment purposes. History Dice have bee ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Catalan Solids
The Catalan solids are the dual polyhedra of Archimedean solids. The Archimedean solids are thirteen highly-symmetric polyhedra with regular faces and symmetric vertices. The faces of the Catalan solids correspond by duality to the vertices of Archimedean solids, and vice versa. One way to construct the Catalan solids is by using the Dorman Luke construction. The Catalan solids are face-transitive or ''isohedral'' meaning that their faces are symmetric to one another, but they are not vertex-transitive because their vertices are not symmetric. Their dual, the Archimedean solids, are vertex-transitive but not face-transitive. Each Catalan solid has constant dihedral angles, meaning the angle between any two adjacent faces is the same. Additionally, two Catalan solids, the rhombic dodecahedron and rhombic triacontahedron, are edge-transitive, meaning their edges are symmetric to each other. Some Catalan solids were discovered by Johannes Kepler during his study of zonohedra, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Regular Polyhedron
A regular polyhedron is a polyhedron whose symmetry group acts transitive group action, transitively on its Flag (geometry), flags. A regular polyhedron is highly symmetrical, being all of edge-transitive, vertex-transitive and face-transitive. In classical contexts, many different equivalent definitions are used; a common one is that the faces are Congruence (geometry), congruent regular polygons which are assembled in the same way around each vertex (geometry), vertex. A regular polyhedron is identified by its Schläfli symbol of the form , where ''n'' is the number of sides of each face and ''m'' the number of faces meeting at each vertex. There are 5 finite convex regular polyhedra (the Platonic solids), and four regular star polyhedra (the Kepler–Poinsot polyhedra), making nine regular polyhedra in all. In addition, there are five regular compounds of the regular polyhedra. The regular polyhedra There are five Convex polygon, convex regular polyhedra, known as the Platoni ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hexagonal Bipyramid
A hexagonal bipyramid is a polyhedron formed from two hexagonal pyramids joined at their bases. The resulting solid has 12 triangular faces, 8 vertices and 18 edges. The 12 faces are identical isosceles triangles. Although it is face-transitive, it is not a Platonic solid because some vertices have four faces meeting and others have six faces, and it is not a Johnson solid because its faces cannot be equilateral triangles; 6 equilateral triangles would make a flat vertex. It is one of an infinite set of bipyramids. Having twelve faces, it is a type of dodecahedron, although that name is usually associated with the regular polyhedral form with pentagonal faces. The hexagonal bipyramid has a plane of symmetry (which is horizontal in the figure to the right) where the bases of the two pyramids are joined. This plane is a regular hexagon. There are also six planes of symmetry crossing through the two apices. These planes are rhombic and lie at 30° angles to each other, perp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rhombic Icosahedron
The rhombic icosahedron is a polyhedron shaped like an Oblate spheroid, oblate sphere. Its 20 faces are Congruence (geometry), congruent golden rhombi; 3, 4, or 5 faces meet at each vertex. It has 5 faces (green on top figure) meeting at each of its 2 poles; these 2 vertices lie on its axis of 5-fold symmetry, which is perpendicular to 5 axes of 2-fold symmetry through the midpoints of opposite equatorial edges (example on top figure: most left-hand and most right-hand mid-edges). Its other 10 faces follow its equator, 5 above and 5 below it; each of these 10 rhombi has 2 of its 4 sides lying on this zig-zag Skew polygon, skew decagon equator. The rhombic icosahedron has 22 vertices. It has Dihedral symmetry in three dimensions, D5d, [2+,10], (2*5) symmetry group, of order 20; thus it has a center of symmetry (since 5 is odd). Even though all its faces are congruent, the rhombic icosahedron is not face-transitive, since one can distinguish whether a particular face is near the eq ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Noble Polyhedron
A noble polyhedron is one which is isohedral (all faces the same) and isogonal (all vertices the same). They were first studied in any depth by Edmund Hess and Max Brückner in the late 19th century, and later by Branko Grünbaum. Classes of noble polyhedra There are several main classes of noble polyhedra: * Regular polyhedra, that is, the five Platonic solids and the four Kepler–Poinsot polyhedra. * Disphenoid tetrahedra. * Crown polyhedra, also known as stephanoid polyhedra. * A variety of miscellaneous examples, e.g. the stellated icosahedra D and H, or their duals. It is not known whether there are finitely many, and if so how many might remain to be discovered. If we allow some of Grünbaum's stranger constructions as polyhedra, then we have two more infinite series of toroids (besides the crown polyhedra mentioned above): * Wreath polyhedra. These have triangular faces in coplanar pairs which share an edge. * V-faced polyhedra. These have vertices in coincident pa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quasiregular Polyhedron
In geometry, a quasiregular polyhedron is a uniform polyhedron that has exactly two kinds of regular faces, which alternate around each vertex. They are vertex-transitive and edge-transitive, hence a step closer to regular polyhedra than the semiregular, which are merely vertex-transitive. Their dual figures are face-transitive and edge-transitive; they have exactly two kinds of regular vertex figures, which alternate around each face. They are sometimes also considered quasiregular. There are only two convex quasiregular polyhedra: the cuboctahedron and the icosidodecahedron. Their names, given by Kepler, come from recognizing that their faces are all the faces (turned differently) of the dual-pair cube and octahedron, in the first case, and of the dual-pair icosahedron and dodecahedron, in the second case. These forms representing a pair of a regular figure and its dual can be given a vertical Schläfli symbol \begin p \\ q \end or ''r'', to represent that their ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Edge-transitive
In geometry, a polytope (for example, a polygon or a polyhedron) or a Tessellation, tiling is isotoxal () or edge-transitive if its Symmetry, symmetries act Transitive group action, transitively on its Edge (geometry), edges. Informally, this means that there is only one type of edge to the object: given two edges, there is a Translation (geometry), translation, Rotation (mathematics), rotation, and/or Reflection (mathematics), reflection that will move one edge to the other while leaving the region occupied by the object unchanged. Isotoxal polygons An isotoxal polygon is an even-sided i.e. equilateral polygon, but not all equilateral polygons are isotoxal. The Duality (mathematics)#Dimension-reversing dualities, duals of isotoxal polygons are isogonal polygons. Isotoxal 4n-gons are Central symmetry, centrally symmetric, thus are also zonogons. In general, a (non-regular) isotoxal 2n-gon has \mathrm_n, (^*nn) dihedral symmetry. For example, a (non-square) rhombus is an isotoxa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Platonic Solids
In geometry, a Platonic solid is a convex, regular polyhedron in three-dimensional Euclidean space. Being a regular polyhedron means that the faces are congruent (identical in shape and size) regular polygons (all angles congruent and all edges congruent), and the same number of faces meet at each vertex. There are only five such polyhedra: Geometers have studied the Platonic solids for thousands of years. They are named for the ancient Greek philosopher Plato, who hypothesized in one of his dialogues, the '' Timaeus'', that the classical elements were made of these regular solids. History The Platonic solids have been known since antiquity. It has been suggested that certain carved stone balls created by the late Neolithic people of Scotland represent these shapes; however, these balls have rounded knobs rather than being polyhedral, the numbers of knobs frequently differed from the numbers of vertices of the Platonic solids, there is no ball whose knobs match the 20 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
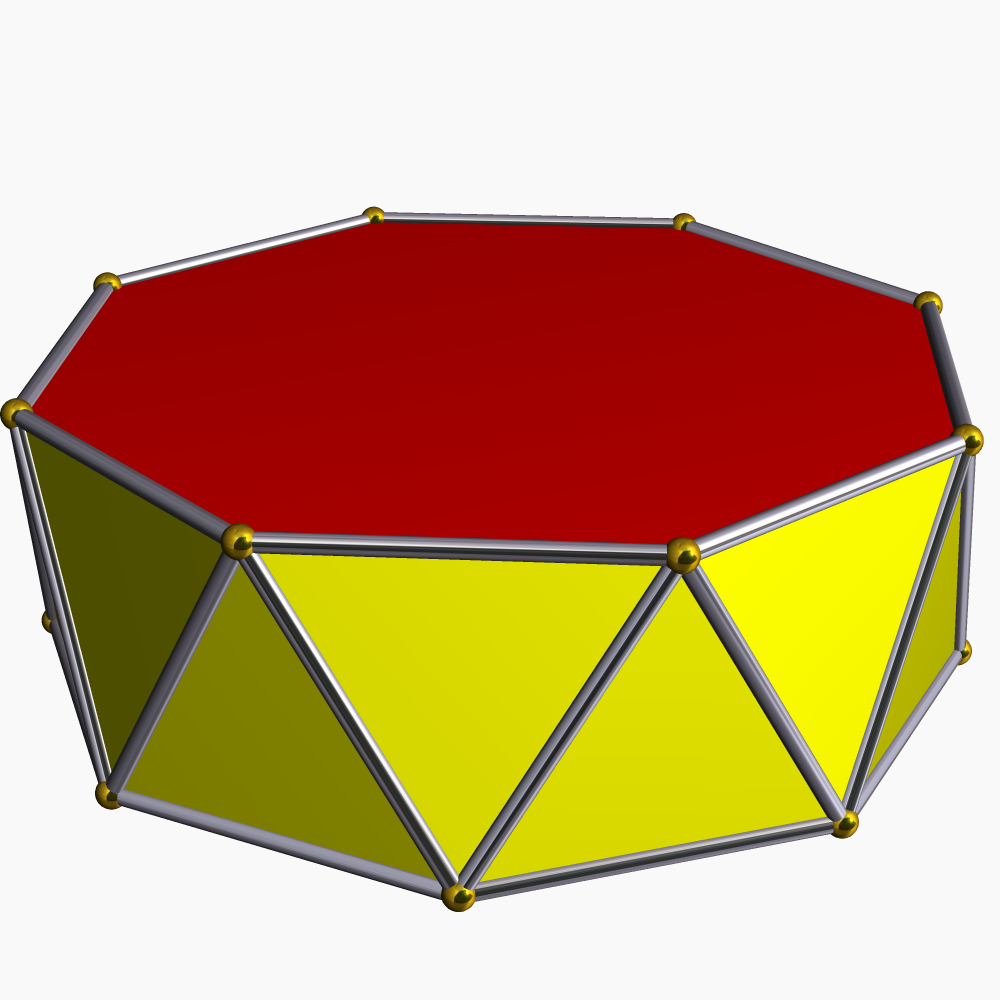
Antiprism
In geometry, an antiprism or is a polyhedron composed of two Parallel (geometry), parallel Euclidean group, direct copies (not mirror images) of an polygon, connected by an alternating band of triangles. They are represented by the Conway polyhedron notation, Conway notation . Antiprisms are a subclass of prismatoids, and are a (degenerate) type of snub polyhedron. Antiprisms are similar to Prism (geometry), prisms, except that the bases are twisted relatively to each other, and that the side faces (connecting the bases) are triangles, rather than quadrilaterals. The dual polyhedron of an -gonal antiprism is an -gonal trapezohedron. History In his 1619 book ''Harmonices Mundi'', Johannes Kepler observed the existence of the infinite family of antiprisms. This has conventionally been thought of as the first discovery of these shapes, but they may have been known earlier: an unsigned printing block for the net (geometry), net of a hexagonal antiprism has been attributed ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prism (geometry)
In geometry, a prism is a polyhedron comprising an polygon Base (geometry), base, a second base which is a Translation (geometry), translated copy (rigidly moved without rotation) of the first, and other Face (geometry), faces, necessarily all parallelograms, joining corresponding sides of the two bases. All Cross section (geometry), cross-sections parallel to the bases are translations of the bases. Prisms are named after their bases, e.g. a prism with a pentagonal base is called a pentagonal prism. Prisms are a subclass of prismatoids. Like many basic geometric terms, the word ''prism'' () was first used in Euclid's Elements, Euclid's ''Elements''. Euclid defined the term in Book XI as "a solid figure contained by two opposite, equal and parallel planes, while the rest are parallelograms". However, this definition has been criticized for not being specific enough in regard to the nature of the bases (a cause of some confusion amongst generations of later geometry writers). ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |