|
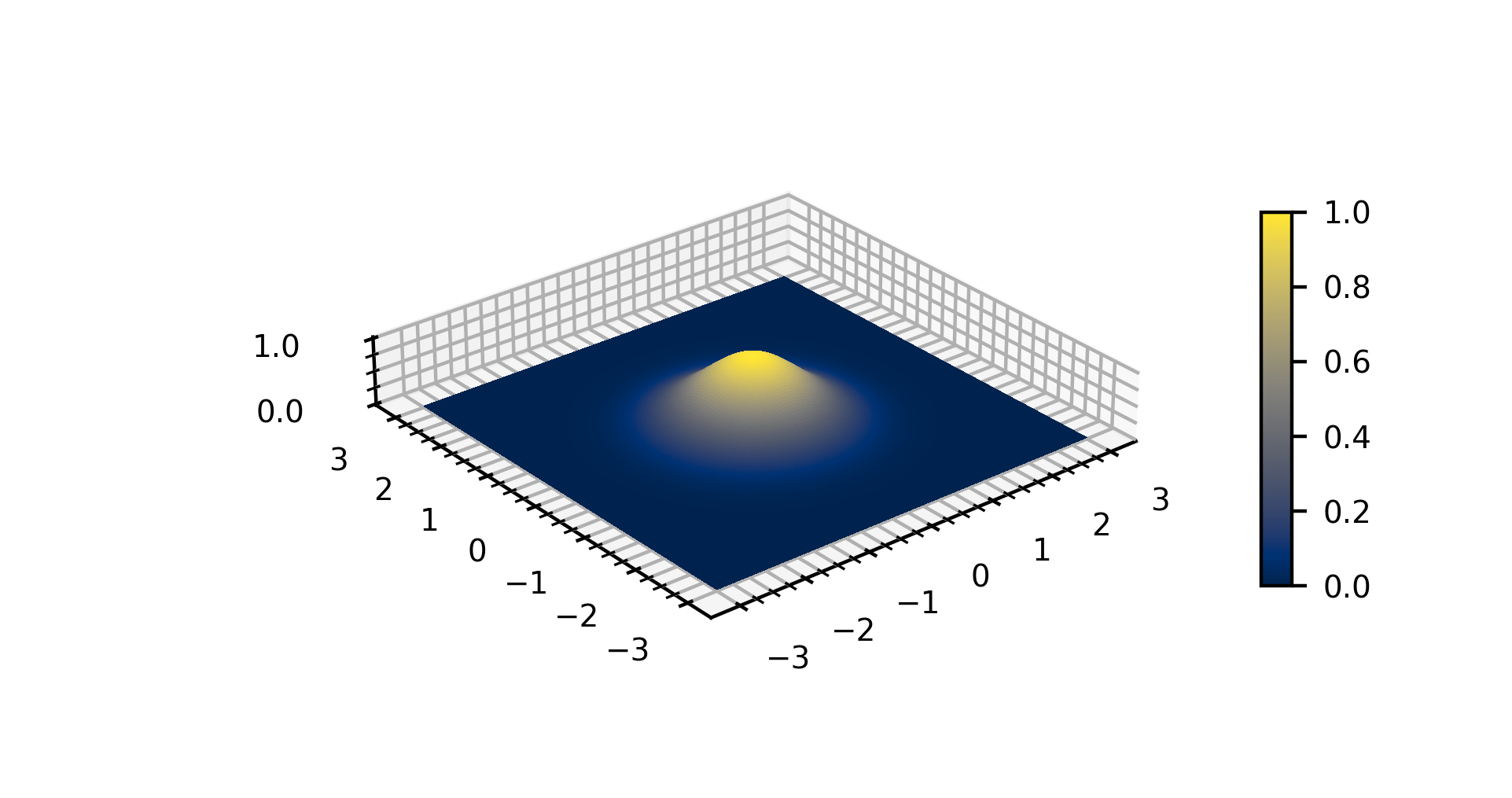
Crystal Ball Function
The Crystal Ball function, named after the Crystal Ball Collaboration (hence the capitalized initial letters), is a probability density function (PDF) commonly used to model various lossy processes in high-energy physics such as Bremsstrahlung by electrons. It consists of a Gaussian core portion and a power-law low-end tail, below a certain threshold. The function itself and its first derivative are both continuous. The Crystal Ball function is given by: :f(x;\alpha,n,\bar x,\sigma) = N \cdot \begin \exp(- \frac), & \mbox\frac > -\alpha \\ A \cdot (B - \frac)^, & \mbox\frac \leqslant -\alpha \end , where :A = \left(\frac\right)^n \cdot \exp\left(- \frac \right), :B = \frac - \left, \alpha \, :N = \frac, :C = \frac \cdot \frac \cdot \exp\left(- \frac \right), :D = \sqrt \left(1 + \operatorname\left(\frac\right)\right), with the error function erf. The parameters of the function (that are usually determined by a fit) are: * N is a normalization factor (Skwarnicki 1986) * \alp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Crystal Ball (detector)
The Crystal Ball was a hermetic particle detector used initially with the SPEAR particle accelerator at the Stanford Linear Accelerator Center beginning in 1979. It was designed to detect neutral particles and was used to discover the ηc meson. Its central section was a spark chamber surrounded by a nearly-complete sphere of scintillating crystals ( NaI(Tl)), for which it was named. With the addition of endcaps of similar construction, the detector covered 98% of the solid angle around the interaction point. After its decommissioning at SLAC, the detector was carried to DESY, where it was used for b-physics experiments. In 1996, it was moved to the Alternating Gradient Synchrotron (AGS) at Brookhaven National Laboratory, where it was used in a series of pion- and kaon-induced experiments on the proton. Currently it is located at Mainz Microtron facility, where it is being used by the A2 Collaboration for a diverse program of measurements using energy tagged Bremsstrahlung p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probability Density Function
In probability theory, a probability density function (PDF), density function, or density of an absolutely continuous random variable, is a Function (mathematics), function whose value at any given sample (or point) in the sample space (the set of possible values taken by the random variable) can be interpreted as providing a ''relative likelihood'' that the value of the random variable would be equal to that sample. Probability density is the probability per unit length, in other words, while the ''absolute likelihood'' for a continuous random variable to take on any particular value is 0 (since there is an infinite set of possible values to begin with), the value of the PDF at two different samples can be used to infer, in any particular draw of the random variable, how much more likely it is that the random variable would be close to one sample compared to the other sample. More precisely, the PDF is used to specify the probability of the random variable falling ''within ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
High-energy Physics
Particle physics or high-energy physics is the study of fundamental particles and forces that constitute matter and radiation. The field also studies combinations of elementary particles up to the scale of protons and neutrons, while the study of combinations of protons and neutrons is called nuclear physics. The fundamental particles in the universe are classified in the Standard Model as fermions (matter particles) and bosons (force-carrying particles). There are three generations of fermions, although ordinary matter is made only from the first fermion generation. The first generation consists of up and down quarks which form protons and neutrons, and electrons and electron neutrinos. The three fundamental interactions known to be mediated by bosons are electromagnetism, the weak interaction, and the strong interaction. Quarks cannot exist on their own but form hadrons. Hadrons that contain an odd number of quarks are called baryons and those that contain an even numbe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bremsstrahlung
In particle physics, bremsstrahlung (; ; ) is electromagnetic radiation produced by the deceleration of a charged particle when deflected by another charged particle, typically an electron by an atomic nucleus. The moving particle loses kinetic energy, which is converted into radiation (i.e., photons), thus satisfying the law of conservation of energy. The term is also used to refer to the process of producing the radiation. Bremsstrahlung has a continuous spectrum, which becomes more intense and whose peak intensity shifts toward higher frequencies as the change of the energy of the decelerated particles increases. Broadly speaking, bremsstrahlung or braking radiation is any radiation produced due to the acceleration (positive or negative) of a charged particle, which includes synchrotron radiation (i.e., photon emission by a relativistic particle), cyclotron radiation (i.e. photon emission by a non-relativistic particle), and the emission of electrons and positrons during ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gaussian Function
In mathematics, a Gaussian function, often simply referred to as a Gaussian, is a function (mathematics), function of the base form f(x) = \exp (-x^2) and with parametric extension f(x) = a \exp\left( -\frac \right) for arbitrary real number, real constants , and non-zero . It is named after the mathematician Carl Friedrich Gauss. The graph of a function, graph of a Gaussian is a characteristic symmetric "Normal distribution, bell curve" shape. The parameter is the height of the curve's peak, is the position of the center of the peak, and (the standard deviation, sometimes called the Gaussian Root mean square, RMS width) controls the width of the "bell". Gaussian functions are often used to represent the probability density function of a normal distribution, normally distributed random variable with expected value and variance . In this case, the Gaussian is of the form g(x) = \frac \exp\left( -\frac \frac \right). Gaussian functions are widely used in statistics to describ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Power-law
In statistics, a power law is a functional relationship between two quantities, where a relative change in one quantity results in a relative change in the other quantity proportional to the change raised to a constant exponent: one quantity varies as a power of another. The change is independent of the initial size of those quantities. For instance, the area of a square has a power law relationship with the length of its side, since if the length is doubled, the area is multiplied by 2, while if the length is tripled, the area is multiplied by 3, and so on. Empirical examples The distributions of a wide variety of physical, biological, and human-made phenomena approximately follow a power law over a wide range of magnitudes: these include the sizes of craters on the moon and of solar flares, cloud sizes, the foraging pattern of various species, the sizes of activity patterns of neuronal populations, the frequencies of words in most languages, frequencies of family names, the s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Derivative
In mathematics, the derivative is a fundamental tool that quantifies the sensitivity to change of a function's output with respect to its input. The derivative of a function of a single variable at a chosen input value, when it exists, is the slope of the tangent line to the graph of the function at that point. The tangent line is the best linear approximation of the function near that input value. For this reason, the derivative is often described as the instantaneous rate of change, the ratio of the instantaneous change in the dependent variable to that of the independent variable. The process of finding a derivative is called differentiation. There are multiple different notations for differentiation. '' Leibniz notation'', named after Gottfried Wilhelm Leibniz, is represented as the ratio of two differentials, whereas ''prime notation'' is written by adding a prime mark. Higher order notations represent repeated differentiation, and they are usually denoted in Leib ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Continuous Function
In mathematics, a continuous function is a function such that a small variation of the argument induces a small variation of the value of the function. This implies there are no abrupt changes in value, known as '' discontinuities''. More precisely, a function is continuous if arbitrarily small changes in its value can be assured by restricting to sufficiently small changes of its argument. A discontinuous function is a function that is . Until the 19th century, mathematicians largely relied on intuitive notions of continuity and considered only continuous functions. The epsilon–delta definition of a limit was introduced to formalize the definition of continuity. Continuity is one of the core concepts of calculus and mathematical analysis, where arguments and values of functions are real and complex numbers. The concept has been generalized to functions between metric spaces and between topological spaces. The latter are the most general continuous functions, and their d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Error Function
In mathematics, the error function (also called the Gauss error function), often denoted by , is a function \mathrm: \mathbb \to \mathbb defined as: \operatorname z = \frac\int_0^z e^\,\mathrm dt. The integral here is a complex Contour integration, contour integral which is path-independent because \exp(-t^2) is Holomorphic function, holomorphic on the whole complex plane \mathbb. In many applications, the function argument is a real number, in which case the function value is also real. In some old texts, the error function is defined without the factor of \frac. This nonelementary integral is a sigmoid function, sigmoid function that occurs often in probability, statistics, and partial differential equations. In statistics, for non-negative real values of , the error function has the following interpretation: for a real random variable that is normal distribution, normally distributed with mean 0 and standard deviation \frac, is the probability that falls in the range . ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mean
A mean is a quantity representing the "center" of a collection of numbers and is intermediate to the extreme values of the set of numbers. There are several kinds of means (or "measures of central tendency") in mathematics, especially in statistics. Each attempts to summarize or typify a given group of data, illustrating the magnitude and sign of the data set. Which of these measures is most illuminating depends on what is being measured, and on context and purpose. The ''arithmetic mean'', also known as "arithmetic average", is the sum of the values divided by the number of values. The arithmetic mean of a set of numbers ''x''1, ''x''2, ..., x''n'' is typically denoted using an overhead bar, \bar. If the numbers are from observing a sample of a larger group, the arithmetic mean is termed the '' sample mean'' (\bar) to distinguish it from the group mean (or expected value) of the underlying distribution, denoted \mu or \mu_x. Outside probability and statistics, a wide rang ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Standard Deviation
In statistics, the standard deviation is a measure of the amount of variation of the values of a variable about its Expected value, mean. A low standard Deviation (statistics), deviation indicates that the values tend to be close to the mean (also called the expected value) of the set, while a high standard deviation indicates that the values are spread out over a wider range. The standard deviation is commonly used in the determination of what constitutes an outlier and what does not. Standard deviation may be abbreviated SD or std dev, and is most commonly represented in mathematical texts and equations by the lowercase Greek alphabet, Greek letter Sigma, σ (sigma), for the population standard deviation, or the Latin script, Latin letter ''s'', for the sample standard deviation. The standard deviation of a random variable, Sample (statistics), sample, statistical population, data set, or probability distribution is the square root of its variance. (For a finite population, v ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |