|
Concordance Correlation Coefficient
In statistics, the concordance correlation coefficient measures the agreement between two variables, e.g., to evaluate reproducibility or for inter-rater reliability. Definition The form of the concordance correlation coefficient \rho_c as :\rho_c = \frac, where \mu_x and \mu_y are the means for the two variables and \sigma^2_x and \sigma^2_y are the corresponding variances. \rho is the Pearson's correlation coefficient between the two variables. This follows from its definition as :\rho_c = 1 - \frac . When the concordance correlation coefficient is computed on a N-length data set (i.e., N paired data values (x_n, y_n), for n=1,...,N), the form is :\hat_c = \frac, where the mean is computed as :\bar = \frac \sum_^N x_n and the variance :s_x^2 = \frac \sum_^N (x_n - \bar)^2 and the covariance :s_ = \frac \sum_^N (x_n - \bar)(y_n - \bar) . Whereas the ordinary correlation coefficient (Pearson's) is immune to whether the biased or unbiased versions for estimation of the variance i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Statistics
Statistics (from German language, German: ', "description of a State (polity), state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of statistical survey, surveys and experimental design, experiments. When census data (comprising every member of the target population) cannot be collected, statisticians collect data by developing specific experiment designs and survey sample (statistics), samples. Representative sampling assures that inferences and conclusions can reasonably extend from the sample ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Reproducibility
Reproducibility, closely related to replicability and repeatability, is a major principle underpinning the scientific method. For the findings of a study to be reproducible means that results obtained by an experiment or an observational study or in a statistical analysis of a data set should be achieved again with a high degree of reliability when the study is replicated. There are different kinds of replication but typically replication studies involve different researchers using the same methodology. Only after one or several such successful replications should a result be recognized as scientific knowledge. History The first to stress the importance of reproducibility in science was the Anglo-Irish chemist Robert Boyle, in England in the 17th century. Boyle's air pump was designed to generate and study vacuum, which at the time was a very controversial concept. Indeed, distinguished philosophers such as René Descartes and Thomas Hobbes denied the very possibility of vacuum ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
 |
Inter-rater Reliability
In statistics, inter-rater reliability (also called by various similar names, such as inter-rater agreement, inter-rater concordance, inter-observer reliability, inter-coder reliability, and so on) is the degree of agreement among independent observers who rate, code, or assess the same phenomenon. Assessment tools that rely on ratings must exhibit good inter-rater reliability, otherwise they are not test validity, valid tests. There are a number of statistics that can be used to determine inter-rater reliability. Different statistics are appropriate for different types of measurement. Some options are joint-probability of agreement, such as Cohen's kappa, Scott's pi and Fleiss' kappa; or inter-rater correlation, concordance correlation coefficient, intra-class correlation, and Krippendorff's alpha. Concept There are several operational definitions of "inter-rater reliability," reflecting different viewpoints about what is a reliable agreement between raters. There are three oper ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Biometrics (journal)
''Biometrics'' is a journal that publishes articles on the application of statistics and mathematics to the biological sciences. It is published by the International Biometric Society (IBS).Biometrics homepage Originally published in 1945 under the title ''Biometrics Bulletin'', the journal adopted the shorter title in 1947. Biometrics, Vol. 3, No. 1, Mar., 1947 Page 53 /ref> A notable contributor to the journal was R.A. Fisher, for whom a memorial edition was published in 1964. [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Mean
A mean is a quantity representing the "center" of a collection of numbers and is intermediate to the extreme values of the set of numbers. There are several kinds of means (or "measures of central tendency") in mathematics, especially in statistics. Each attempts to summarize or typify a given group of data, illustrating the magnitude and sign of the data set. Which of these measures is most illuminating depends on what is being measured, and on context and purpose. The ''arithmetic mean'', also known as "arithmetic average", is the sum of the values divided by the number of values. The arithmetic mean of a set of numbers ''x''1, ''x''2, ..., x''n'' is typically denoted using an overhead bar, \bar. If the numbers are from observing a sample of a larger group, the arithmetic mean is termed the '' sample mean'' (\bar) to distinguish it from the group mean (or expected value) of the underlying distribution, denoted \mu or \mu_x. Outside probability and statistics, a wide rang ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Variance
In probability theory and statistics, variance is the expected value of the squared deviation from the mean of a random variable. The standard deviation (SD) is obtained as the square root of the variance. Variance is a measure of dispersion, meaning it is a measure of how far a set of numbers is spread out from their average value. It is the second central moment of a distribution, and the covariance of the random variable with itself, and it is often represented by \sigma^2, s^2, \operatorname(X), V(X), or \mathbb(X). An advantage of variance as a measure of dispersion is that it is more amenable to algebraic manipulation than other measures of dispersion such as the expected absolute deviation; for example, the variance of a sum of uncorrelated random variables is equal to the sum of their variances. A disadvantage of the variance for practical applications is that, unlike the standard deviation, its units differ from the random variable, which is why the standard devi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
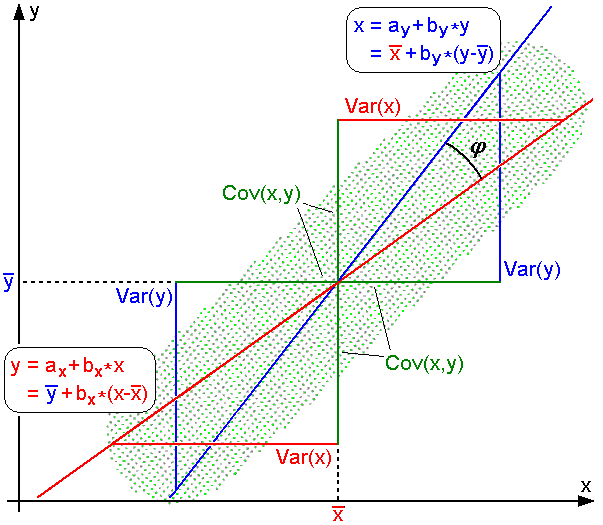
Pearson Correlation Coefficient
In statistics, the Pearson correlation coefficient (PCC) is a correlation coefficient that measures linear correlation between two sets of data. It is the ratio between the covariance of two variables and the product of their standard deviations; thus, it is essentially a normalized measurement of the covariance, such that the result always has a value between −1 and 1. As with covariance itself, the measure can only reflect a linear correlation of variables, and ignores many other types of relationships or correlations. As a simple example, one would expect the age and height of a sample of children from a school to have a Pearson correlation coefficient significantly greater than 0, but less than 1 (as 1 would represent an unrealistically perfect correlation). Naming and history It was developed by Karl Pearson from a related idea introduced by Francis Galton in the 1880s, and for which the mathematical formula was derived and published by Auguste Bravais in 1844. The nami ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Pearson Product-moment Correlation Coefficient
In statistics, the Pearson correlation coefficient (PCC) is a correlation coefficient that measures linear correlation between two sets of data. It is the ratio between the covariance of two variables and the product of their standard deviations; thus, it is essentially a normalized measurement of the covariance, such that the result always has a value between −1 and 1. As with covariance itself, the measure can only reflect a linear correlation of variables, and ignores many other types of relationships or correlations. As a simple example, one would expect the age and height of a sample of children from a school to have a Pearson correlation coefficient significantly greater than 0, but less than 1 (as 1 would represent an unrealistically perfect correlation). Naming and history It was developed by Karl Pearson from a related idea introduced by Francis Galton in the 1880s, and for which the mathematical formula was derived and published by Auguste Bravais in 1844. The naming ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Intra-class Correlation
In statistics, the intraclass correlation, or the intraclass correlation coefficient (ICC), is a descriptive statistic that can be used when quantitative measurements are made on units that are organized into groups. It describes how strongly units in the same group resemble each other. While it is viewed as a type of correlation, unlike most other correlation measures, it operates on data structured as groups rather than data structured as paired observations. The ''intraclass correlation'' is commonly used to quantify the degree to which individuals with a fixed degree of relatedness (e.g. full siblings) resemble each other in terms of a quantitative trait (see heritability). Another prominent application is the assessment of consistency or reproducibility of quantitative measurements made by different observers measuring the same quantity. Early ICC definition: unbiased but complex formula The earliest work on intraclass correlations focused on the case of paired measu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Statistics In Medicine (journal)
'' Statistics in Medicine'' is a peer-reviewed statistics journal published by Wiley. Established in 1982, the journal publishes articles on medical statistics. The journal is indexed by ''Mathematical Reviews'' and SCOPUS. According to the ''Journal Citation Reports'', the journal has a 2023 impact factor The impact factor (IF) or journal impact factor (JIF) of an academic journal is a type of journal ranking. Journals with higher impact factor values are considered more prestigious or important within their field. The Impact Factor of a journa ... of 1.8. References External links * Medical statistics journals Academic journals established in 1982 English-language journals Wiley (publisher) academic journals {{statistics-journal-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Jossey-Bass
John Wiley & Sons, Inc., commonly known as Wiley (), is an American multinational publishing company that focuses on academic publishing and instructional materials. The company was founded in 1807 and produces books, journals, and encyclopedias, in print and electronically, as well as online products and services, training materials, and educational materials for undergraduate, graduate, and continuing education students. History The company was established in 1807 when Charles Wiley opened a print shop in Manhattan. The company was the publisher of 19th century American literary figures like James Fenimore Cooper, Washington Irving, Herman Melville, and Edgar Allan Poe, as well as of legal, religious, and other non-fiction titles. The firm took its current name in 1865. Wiley later shifted its focus to scientific, technical, and engineering subject areas, abandoning its literary interests. Wiley's son John (born in Flatbush, New York, October 4, 1808; died in East Oran ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
San Francisco
San Francisco, officially the City and County of San Francisco, is a commercial, Financial District, San Francisco, financial, and Culture of San Francisco, cultural center of Northern California. With a population of 827,526 residents as of 2024, San Francisco is the List of California cities by population, fourth-most populous city in the U.S. state of California and the List of United States cities by population, 17th-most populous in the United States. San Francisco has a land area of at the upper end of the San Francisco Peninsula and is the County statistics of the United States, fifth-most densely populated U.S. county. Among U.S. cities proper with over 250,000 residents, San Francisco is ranked first by per capita income and sixth by aggregate income as of 2023. San Francisco anchors the Metropolitan statistical area#United States, 13th-most populous metropolitan statistical area in the U.S., with almost 4.6 million residents in 2023. The larger San Francisco Bay Area ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |