|
Comparison Of Vector Algebra And Geometric Algebra
Geometric algebra is an extension of vector algebra, providing additional algebraic structures on vector spaces, with geometric interpretations. Vector algebra uses all dimensions and signatures, as does geometric algebra, notably 3+1 spacetime as well as 2 dimensions. Basic concepts and operations Geometric algebra (GA) is an extension or completion of vector algebra (VA). The reader is herein assumed to be familiar with the basic concepts and operations of VA and this article will mainly concern itself with operations in \mathcal G_ the GA of 3D space (nor is this article intended to be mathematically rigorous). In GA, vectors are not normally written boldface as the meaning is usually clear from the context. The fundamental difference is that GA provides a new product of vectors called the "geometric product". Elements of GA are graded multivectors: scalars are grade 0, usual vectors are grade 1, bivectors are grade 2 and the highest grade (3 in the 3D case) is traditionally ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometric Algebra
In mathematics, a geometric algebra (also known as a Clifford algebra) is an algebra that can represent and manipulate geometrical objects such as vectors. Geometric algebra is built out of two fundamental operations, addition and the geometric product. Multiplication of vectors results in higher-dimensional objects called multivectors. Compared to other formalisms for manipulating geometric objects, geometric algebra is noteworthy for supporting vector division (though generally not by all elements) and addition of objects of different dimensions. The geometric product was first briefly mentioned by Hermann Grassmann, who was chiefly interested in developing the closely related exterior algebra. In 1878, William Kingdon Clifford greatly expanded on Grassmann's work to form what are now usually called Clifford algebras in his honor (although Clifford himself chose to call them "geometric algebras"). Clifford defined the Clifford algebra and its product as a unification of the Gras ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bivector
In mathematics, a bivector or 2-vector is a quantity in exterior algebra or geometric algebra that extends the idea of scalars and vectors. Considering a scalar as a degree-zero quantity and a vector as a degree-one quantity, a bivector is of degree two. Bivectors have applications in many areas of mathematics and physics. They are related to complex numbers in two dimensions and to both pseudovectors and vector quaternions in three dimensions. They can be used to generate rotations in a space of any number of dimensions, and are a useful tool for classifying such rotations. Geometrically, a simple bivector can be interpreted as characterizing a directed plane segment (or oriented plane segment), much as vectors can be thought of as characterizing '' directed line segments''. The bivector has an ''attitude'' (or direction) of the plane spanned by and , has an area that is a scalar multiple of any reference plane segment with the same attitude (and in geometric algebra, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gram Determinant
In linear algebra, the Gram matrix (or Gramian matrix, Gramian) of a set of vectors v_1,\dots, v_n in an inner product space is the Hermitian matrix of inner products, whose entries are given by the inner product G_ = \left\langle v_i, v_j \right\rangle., p.441, Theorem 7.2.10 If the vectors v_1,\dots, v_n are the columns of matrix X then the Gram matrix is X^\dagger X in the general case that the vector coordinates are complex numbers, which simplifies to X^\top X for the case that the vector coordinates are real numbers. An important application is to compute linear independence: a set of vectors are linearly independent if and only if the #Gram determinant, Gram determinant (the determinant of the Gram matrix) is non-zero. It is named after Jørgen Pedersen Gram. Examples For finite-dimensional real vectors in \mathbb^n with the usual Euclidean dot product, the Gram matrix is G = V^\top V, where V is a matrix whose columns are the vectors v_k and V^\top is its transpose whose r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dot Product
In mathematics, the dot product or scalar productThe term ''scalar product'' means literally "product with a Scalar (mathematics), scalar as a result". It is also used for other symmetric bilinear forms, for example in a pseudo-Euclidean space. Not to be confused with scalar multiplication. is an algebraic operation that takes two equal-length sequences of numbers (usually coordinate vectors), and returns a single number. In Euclidean geometry, the dot product of the Cartesian coordinates of two Euclidean vector, vectors is widely used. It is often called the inner product (or rarely the projection product) of Euclidean space, even though it is not the only inner product that can be defined on Euclidean space (see ''Inner product space'' for more). It should not be confused with the cross product. Algebraically, the dot product is the sum of the Product (mathematics), products of the corresponding entries of the two sequences of numbers. Geometrically, it is the product of the Euc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
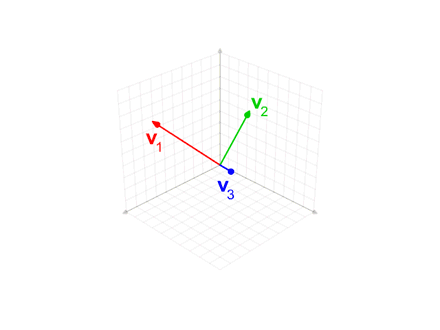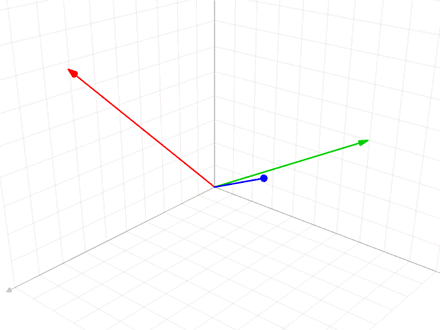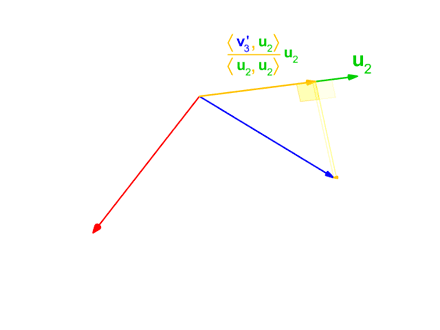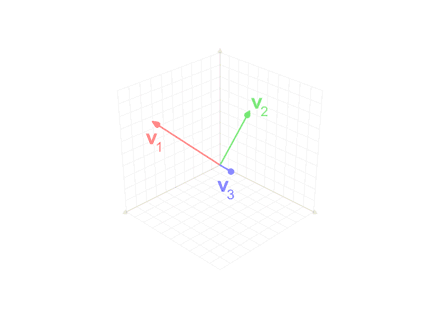
Gram–Schmidt Process
In mathematics, particularly linear algebra and numerical analysis, the Gram–Schmidt process or Gram-Schmidt algorithm is a way of finding a set of two or more vectors that are perpendicular to each other. By technical definition, it is a method of constructing an orthonormal basis from a set of vector (geometry), vectors in an inner product space, most commonly the Euclidean space \mathbb^n equipped with the standard inner product. The Gram–Schmidt process takes a finite set, finite, linearly independent set of vectors S = \ for and generates an orthogonal set S' = \ that spans the same k-dimensional subspace of \mathbb^n as S. The method is named after Jørgen Pedersen Gram and Erhard Schmidt, but Pierre-Simon Laplace had been familiar with it before Gram and Schmidt. In the theory of Lie group decompositions, it is generalized by the Iwasawa decomposition. The application of the Gram–Schmidt process to the column vectors of a full column rank (linear algebra), rank mat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parallelogram
In Euclidean geometry, a parallelogram is a simple polygon, simple (non-list of self-intersecting polygons, self-intersecting) quadrilateral with two pairs of Parallel (geometry), parallel sides. The opposite or facing sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of equal measure. The congruence (geometry), congruence of opposite sides and opposite angles is a direct consequence of the Euclidean parallel postulate and neither condition can be proven without appealing to the Euclidean parallel postulate or one of its equivalent formulations. By comparison, a quadrilateral with at least one pair of parallel sides is a trapezoid in American English or a trapezium in British English. The three-dimensional counterpart of a parallelogram is a parallelepiped. The word "parallelogram" comes from the Greek παραλληλό-γραμμον, ''parallēló-grammon'', which means "a shape of parallel lines". Special cases *Rectangle – A par ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cramer's Rule
In linear algebra, Cramer's rule is an explicit formula for the solution of a system of linear equations with as many equations as unknowns, valid whenever the system has a unique solution. It expresses the solution in terms of the determinants of the (square) coefficient matrix and of matrices obtained from it by replacing one column by the column vector of right-sides of the equations. It is named after Gabriel Cramer, who published the rule for an arbitrary number of unknowns in 1750, although Colin Maclaurin also published special cases of the rule in 1748, and possibly knew of it as early as 1729. Cramer's rule, implemented in a naive way, is computationally inefficient for systems of more than two or three equations. In the case of equations in unknowns, it requires computation of determinants, while Gaussian elimination produces the result with the same (up to a constant factor independent of ) computational complexity as the computation of a single determinant. Moreo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linearity
In mathematics, the term ''linear'' is used in two distinct senses for two different properties: * linearity of a '' function'' (or '' mapping''); * linearity of a '' polynomial''. An example of a linear function is the function defined by f(x)=(ax,bx) that maps the real line to a line in the Euclidean plane R2 that passes through the origin. An example of a linear polynomial in the variables X, Y and Z is aX+bY+cZ+d. Linearity of a mapping is closely related to '' proportionality''. Examples in physics include the linear relationship of voltage and current in an electrical conductor ( Ohm's law), and the relationship of mass and weight. By contrast, more complicated relationships, such as between velocity and kinetic energy, are '' nonlinear''. Generalized for functions in more than one dimension, linearity means the property of a function of being compatible with addition and scaling, also known as the superposition principle. Linearity of a polynomial means that it ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Distributivity
In mathematics, the distributive property of binary operations is a generalization of the distributive law, which asserts that the equality x \cdot (y + z) = x \cdot y + x \cdot z is always true in elementary algebra. For example, in elementary arithmetic, one has 2 \cdot (1 + 3) = (2 \cdot 1) + (2 \cdot 3). Therefore, one would say that multiplication ''distributes'' over addition. This basic property of numbers is part of the definition of most algebraic structures that have two operations called addition and multiplication, such as complex numbers, polynomials, matrices, rings, and fields. It is also encountered in Boolean algebra and mathematical logic, where each of the logical and (denoted \,\land\,) and the logical or (denoted \,\lor\,) distributes over the other. Definition Given a set S and two binary operators \,*\, and \,+\, on S, *the operation \,*\, is over (or with respect to) \,+\, if, given any elements x, y, \text z of S, x * (y + z) = (x * y) + (x * z) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Anti-commutative
In mathematics, anticommutativity is a specific property of some non-commutative mathematical operations. Swapping the position of two arguments of an antisymmetric operation yields a result which is the ''inverse'' of the result with unswapped arguments. The notion '' inverse'' refers to a group structure on the operation's codomain, possibly with another operation. Subtraction is an anticommutative operation because commuting the operands of gives for example, Another prominent example of an anticommutative operation is the Lie bracket. In mathematical physics, where symmetry is of central importance, or even just in multilinear algebra these operations are mostly (multilinear with respect to some vector structures and then) called antisymmetric operations, and when they are not already of arity greater than two, extended in an associative setting to cover more than two arguments. Definition If A, B are two abelian groups, a bilinear map f\colon A^2 \to B is anticommut ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vector Space
In mathematics and physics, a vector space (also called a linear space) is a set (mathematics), set whose elements, often called vector (mathematics and physics), ''vectors'', can be added together and multiplied ("scaled") by numbers called scalar (mathematics), ''scalars''. The operations of vector addition and scalar multiplication must satisfy certain requirements, called ''vector axioms''. Real vector spaces and complex vector spaces are kinds of vector spaces based on different kinds of scalars: real numbers and complex numbers. Scalars can also be, more generally, elements of any field (mathematics), field. Vector spaces generalize Euclidean vectors, which allow modeling of Physical quantity, physical quantities (such as forces and velocity) that have not only a Magnitude (mathematics), magnitude, but also a Orientation (geometry), direction. The concept of vector spaces is fundamental for linear algebra, together with the concept of matrix (mathematics), matrices, which ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Space Form
In mathematics, a space form is a complete Riemannian manifold ''M'' of constant sectional curvature ''K''. The three most fundamental examples are Euclidean ''n''-space, the ''n''-dimensional sphere, and hyperbolic space, although a space form need not be simply connected. Reduction to generalized crystallography The Killing–Hopf theorem of Riemannian geometry states that the universal cover of an ''n''-dimensional space form M^n with curvature K = -1 is isometric to H^n, hyperbolic space, with curvature K = 0 is isometric to R^n, Euclidean ''n''-space, and with curvature K = +1 is isometric to S^n, the n-dimensional sphere of points distance 1 from the origin in R^. By rescaling the Riemannian metric on H^n, we may create a space M_K of constant curvature K for any K 0. Thus the universal cover of a space form M with constant curvature K is isometric to M_K. This reduces the problem of studying space forms to studying discrete groups of isometries \Gamma of M_K which ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |