 |
Circular Error Probable
Circular error probable (CEP),Circular Error Probable (CEP), Air Force Operational Test and Evaluation Center Technical Paper 6, Ver 2, July 1987, p. 1 also circular error probability or circle of equal probability, is a measure of a weapon system's Accuracy and precision, precision in the military science of ballistics. It is defined as the radius of a circle, centered on the aimpoint, that is expected to enclose the landing points of 50% of the Round (firearms), rounds; said otherwise, it is the median error radius, which is a 50% confidence interval. That is, if a given munitions design has a CEP of 100 m, when 100 munitions are targeted at the same point, an average of 50 will fall within a circle with a radius of 100 m about that point. There are associated concepts, such as the DRMS (distance root mean square), which is the square root of the average squared distance error, a form of the standard deviation. Another is the R95, which is the radius of the circle ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
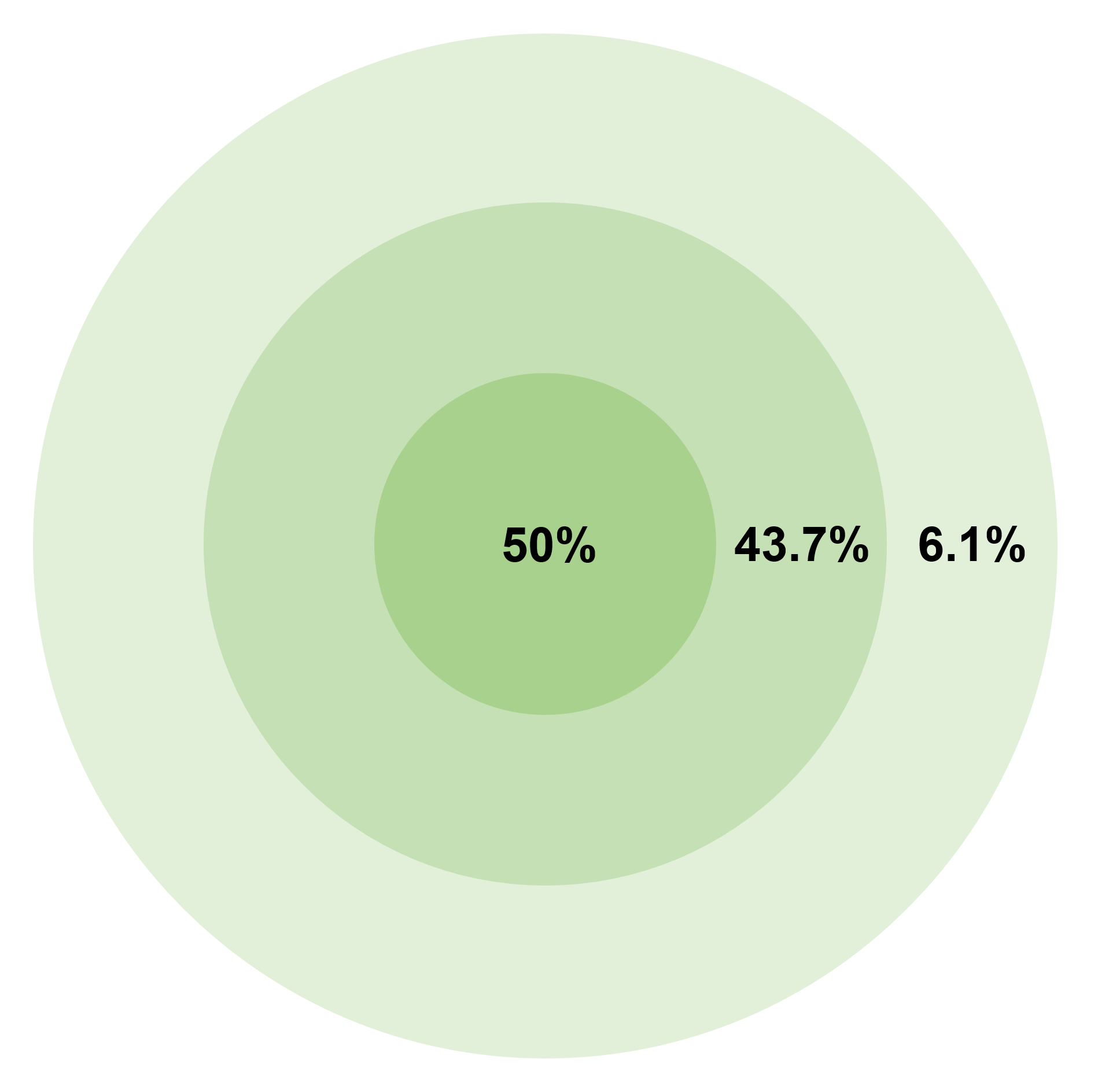
Circular Error Probable - Percentage
*
{{disambiguation ...
Circular may refer to: * The shape of a circle * ''Circular'' (album), a 2006 album by Spanish singer Vega * Circular letter (other), a document addressed to many destinations ** Government circular, a written statement of government policy **Circulaire * Circular reasoning, a type of logical fallacy * Circular reference *Circular Quay, Australia *Circular Park, Armenia See also * Circular DNA (other) * Circular Line (other) * Circularity (other) Circularity may refer to: *Circular definition *Circular economy *Circular reasoning Circular reasoning (, "circle in proving"; also known as circular logic) is a fallacy, logical fallacy in which the reasoner begins with what they are trying ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Mean
A mean is a quantity representing the "center" of a collection of numbers and is intermediate to the extreme values of the set of numbers. There are several kinds of means (or "measures of central tendency") in mathematics, especially in statistics. Each attempts to summarize or typify a given group of data, illustrating the magnitude and sign of the data set. Which of these measures is most illuminating depends on what is being measured, and on context and purpose. The ''arithmetic mean'', also known as "arithmetic average", is the sum of the values divided by the number of values. The arithmetic mean of a set of numbers ''x''1, ''x''2, ..., x''n'' is typically denoted using an overhead bar, \bar. If the numbers are from observing a sample of a larger group, the arithmetic mean is termed the '' sample mean'' (\bar) to distinguish it from the group mean (or expected value) of the underlying distribution, denoted \mu or \mu_x. Outside probability and statistics, a wide rang ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Root Mean Square
In mathematics, the root mean square (abbrev. RMS, or rms) of a set of values is the square root of the set's mean square. Given a set x_i, its RMS is denoted as either x_\mathrm or \mathrm_x. The RMS is also known as the quadratic mean (denoted M_2), a special case of the generalized mean. The RMS of a continuous function is denoted f_\mathrm and can be defined in terms of an integral of the square of the function. In estimation theory, the root-mean-square deviation of an estimator measures how far the estimator strays from the data. Definition The RMS value of a set of values (or a continuous-time waveform) is the square root of the arithmetic mean of the squares of the values, or the square of the function that defines the continuous waveform. In the case of a set of ''n'' values \, the RMS is : x_\text = \sqrt. The corresponding formula for a continuous function (or waveform) ''f''(''t'') defined over the interval T_1 \le t \le T_2 is : f_\text = \sqrt , and the R ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Rayleigh Distribution
In probability theory and statistics, the Rayleigh distribution is a continuous probability distribution for nonnegative-valued random variables. Up to rescaling, it coincides with the chi distribution with two degrees of freedom. The distribution is named after Lord Rayleigh (). A Rayleigh distribution is often observed when the overall magnitude of a vector in the plane is related to its directional components. One example where the Rayleigh distribution naturally arises is when wind velocity is analyzed in two dimensions. Assuming that each component is uncorrelated, normally distributed with equal variance, and zero mean, which is infrequent, then the overall wind speed (vector magnitude) will be characterized by a Rayleigh distribution. A second example of the distribution arises in the case of random complex numbers whose real and imaginary components are independently and identically distributed Gaussian with equal variance and zero mean. In that case, the absolute v ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Uncorrelated
In probability theory and statistics, two real-valued random variables, X, Y, are said to be uncorrelated if their covariance, \operatorname ,Y= \operatorname Y- \operatorname \operatorname /math>, is zero. If two variables are uncorrelated, there is no linear relationship between them. Uncorrelated random variables have a Pearson correlation coefficient, when it exists, of zero, except in the trivial case when either variable has zero variance (is a constant). In this case the correlation is undefined. In general, uncorrelatedness is not the same as orthogonality, except in the special case where at least one of the two random variables has an expected value of 0. In this case, the covariance is the expectation of the product, and X and Y are uncorrelated if and only if In logic and related fields such as mathematics and philosophy, "if and only if" (often shortened as "iff") is paraphrased by the biconditional, a logical connective between statements. The bicondit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Random Variable
A random variable (also called random quantity, aleatory variable, or stochastic variable) is a Mathematics, mathematical formalization of a quantity or object which depends on randomness, random events. The term 'random variable' in its mathematical definition refers to neither randomness nor variability but instead is a mathematical function (mathematics), function in which * the Domain of a function, domain is the set of possible Outcome (probability), outcomes in a sample space (e.g. the set \ which are the possible upper sides of a flipped coin heads H or tails T as the result from tossing a coin); and * the Range of a function, range is a measurable space (e.g. corresponding to the domain above, the range might be the set \ if say heads H mapped to -1 and T mapped to 1). Typically, the range of a random variable is a subset of the Real number, real numbers. Informally, randomness typically represents some fundamental element of chance, such as in the roll of a dice, d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Percentile
In statistics, a ''k''-th percentile, also known as percentile score or centile, is a score (e.g., a data point) a given percentage ''k'' of all scores in its frequency distribution exists ("exclusive" definition) or a score a given percentage of the all scores exists ("inclusive" definition); i.e. a score in the ''k''-th percentile would be above approximately ''k''% of all scores in its set. For example, the 97th percentile of data is a data point below which 97% of all data points exist (by the exclusive definition). Percentiles depends on how scores are arranged. Percentiles are a type of quantiles, obtained adopting a subdivision into 100 groups. The 25th percentile is also known as the first '' quartile'' (''Q''1), the 50th percentile as the ''median'' or second quartile (''Q''2), and the 75th percentile as the third quartile (''Q''3). For example, the 50th percentile (median) is the score (or , depending on the definition) which 50% of the scores in the distribution are ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Circle
A circle is a shape consisting of all point (geometry), points in a plane (mathematics), plane that are at a given distance from a given point, the Centre (geometry), centre. The distance between any point of the circle and the centre is called the radius. The length of a line segment connecting two points on the circle and passing through the centre is called the diameter. A circle bounds a region of the plane called a Disk (mathematics), disc. The circle has been known since before the beginning of recorded history. Natural circles are common, such as the full moon or a slice of round fruit. The circle is the basis for the wheel, which, with related inventions such as gears, makes much of modern machinery possible. In mathematics, the study of the circle has helped inspire the development of geometry, astronomy and calculus. Terminology * Annulus (mathematics), Annulus: a ring-shaped object, the region bounded by two concentric circles. * Circular arc, Arc: any Connected ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Radius
In classical geometry, a radius (: radii or radiuses) of a circle or sphere is any of the line segments from its Centre (geometry), center to its perimeter, and in more modern usage, it is also their length. The radius of a regular polygon is the line segment or distance from its center to any of its Vertex (geometry), vertices. The name comes from the Latin ''radius'', meaning ray but also the spoke of a chariot wheel.Definition of Radius at dictionary.reference.com. Accessed on 2009-08-08. The typical abbreviation and mathematical symbol for radius is ''R'' or ''r''. By extension, the diameter ''D'' is defined as twice the radius:Definition of radius at mathwords.com. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Covariance
In probability theory and statistics, covariance is a measure of the joint variability of two random variables. The sign of the covariance, therefore, shows the tendency in the linear relationship between the variables. If greater values of one variable mainly correspond with greater values of the other variable, and the same holds for lesser values (that is, the variables tend to show similar behavior), the covariance is positive. In the opposite case, when greater values of one variable mainly correspond to lesser values of the other (that is, the variables tend to show opposite behavior), the covariance is negative. The magnitude of the covariance is the geometric mean of the variances that are in common for the two random variables. The Pearson product-moment correlation coefficient, correlation coefficient normalizes the covariance by dividing by the geometric mean of the total variances for the two random variables. A distinction must be made between (1) the covariance of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Variance
In probability theory and statistics, variance is the expected value of the squared deviation from the mean of a random variable. The standard deviation (SD) is obtained as the square root of the variance. Variance is a measure of dispersion, meaning it is a measure of how far a set of numbers is spread out from their average value. It is the second central moment of a distribution, and the covariance of the random variable with itself, and it is often represented by \sigma^2, s^2, \operatorname(X), V(X), or \mathbb(X). An advantage of variance as a measure of dispersion is that it is more amenable to algebraic manipulation than other measures of dispersion such as the expected absolute deviation; for example, the variance of a sum of uncorrelated random variables is equal to the sum of their variances. A disadvantage of the variance for practical applications is that, unlike the standard deviation, its units differ from the random variable, which is why the standard devi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |