|
Cauchy Formula For Repeated Integration
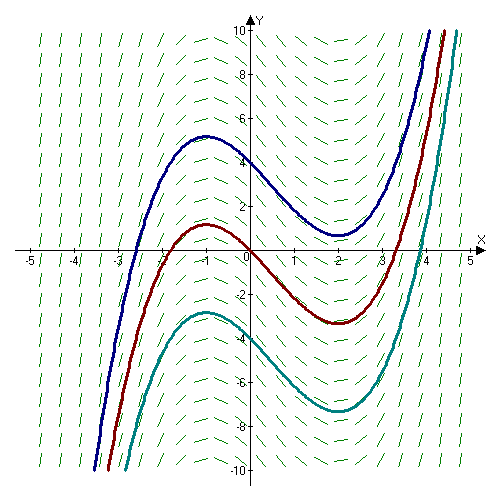
The Cauchy formula for repeated integration, named after Augustin-Louis Cauchy, allows one to compress ''n'' antiderivatives of a function into a single integral (cf. Cauchy's formula). For non-integer ''n'' it yields the definition of fractional integrals and (with ''n'' 0, and the factorial is replaced by the gamma function. The two formulas agree when \alpha \in \Z_. Both the Cauchy formula and the Riemann–Liouville integral are generalized to arbitrary dimensions by the Riesz potential. In fractional calculus, these formulae can be used to construct a differintegral, allowing one to differentiate or integrate a fractional number of times. Differentiating a fractional number of times can be accomplished by fractional integration, then differentiating the result. References * Augustin-Louis Cauchy Baron Augustin-Louis Cauchy ( , , ; ; 21 August 1789 – 23 May 1857) was a French mathematician, engineer, and physicist. He was one of the first to rigorous ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Augustin-Louis Cauchy
Baron Augustin-Louis Cauchy ( , , ; ; 21 August 1789 – 23 May 1857) was a French mathematician, engineer, and physicist. He was one of the first to rigorously state and prove the key theorems of calculus (thereby creating real analysis), pioneered the field complex analysis, and the study of permutation groups in abstract algebra. Cauchy also contributed to a number of topics in mathematical physics, notably continuum mechanics. A profound mathematician, Cauchy had a great influence over his contemporaries and successors; Hans Freudenthal stated: : "More concepts and theorems have been named for Cauchy than for any other mathematician (in elasticity alone there are sixteen concepts and theorems named for Cauchy)." Cauchy was a prolific worker; he wrote approximately eight hundred research articles and five complete textbooks on a variety of topics in the fields of mathematics and mathematical physics. Biography Youth and education Cauchy was the son of Lou ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Antidifferentiation
In calculus, an antiderivative, inverse derivative, primitive function, primitive integral or indefinite integral of a continuous function is a differentiable function whose derivative is equal to the original function . This can be stated symbolically as . The process of solving for antiderivatives is called antidifferentiation (or indefinite integration), and its opposite operation is called ''differentiation'', which is the process of finding a derivative. Antiderivatives are often denoted by capital Roman letters such as and . Antiderivatives are related to definite integrals through the second fundamental theorem of calculus: the definite integral of a function over a closed interval where the function is Riemann integrable is equal to the difference between the values of an antiderivative evaluated at the endpoints of the interval. In physics, antiderivatives arise in the context of rectilinear motion (e.g., in explaining the relationship between position, velocity a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Antiderivative
In calculus, an antiderivative, inverse derivative, primitive function, primitive integral or indefinite integral of a continuous function is a differentiable function whose derivative is equal to the original function . This can be stated symbolically as . The process of solving for antiderivatives is called antidifferentiation (or indefinite integration), and its opposite operation is called ''differentiation'', which is the process of finding a derivative. Antiderivatives are often denoted by capital Roman letters such as and . Antiderivatives are related to definite integrals through the second fundamental theorem of calculus: the definite integral of a function over a closed interval where the function is Riemann integrable is equal to the difference between the values of an antiderivative evaluated at the endpoints of the interval. In physics, antiderivatives arise in the context of rectilinear motion (e.g., in explaining the relationship between position, veloc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fractional Integral
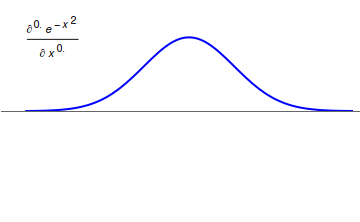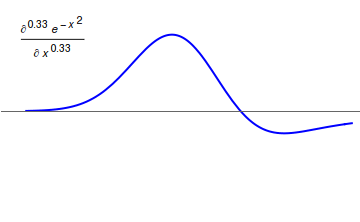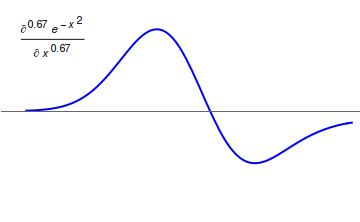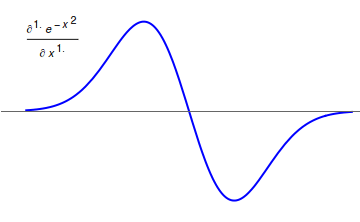
Fractional calculus is a branch of mathematical analysis that studies the several different possibilities of defining real number powers or complex number powers of the derivative, differentiation operator (mathematics), operator D D f(x) = \frac f(x)\,, and of the integral, integration operator J The symbol J is commonly used instead of the intuitive I in order to avoid confusion with other concepts identified by similar glyphs, such as identity (mathematics), identities. J f(x) = \int_0^x f(s) \,ds\,, and developing a calculus for such operators generalizing the classical one. In this context, the term ''powers'' refers to iterative application of a linear operator D to a function (mathematics), function that is, repeatedly function composition, composing D with itself, as in \begin D^n(f) &= (\underbrace_n)(f) \\ &= \underbrace_n (f)\cdots))). \end For example, one may ask for a meaningful interpretation of \sqrt = D^ as an analogue of the functional square root f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fractional Derivative
Fractional calculus is a branch of mathematical analysis that studies the several different possibilities of defining real number powers or complex number powers of the differentiation operator D D f(x) = \frac f(x)\,, and of the integration operator J The symbol J is commonly used instead of the intuitive I in order to avoid confusion with other concepts identified by similar glyphs, such as identities. J f(x) = \int_0^x f(s) \,ds\,, and developing a calculus for such operators generalizing the classical one. In this context, the term ''powers'' refers to iterative application of a linear operator D to a function that is, repeatedly composing D with itself, as in \begin D^n(f) &= (\underbrace_n)(f) \\ &= \underbrace_n (f)\cdots))). \end For example, one may ask for a meaningful interpretation of \sqrt = D^ as an analogue of the functional square root for the differentiation operator, that is, an expression for some linear operator that, when applied to any f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Continuous Function
In mathematics, a continuous function is a function such that a small variation of the argument induces a small variation of the value of the function. This implies there are no abrupt changes in value, known as '' discontinuities''. More precisely, a function is continuous if arbitrarily small changes in its value can be assured by restricting to sufficiently small changes of its argument. A discontinuous function is a function that is . Until the 19th century, mathematicians largely relied on intuitive notions of continuity and considered only continuous functions. The epsilon–delta definition of a limit was introduced to formalize the definition of continuity. Continuity is one of the core concepts of calculus and mathematical analysis, where arguments and values of functions are real and complex numbers. The concept has been generalized to functions between metric spaces and between topological spaces. The latter are the most general continuous functions, and their d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Repeated Integral
In multivariable calculus, an iterated integral is the result of applying integrals to a function of more than one variable (for example f(x,y) or f(x,y,z)) in such a way that each of the integrals considers some of the variables as given constants. For example, the function f(x,y), if y is considered a given parameter, can be integrated with respect to x, \int f(x,y)\,dx. The result is a function of y and therefore its integral can be considered. If this is done, the result is the iterated integral :\int\left(\int f(x,y)\,dx\right)\,dy. It is key for the notion of iterated integrals that this is different, in principle, from the multiple integral :\iint f(x,y)\,dx\,dy. In general, although these two can be different, Fubini's theorem In mathematical analysis, Fubini's theorem characterizes the conditions under which it is possible to compute a double integral by using an iterated integral. It was introduced by Guido Fubini in 1907. The theorem states that if a function is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Induction
Mathematical induction is a method for mathematical proof, proving that a statement P(n) is true for every natural number n, that is, that the infinitely many cases P(0), P(1), P(2), P(3), \dots all hold. This is done by first proving a simple case, then also showing that if we assume the claim is true for a given case, then the next case is also true. Informal metaphors help to explain this technique, such as falling dominoes or climbing a ladder: A proof by induction consists of two cases. The first, the base case, proves the statement for n = 0 without assuming any knowledge of other cases. The second case, the induction step, proves that ''if'' the statement holds for any given case n = k, ''then'' it must also hold for the next case n = k + 1. These two steps establish that the statement holds for every natural number n. The base case does not necessarily begin with n = 0, but often with n = 1, and possibly with any fixed natural number n = N, establishing the trut ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Leibniz Integral Rule
In calculus, the Leibniz integral rule for differentiation under the integral sign, named after Gottfried Wilhelm Leibniz, states that for an integral of the form \int_^ f(x,t)\,dt, where -\infty < a(x), b(x) < \infty and the integrands are functions dependent on the derivative of this integral is expressible as where the partial derivative indicates that inside the integral, only the variation of with is considered in taking the derivative. In the special case where the functions and |
Riemann–Liouville Integral
In mathematics, the Riemann–Liouville integral associates with a real function f: \mathbb \rightarrow \mathbb another function of the same kind for each value of the parameter . The integral is a manner of generalization of the repeated antiderivative of in the sense that for positive integer values of , is an iterated antiderivative of of order . The Riemann–Liouville integral is named for Bernhard Riemann and Joseph Liouville, the latter of whom was the first to consider the possibility of fractional calculus in 1832. The operator agrees with the Euler transform, after Leonhard Euler, when applied to analytic functions. It was generalized to arbitrary dimensions by Marcel Riesz, who introduced the Riesz potential. Motivation The Riemann-Liouville integral is motivated from Cauchy formula for repeated integration. For a function continuous on the interval the Cauchy formula for -fold repeated integration states that I^n f(x) = f^(x) = \frac \int_a^x\left(x-t\ri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Factorial
In mathematics, the factorial of a non-negative denoted is the Product (mathematics), product of all positive integers less than or equal The factorial also equals the product of n with the next smaller factorial: \begin n! &= n \times (n-1) \times (n-2) \times (n-3) \times \cdots \times 3 \times 2 \times 1 \\ &= n\times(n-1)!\\ \end For example, 5! = 5\times 4! = 5 \times 4 \times 3 \times 2 \times 1 = 120. The value of 0! is 1, according to the convention for an empty product. Factorials have been discovered in several ancient cultures, notably in Indian mathematics in the canonical works of Jain literature, and by Jewish mystics in the Talmudic book ''Sefer Yetzirah''. The factorial operation is encountered in many areas of mathematics, notably in combinatorics, where its most basic use counts the possible distinct sequences – the permutations – of n distinct objects: there In mathematical analysis, factorials are used in power series for the ex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gamma Function
In mathematics, the gamma function (represented by Γ, capital Greek alphabet, Greek letter gamma) is the most common extension of the factorial function to complex numbers. Derived by Daniel Bernoulli, the gamma function \Gamma(z) is defined for all complex numbers z except non-positive integers, and for every positive integer z=n, \Gamma(n) = (n-1)!\,.The gamma function can be defined via a convergent improper integral for complex numbers with positive real part: \Gamma(z) = \int_0^\infty t^ e^\textt, \ \qquad \Re(z) > 0\,.The gamma function then is defined in the complex plane as the analytic continuation of this integral function: it is a meromorphic function which is holomorphic function, holomorphic except at zero and the negative integers, where it has simple Zeros and poles, poles. The gamma function has no zeros, so the reciprocal gamma function is an entire function. In fact, the gamma function corresponds to the Mellin transform of the negative exponential functi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |