|
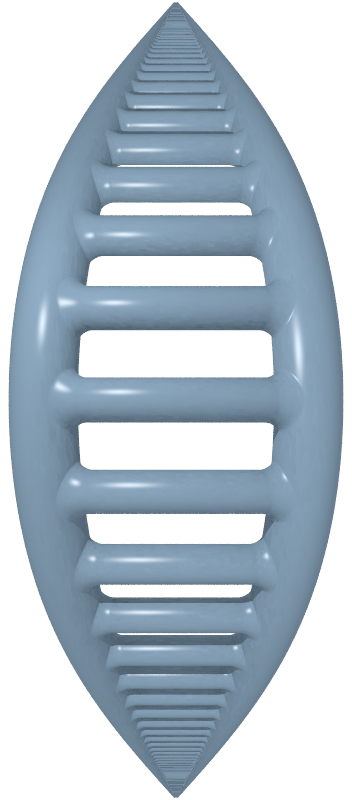
Cantor Tree Surface
In dynamical systems, the Cantor tree is an infinite-genus surface homeomorphic to a sphere with a Cantor set removed. The blooming Cantor tree is a Cantor tree with an infinite number of handles added in such a way that every end is a limit of handles. See also *Jacob's ladder surface * Loch Ness monster surface References {{reflist, refs= {{Citation , last1=Ghys , first1=Étienne , title=Topologie des feuilles génériques , doi=10.2307/2118526 , mr=1324140 , year=1995 , journal=Annals of Mathematics The ''Annals of Mathematics'' is a mathematical journal published every two months by Princeton University and the Institute for Advanced Study. History The journal was established as ''The Analyst'' in 1874 and with Joel E. Hendricks as t ... , series=Second Series , issn=0003-486X , volume=141 , issue=2 , pages=387–422, jstor=2118526 , language=fr {{Citation , last1=Walczak , first1=Paweł , title=Dynamics of foliations, groups and pseudogroups , ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Alexander Horned Sphere
The Alexander horned sphere is a pathological object in topology discovered by . It is a particular topological embedding of a two-dimensional sphere in three-dimensional space. Together with its inside, it is a topological 3-ball, the Alexander horned ball, and so is simply connected; i.e., every loop can be shrunk to a point while staying inside. However, the exterior is ''not'' simply connected, unlike the exterior of the usual round sphere. Construction The Alexander horned sphere is the particular (topological) embedding of a sphere in 3-dimensional Euclidean space obtained by the following construction, starting with a standard torus:. #Remove a radial slice of the torus. #Connect a standard punctured torus to each side of the cut, interlinked with the torus on the other side. #Repeat steps 1–2 on the two tori just added ''ad infinitum''. By considering only the points of the tori that are not removed at some stage, an embedding of the sphere with a Cantor set remov ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dynamical System
In mathematics, a dynamical system is a system in which a Function (mathematics), function describes the time dependence of a Point (geometry), point in an ambient space, such as in a parametric curve. Examples include the mathematical models that describe the swinging of a clock pendulum, fluid dynamics, the flow of water in a pipe, the Brownian motion, random motion of particles in the air, and population dynamics, the number of fish each springtime in a lake. The most general definition unifies several concepts in mathematics such as ordinary differential equations and ergodic theory by allowing different choices of the space and how time is measured. Time can be measured by integers, by real number, real or complex numbers or can be a more general algebraic object, losing the memory of its physical origin, and the space may be a manifold or simply a Set (mathematics), set, without the need of a Differentiability, smooth space-time structure defined on it. At any given time, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Genus (mathematics)
In mathematics, genus (: genera) has a few different, but closely related, meanings. Intuitively, the genus is the number of "holes" of a surface. A sphere has genus 0, while a torus has genus 1. Topology Orientable surfaces The genus of a connected, orientable surface is an integer representing the maximum number of cuttings along non-intersecting closed simple curves without rendering the resultant manifold disconnected. It is equal to the number of handles on it. Alternatively, it can be defined in terms of the Euler characteristic \chi, via the relationship \chi=2-2g for closed surfaces, where g is the genus. For surfaces with b boundary components, the equation reads \chi=2-2g-b. In layman's terms, the genus is the number of "holes" an object has ("holes" interpreted in the sense of doughnut holes; a hollow sphere would be considered as having zero holes in this sense). A torus has 1 such hole, while a sphere has 0. The green surface pictured above has 2 holes of the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Homeomorphism
In mathematics and more specifically in topology, a homeomorphism ( from Greek roots meaning "similar shape", named by Henri Poincaré), also called topological isomorphism, or bicontinuous function, is a bijective and continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are the mappings that preserve all the topological properties of a given space. Two spaces with a homeomorphism between them are called homeomorphic, and from a topological viewpoint they are the same. Very roughly speaking, a topological space is a geometric object, and a homeomorphism results from a continuous deformation of the object into a new shape. Thus, a square and a circle are homeomorphic to each other, but a sphere and a torus are not. However, this description can be misleading. Some continuous deformations do not produce homeomorphisms, such as the deformation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sphere
A sphere (from Ancient Greek, Greek , ) is a surface (mathematics), surface analogous to the circle, a curve. In solid geometry, a sphere is the Locus (mathematics), set of points that are all at the same distance from a given point in three-dimensional space.. That given point is the center (geometry), ''center'' of the sphere, and the distance is the sphere's ''radius''. The earliest known mentions of spheres appear in the work of the Greek mathematics, ancient Greek mathematicians. The sphere is a fundamental surface in many fields of mathematics. Spheres and nearly-spherical shapes also appear in nature and industry. Bubble (physics), Bubbles such as soap bubbles take a spherical shape in equilibrium. The Earth is spherical Earth, often approximated as a sphere in geography, and the celestial sphere is an important concept in astronomy. Manufactured items including pressure vessels and most curved mirrors and lenses are based on spheres. Spheres rolling, roll smoothly in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cantor Set
In mathematics, the Cantor set is a set of points lying on a single line segment that has a number of unintuitive properties. It was discovered in 1874 by Henry John Stephen Smith and mentioned by German mathematician Georg Cantor in 1883. Through consideration of this set, Cantor and others helped lay the foundations of modern point-set topology. The most common construction is the Cantor ternary set, built by removing the middle third of a line segment and then repeating the process with the remaining shorter segments. Cantor mentioned this ternary construction only in passing, as an example of a perfect set that is nowhere dense. More generally, in topology, a Cantor space is a topological space homeomorphic to the Cantor ternary set (equipped with its subspace topology). The Cantor set is naturally homeomorphic to the countable product ^ of the discrete two-point space \underline 2 . By a theorem of L. E. J. Brouwer, this is equivalent to being perfect, nonempty, compac ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
End (topology)
In topology, a branch of mathematics, the ends of a topological space are, roughly speaking, the connected components of the "ideal boundary" of the space. That is, each end represents a topologically distinct way to move to infinity within the space. Adding a point at each end yields a compactification of the original space, known as the end compactification. The notion of an end of a topological space was introduced by . Definition Let X be a topological space, and suppose that is an ascending sequence of compact subsets of X whose interiors cover X. Then X has one end for every sequence where each U_n is a connected component of X\setminus K_n. The number of ends does not depend on the specific sequence (K_i) of compact sets; there is a natural bijection between the sets of ends associated with any two such sequences. Using this definition, a neighborhood of an end (U_i) is an open set V such that V\supset U_n for some n. Such neighborhoods represent the neighborhood ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jacob's Ladder Surface
In mathematics, Jacob's ladder is a two-dimensional manifold, surface with infinite Genus (mathematics), genus and two End (topology), ends. It was named after Jacob's ladder by Étienne , because the surface can be constructed as the boundary of a ladder that is infinitely long in both directions. See also *Cantor tree surface *Loch Ness monster surface References * * Surfaces {{Topology-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Loch Ness Monster Surface
In mathematics, the Loch Ness monster is a surface with infinite genus but only one end. It appeared named this way already in a 1981 article by . The surface can be constructed by starting with a plane (which can be thought of as the surface of Loch Ness) and adding an infinite number of handles (which can be thought of as loops of the Loch Ness monster). See also * Cantor tree surface * Jacob's ladder surface In mathematics, Jacob's ladder is a two-dimensional manifold, surface with infinite Genus (mathematics), genus and two End (topology), ends. It was named after Jacob's ladder by Étienne , because the surface can be constructed as the boundary ... References * * * *{{Citation , last1=Arredondo , first1=John A. , last2=Ramírez-Maluendas , first2= Camilo, title=On the Infinite Loch Ness monster , url=http://cmuc.karlin.mff.cuni.cz/cmuc1704/abs/arredo.htm , doi=10.14712/1213-7243.2015.227 , year=2017 , journal= Commentationes Mathematicae Universitatis Ca ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Annals Of Mathematics
The ''Annals of Mathematics'' is a mathematical journal published every two months by Princeton University and the Institute for Advanced Study. History The journal was established as ''The Analyst'' in 1874 and with Joel E. Hendricks as the founding editor-in-chief. It was "intended to afford a medium for the presentation and analysis of any and all questions of interest or importance in pure and applied Mathematics, embracing especially all new and interesting discoveries in theoretical and practical astronomy, mechanical philosophy, and engineering". It was published in Des Moines, Iowa, and was the earliest American mathematics journal to be published continuously for more than a year or two. This incarnation of the journal ceased publication after its tenth year, in 1883, giving as an explanation Hendricks' declining health, but Hendricks made arrangements to have it taken over by new management, and it was continued from March 1884 as the ''Annals of Mathematics''. T ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fractals
In mathematics, a fractal is a Shape, geometric shape containing detailed structure at arbitrarily small scales, usually having a fractal dimension strictly exceeding the topological dimension. Many fractals appear similar at various scales, as illustrated in successive magnifications of the Mandelbrot set. This exhibition of similar patterns at increasingly smaller scales is called self-similarity, also known as expanding symmetry or unfolding symmetry; if this replication is exactly the same at every scale, as in the Menger sponge, the shape is called affine geometry, affine self-similar. Fractal geometry lies within the mathematical branch of measure theory. One way that fractals are different from finite geometric figures is how they Scaling (geometry), scale. Doubling the edge lengths of a filled polygon multiplies its area by four, which is two (the ratio of the new to the old side length) raised to the power of two (the conventional dimension of the filled polygon). ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |