|
Boolean Conjunctive Query
In the theory of relational databases, a Boolean conjunctive query is a conjunctive query without distinguished predicates, i.e., a query in the form R_1(t_1) \wedge \cdots \wedge R_n(t_n), where each R_i is a relation symbol and each t_i is a tuple of variables and constants; the number of elements in t_i is equal to the arity of R_i. Such a query evaluates to either true or false depending on whether the relations in the database contain the appropriate tuples of values, i.e. the conjunction is valid according to the facts in the database. As an example, if a database schema contains the relation symbols (binary, who's the father of whom) and (unary, who is employed), a conjunctive query could be Father(\text, x) \wedge Employed(x). This query evaluates to true if there exists an individual who is a child of Mark and employed. In other words, this query expresses the question: "does Mark have an employed child?" Complexity See also *Logical conjunction *Conjunctive quer ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
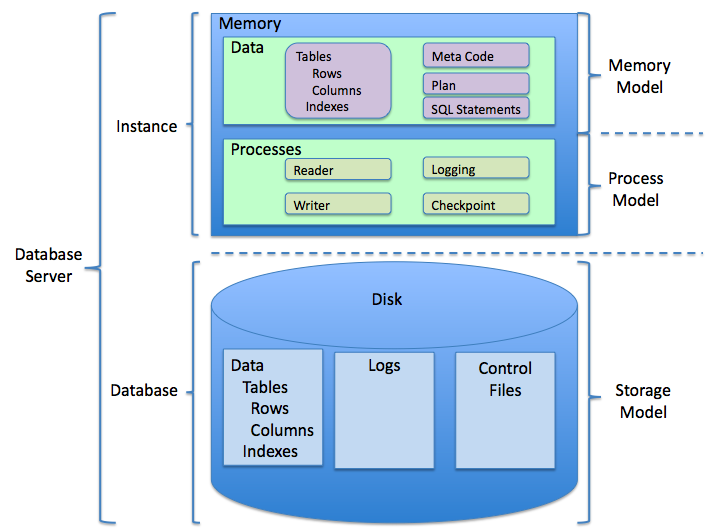 |
Relational Databases
A relational database (RDB) is a database based on the relational model of data, as proposed by E. F. Codd in 1970. A Relational Database Management System (RDBMS) is a type of database management system that stores data in a structured format using rows and columns. Many relational database systems are equipped with the option of using SQL (Structured Query Language) for querying and updating the database. History The concept of relational database was defined by E. F. Codd at IBM in 1970. Codd introduced the term ''relational'' in his research paper "A Relational Model of Data for Large Shared Data Banks". In this paper and later papers, he defined what he meant by ''relation''. One well-known definition of what constitutes a relational database system is composed of Codd's 12 rules. However, no commercial implementations of the relational model conform to all of Codd's rules, so the term has gradually come to describe a broader class of database systems, which at a m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Conjunctive Query
In database theory, a conjunctive query is a restricted form of first-order queries using the logical conjunction operator. Many first-order queries can be written as conjunctive queries. In particular, a large part of queries issued on relational databases can be expressed in this way. Conjunctive queries also have a number of desirable theoretical properties that larger classes of queries (e.g., the relational algebra queries) do not share. Definition The conjunctive queries are the fragment of (domain independent) first-order logic given by the set of formulae that can be constructed from atomic formulae using conjunction ∧ and existential quantification ∃, but not using disjunction ∨, negation ¬, or universal quantification ∀. Each such formula can be rewritten (efficiently) into an equivalent formula in prenex normal form, thus this form is usually simply assumed. Thus conjunctive queries are of the following general form: :(x_1, \ldots, x_k).\exists x_, \ldo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Tuple
In mathematics, a tuple is a finite sequence or ''ordered list'' of numbers or, more generally, mathematical objects, which are called the ''elements'' of the tuple. An -tuple is a tuple of elements, where is a non-negative integer. There is only one 0-tuple, called the ''empty tuple''. A 1-tuple and a 2-tuple are commonly called a singleton and an ordered pair, respectively. The term ''"infinite tuple"'' is occasionally used for ''"infinite sequences"''. Tuples are usually written by listing the elements within parentheses "" and separated by commas; for example, denotes a 5-tuple. Other types of brackets are sometimes used, although they may have a different meaning. An -tuple can be formally defined as the image of a function that has the set of the first natural numbers as its domain. Tuples may be also defined from ordered pairs by a recurrence starting from an ordered pair; indeed, an -tuple can be identified with the ordered pair of its first elements and its t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Arity
In logic, mathematics, and computer science, arity () is the number of arguments or operands taken by a function, operation or relation. In mathematics, arity may also be called rank, but this word can have many other meanings. In logic and philosophy, arity may also be called adicity and degree. In linguistics, it is usually named valency. Examples In general, functions or operators with a given arity follow the naming conventions of ''n''-based numeral systems, such as binary and hexadecimal. A Latin prefix is combined with the -ary suffix. For example: * A nullary function takes no arguments. ** Example: f()=2 * A unary function takes one argument. ** Example: f(x)=2x * A binary function takes two arguments. ** Example: f(x,y)=2xy * A ternary function takes three arguments. ** Example: f(x,y,z)=2xyz * An ''n''-ary function takes ''n'' arguments. ** Example: f(x_1, x_2, \ldots, x_n)=2\prod_^n x_i Nullary A constant can be treated as the output of an operation o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Validity (logic)
In logic, specifically in deductive reasoning, an argument is valid if and only if it takes a form that makes it impossible for the premises to be truth, true and the conclusion nevertheless to be False (logic), false. It is not required for a valid argument to have premises that are actually true, but to have premises that, if they were true, would guarantee the truth of the argument's conclusion. Valid arguments must be clearly expressed by means of sentences called well-formed formula, well-formed formulas (also called ''wffs'' or simply ''formulas''). The validity of an argument can be tested, proved or disproved, and depends on its logical form. Arguments In logic, an argument is a set of related statements expressing the ''premises'' (which may consists of non-empirical evidence, empirical evidence or may contain some axiomatic truths) and a ''necessary conclusion based on the relationship of the premises.'' An argument is ''valid'' if and only if it would be contradicto ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Database Schema
The database schema is the structure of a database described in a formal language supported typically by a relational database management system (RDBMS). The term "wikt:schema, schema" refers to the organization of data as a blueprint of how the database is constructed (divided into database tables in the case of relational databases). The formal definition of a database schema is a set of formulas (sentences) called integrity constraints imposed on a database. These integrity constraints ensure compatibility between parts of the schema. All constraints are expressible in the same language. A database can be considered a structure in realization of the database language. The states of a created conceptual schema are transformed into an explicit mapping, the database schema. This describes how real-world entities are Data modeling, modeled in the database. "A database schema specifies, based on the database administrator's knowledge of possible applications, the facts that can ent ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Logical Conjunction
In logic, mathematics and linguistics, ''and'' (\wedge) is the Truth function, truth-functional operator of conjunction or logical conjunction. The logical connective of this operator is typically represented as \wedge or \& or K (prefix) or \times or \cdot in which \wedge is the most modern and widely used. The ''and'' of a set of operands is true if and only if ''all'' of its operands are true, i.e., A \land B is true if and only if A is true and B is true. An operand of a conjunction is a conjunct. Beyond logic, the term "conjunction" also refers to similar concepts in other fields: * In natural language, the denotation of expressions such as English language, English "Conjunction (grammar), and"; * In programming languages, the Short-circuit evaluation, short-circuit and Control flow, control structure; * In set theory, Intersection (set theory), intersection. * In Lattice (order), lattice theory, logical conjunction (Infimum and supremum, greatest lower bound). Notati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Conjunctive Query
In database theory, a conjunctive query is a restricted form of first-order queries using the logical conjunction operator. Many first-order queries can be written as conjunctive queries. In particular, a large part of queries issued on relational databases can be expressed in this way. Conjunctive queries also have a number of desirable theoretical properties that larger classes of queries (e.g., the relational algebra queries) do not share. Definition The conjunctive queries are the fragment of (domain independent) first-order logic given by the set of formulae that can be constructed from atomic formulae using conjunction ∧ and existential quantification ∃, but not using disjunction ∨, negation ¬, or universal quantification ∀. Each such formula can be rewritten (efficiently) into an equivalent formula in prenex normal form, thus this form is usually simply assumed. Thus conjunctive queries are of the following general form: :(x_1, \ldots, x_k).\exists x_, \ldo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |