|
Butcher Series
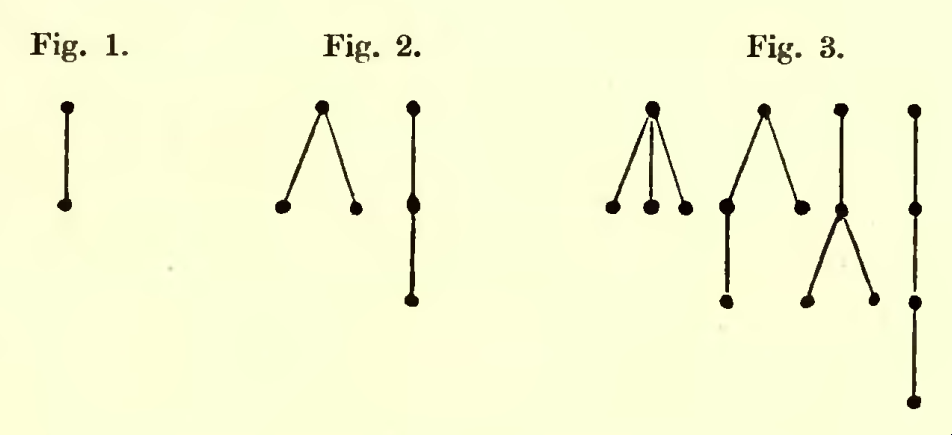
In mathematics, the Butcher group, named after the New Zealand mathematician John C. Butcher by , is an infinite-dimensional Lie group first introduced in numerical analysis to study solutions of non-linear ordinary differential equations by the Runge–Kutta method. It arose from an algebraic formalism involving rooted trees that provides formal power series solutions of the differential equation modeling the flow of a vector field. It was , prompted by the work of Sylvester on change of variables in differential calculus, who first noted that the derivatives of a composition of functions can be conveniently expressed in terms of rooted trees and their combinatorics. pointed out that the Butcher group is the group of characters of the Hopf algebra of rooted trees that had arisen independently in their own work on renormalization in quantum field theory and Connes' work with Moscovici on local index theorems. This Hopf algebra, often called the ''Connes–Kreimer alge ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Index Theorem
Index (: indexes or indices) may refer to: Arts, entertainment, and media Fictional entities * Index (''A Certain Magical Index''), a character in the light novel series ''A Certain Magical Index'' * The Index, an item on the Halo Array in the ''Halo'' video game series Periodicals and news portals * ''Index Magazine'', a publication for art and culture * Index.hr, a Croatian online newspaper * index.hu, a Hungarian-language news and community portal * ''The Index'' (Kalamazoo College), a student newspaper * ''The Index'', an 1860s European propaganda journal created by Henry Hotze to support the Confederate States of America * ''Truman State University Index'', a student newspaper Other arts, entertainment and media * The Index (band) * ''Indexed'', a Web cartoon by Jessica Hagy * ''Index'', album by Ana Mena Business enterprises and events * Index (retailer), a former UK catalogue retailer * INDEX, a market research fair in Lucknow, India * Index Corporation, a Japanese v ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Antipode (algebra)
In mathematics, a Hopf algebra, named after Heinz Hopf, is a structure that is simultaneously a ( unital associative) algebra and a (counital coassociative) coalgebra, with these structures' compatibility making it a bialgebra, and that moreover is equipped with an antihomomorphism satisfying a certain property. The representation theory of a Hopf algebra is particularly nice, since the existence of compatible comultiplication, counit, and antipode allows for the construction of tensor products of representations, trivial representations, and dual representations. Hopf algebras occur naturally in algebraic topology, where they originated and are related to the H-space concept, in group scheme theory, in group theory (via the concept of a group ring), and in numerous other places, making them probably the most familiar type of bialgebra. Hopf algebras are also studied in their own right, with much work on specific classes of examples on the one hand and classification problems on t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |