|
Brittle System
Brittle systems theory creates an analogy between communication theory and mechanical systems. A brittle system is a system characterized by a sudden and steep decline in performance as the system state changes. This can be due to input parameters that exceed a specified input, or environmental conditions that exceed specified operating boundaries. This is the opposite of a gracefully degrading system. Brittle system analysis develops an analogy with materials science in order to analyze system brittleness.Stephen F. Bush, John Hershey and Kirby Vosburgh, Brittle System Analysis, A system that is brittle (but initially robust enough to gain at least some foothold in the marketplace) will tend to operate with acceptable performance until it reaches a limit and then degrade suddenly and catastrophically. The table below illustrates the concept behind the analysis using an example of a communication system. See also * Reliability engineering * Catastrophe theory In mathemati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stress (mechanics)
In continuum mechanics, stress is a physical quantity. It is a quantity that describes the magnitude of forces that cause deformation. Stress is defined as ''force per unit area''. When an object is pulled apart by a force it will cause elongation which is also known as deformation, like the stretching of an elastic band, it is called tensile stress. But, when the forces result in the compression of an object, it is called compressive stress. It results when forces like tension or compression act on a body. The greater this force and the smaller the cross-sectional area of the body on which it acts, the greater the stress. Therefore, stress is measured in newton per square meter (N/m2) or pascal (Pa). Stress expresses the internal forces that neighbouring particles of a continuous material exert on each other, while strain is the measure of the deformation of the material. For example, when a solid vertical bar is supporting an overhead weight, each particle in the bar pu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Toughness
In materials science and metallurgy, toughness is the ability of a material to absorb energy and plastically deform without fracturing."Toughness" Brian Larson, editor, 2001–2011, The Collaboration for NDT Education, Iowa State University [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hardness
In materials science, hardness (antonym: softness) is a measure of the resistance to localized plastic deformation induced by either mechanical indentation or abrasion (mechanical), abrasion. In general, different materials differ in their hardness; for example hard metals such as titanium and beryllium are harder than soft metals such as sodium and metallic tin, or wood and common plastics. Macroscopic hardness is generally characterized by strong intermolecular bonds, but the behavior of solid materials under force is complex; therefore, hardness can be measured in different ways, such as scratch hardness, indentation hardness, and rebound hardness. Hardness is dependent on ductility, elasticity (physics), elastic stiffness, plasticity (physics), plasticity, deformation (mechanics), strain, strength of materials, strength, toughness, viscoelasticity, and viscosity. Common examples of hard matter are ceramics, concrete, certain metals, and superhard materials, which can be cont ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ductility
Ductility is a mechanical property commonly described as a material's amenability to drawing (e.g. into wire). In materials science, ductility is defined by the degree to which a material can sustain plastic deformation under tensile stress before failure. Ductility is an important consideration in engineering and manufacturing. It defines a material's suitability for certain manufacturing operations (such as cold working) and its capacity to absorb mechanical overload.. Some metals that are generally described as ductile include gold and copper. However, not all metals experience ductile failure as some can be characterized with brittle failure like cast iron. Polymers generally can be viewed as ductile materials as they typically allow for plastic deformation. Malleability, a similar mechanical property, is characterized by a material's ability to deform plastically without failure under compressive stress. Historically, materials were considered malleable if they wer ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elastic And Plastic Strain
In physics and materials science, plasticity, also known as plastic deformation, is the ability of a solid material to undergo permanent deformation, a non-reversible change of shape in response to applied forces. For example, a solid piece of metal being bent or pounded into a new shape displays plasticity as permanent changes occur within the material itself. In engineering, the transition from elastic behavior to plastic behavior is known as yielding. Plastic deformation is observed in most materials, particularly metals, soils, rocks, concrete, and foams. However, the physical mechanisms that cause plastic deformation can vary widely. At a crystalline scale, plasticity in metals is usually a consequence of dislocations. Such defects are relatively rare in most crystalline materials, but are numerous in some and part of their crystal structure; in such cases, plastic crystallinity can result. In brittle materials such as rock, concrete and bone, plasticity is caused p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fracture
Fracture is the separation of an object or material into two or more pieces under the action of stress. The fracture of a solid usually occurs due to the development of certain displacement discontinuity surfaces within the solid. If a displacement develops perpendicular to the surface, it is called a normal tensile crack or simply a crack; if a displacement develops tangentially, it is called a shear crack, slip band or dislocation. Fracture#Brittle, Brittle fractures occur with no apparent deformation before fracture. Fracture#Ductile, Ductile fractures occur after visible deformation. Fracture strength, or breaking strength, is the stress when a specimen fails or fractures. The detailed understanding of how a fracture occurs and develops in materials is the object of fracture mechanics. Strength Fracture strength, also known as breaking strength, is the stress at which a specimen Structural integrity and failure, fails via fracture. This is usually determined for a gi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Brittleness
A material is brittle if, when subjected to stress, it fractures with little elastic deformation and without significant plastic deformation. Brittle materials absorb relatively little energy prior to fracture, even those of high strength. Breaking is often accompanied by a sharp snapping sound. When used in materials science, it is generally applied to materials that fail when there is little or no plastic deformation before failure. One proof is to match the broken halves, which should fit exactly since no plastic deformation has occurred. Brittleness in different materials Polymers Mechanical characteristics of polymers can be sensitive to temperature changes near room temperatures. For example, poly(methyl methacrylate) is extremely brittle at temperature 4˚C, but experiences increased ductility with increased temperature. Amorphous polymers are polymers that can behave differently at different temperatures. They may behave like a glass at low temperatures (the gla ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Deformation (engineering)
In engineering, deformation refers to the change in size or shape of an object. ''Displacements'' are the ''absolute'' change in position of a point on the object. Deflection is the relative change in external displacements on an object. Strain is the ''relative'' internal change in shape of an infinitesimally small cube of material and can be expressed as a non-dimensional change in length or angle of distortion of the cube. Strains are related to the forces acting on the cube, which are known as stress, by a stress-strain curve. The relationship between stress and strain is generally linear and reversible up until the yield point and the deformation is elastic. The linear relationship for a material is known as Young's modulus. Above the yield point, some degree of permanent distortion remains after unloading and is termed plastic deformation. The determination of the stress and strain throughout a solid object is given by the field of strength of materials and for a s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
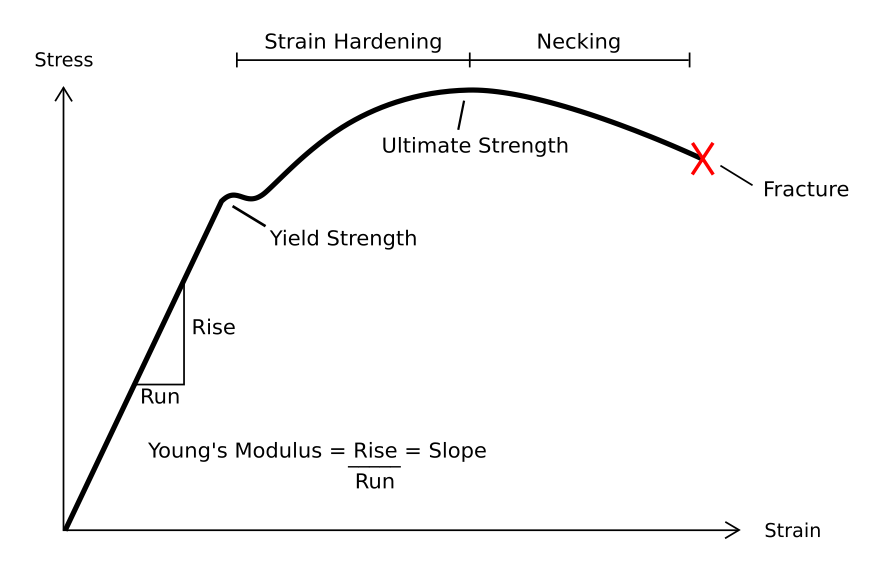
Young's Modulus
Young's modulus E, the Young modulus, or the modulus of elasticity in tension or compression (i.e., negative tension), is a mechanical property that measures the tensile or compressive stiffness of a solid material when the force is applied lengthwise. It quantifies the relationship between tensile/compressive stress \sigma (force per unit area) and axial strain \varepsilon (proportional deformation) in the linear elastic region of a material and is determined using the formula: E = \frac Young's moduli are typically so large that they are expressed not in pascals but in gigapascals (GPa). Example: * Silly Putty (increasing pressure: length increases quickly, meaning tiny E) * Aluminum (increasing pressure: length increases slowly, meaning high E) Higher Young's modulus corresponds to greater (lengthwise) stiffness. Although Young's modulus is named after the 19th-century British scientist Thomas Young, the concept was developed in 1727 by Leonhard Euler. The first ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Reliability Engineering
Reliability engineering is a sub-discipline of systems engineering that emphasizes the ability of equipment to function without failure. Reliability describes the ability of a system or component to function under stated conditions for a specified period of time. Reliability is closely related to availability, which is typically described as the ability of a component or system to function at a specified moment or interval of time. The reliability function is theoretically defined as the probability of success at time t, which is denoted R(t). This probability is estimated from detailed (physics of failure) analysis, previous data sets or through reliability testing and reliability modelling. Availability, testability, maintainability and maintenance are often defined as a part of "reliability engineering" in reliability programs. Reliability often plays the key role in the cost-effectiveness of systems. Reliability engineering deals with the prediction, prevention and man ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Catastrophe Theory
In mathematics, catastrophe theory is a branch of bifurcation theory in the study of dynamical systems; it is also a particular special case of more general singularity theory in geometry. Bifurcation theory studies and classifies phenomena characterized by sudden shifts in behavior arising from small changes in circumstances, analysing how the qualitative nature of equation solutions depends on the parameters that appear in the equation. This may lead to sudden and dramatic changes, for example the unpredictable timing and magnitude of a landslide. Catastrophe theory originated with the work of the French mathematician René Thom in the 1960s, and became very popular due to the efforts of Christopher Zeeman in the 1970s. It considers the special case where the long-run stable equilibrium can be identified as the minimum of a smooth, well-defined potential function ( Lyapunov function). In the late 1970s, applications of catastrophe theory to areas outside its scope began ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |