|
Biorthogonal Nearly Coiflet Basis
In applied mathematics, biorthogonal nearly coiflet bases are wavelet bases proposed by Lowell L. Winger. The wavelet is based on biorthogonal coiflet wavelet bases, but sacrifices its regularity to increase the filter's bandwidth, which might lead to better image compression performance. Motivation Nowadays, a large amount of information is stored, processed, and delivered, so the method of data compressing — especially for images — becomes more significant. Since wavelet transforms can deal with signals in both space and frequency domains, they compensate for the deficiency of Fourier transforms and emerged as a potential technique for image processing. Traditional wavelet filter design prefers filters with high regularity and smoothness to perform image compression. Coiflets are such a kind of filter which emphasizes the vanishing moments of both the wavelet and scaling function, and can be achieved by maximizing the total number of vanishing moments and distributing t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Applied Mathematics
Applied mathematics is the application of mathematical methods by different fields such as physics, engineering, medicine, biology, finance, business, computer science, and industry. Thus, applied mathematics is a combination of mathematical science and specialized knowledge. The term "applied mathematics" also describes the professional specialty in which mathematicians work on practical problems by formulating and studying mathematical models. In the past, practical applications have motivated the development of mathematical theories, which then became the subject of study in pure mathematics where abstract concepts are studied for their own sake. The activity of applied mathematics is thus intimately connected with research in pure mathematics. History Historically, applied mathematics consisted principally of applied analysis, most notably differential equations; approximation theory (broadly construed, to include representations, asymptotic methods, variation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Biorthogonal Wavelet
A Biorthogonal wavelet is a wavelet where the associated wavelet transform is invertible but not necessarily orthogonal In mathematics, orthogonality is the generalization of the geometric notion of '' perpendicularity''. By extension, orthogonality is also used to refer to the separation of specific features of a system. The term also has specialized meanings in .... Designing biorthogonal wavelets allows more degrees of freedom than orthogonal wavelets. One additional degree of freedom is the possibility to construct symmetric wavelet functions. In the biorthogonal case, there are two scaling functions \phi,\tilde\phi, which may generate different multiresolution analyses, and accordingly two different wavelet functions \psi,\tilde\psi. So the numbers ''M'' and ''N'' of coefficients in the scaling sequences a,\tilde a may differ. The scaling sequences must satisfy the following biorthogonality condition :\sum_ a_n \tilde a_=2\cdot\delta_. Then the wavelet sequences can be de ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Degrees Of Freedom
Degrees of freedom (often abbreviated df or DOF) refers to the number of independent variables or parameters of a thermodynamic system. In various scientific fields, the word "freedom" is used to describe the limits to which physical movement or other physical processes are possible. This relates to the philosophical concept to the extent that people may be considered to have as much freedom as they are physically able to exercise. Applications Statistics In statistics, degrees of freedom refers to the number of variables in a statistic calculation that can vary. It can be calculated by subtracting the number of estimated parameters from the total number of values in the sample. For example, a sample variance calculation based on n samples will have n-1 degrees of freedom, because sample variance is calculated using the sample mean as an estimate of the actual mean. Mathematics In mathematics Mathematics is an area of knowledge that includes the topics of numbers, for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Closed-form Expression
In mathematics, a closed-form expression is a mathematical expression that uses a finite number of standard operations. It may contain constants, variables, certain well-known operations (e.g., + − × ÷), and functions (e.g., ''n''th root, exponent, logarithm, trigonometric functions, and inverse hyperbolic functions), but usually no limit, differentiation, or integration. The set of operations and functions may vary with author and context. Example: roots of polynomials The solutions of any quadratic equation with complex coefficients can be expressed in closed form in terms of addition, subtraction, multiplication, division, and square root extraction, each of which is an elementary function. For example, the quadratic equation :ax^2+bx+c=0, is tractable since its solutions can be expressed as a closed-form expression, i.e. in terms of elementary functions: :x=\frac. Similarly, solutions of cubic and quartic (third and fourth degree) equations can be ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
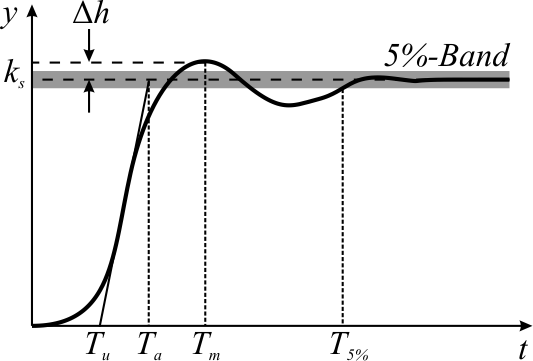
Overshoot (signal)
In signal processing, control theory, electronics, and mathematics, overshoot is the occurrence of a signal or function exceeding its target. Undershoot is the same phenomenon in the opposite direction. It arises especially in the step response of bandlimited systems such as low-pass filters. It is often followed by ringing, and at times conflated with the latter. Definition Maximum overshoot is defined in Katsuhiko Ogata's ''Discrete-time control systems'' as "the maximum peak value of the response curve measured from the desired response of the system." Control theory In control theory, overshoot refers to an output exceeding its final, steady-state value. For a step input, the ''percentage overshoot'' (PO) is the maximum value minus the step value divided by the step value. In the case of the unit step, the ''overshoot'' is just the maximum value of the step response minus one. Also see the definition of ''overshoot'' in an electronics context. For second-order sys ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
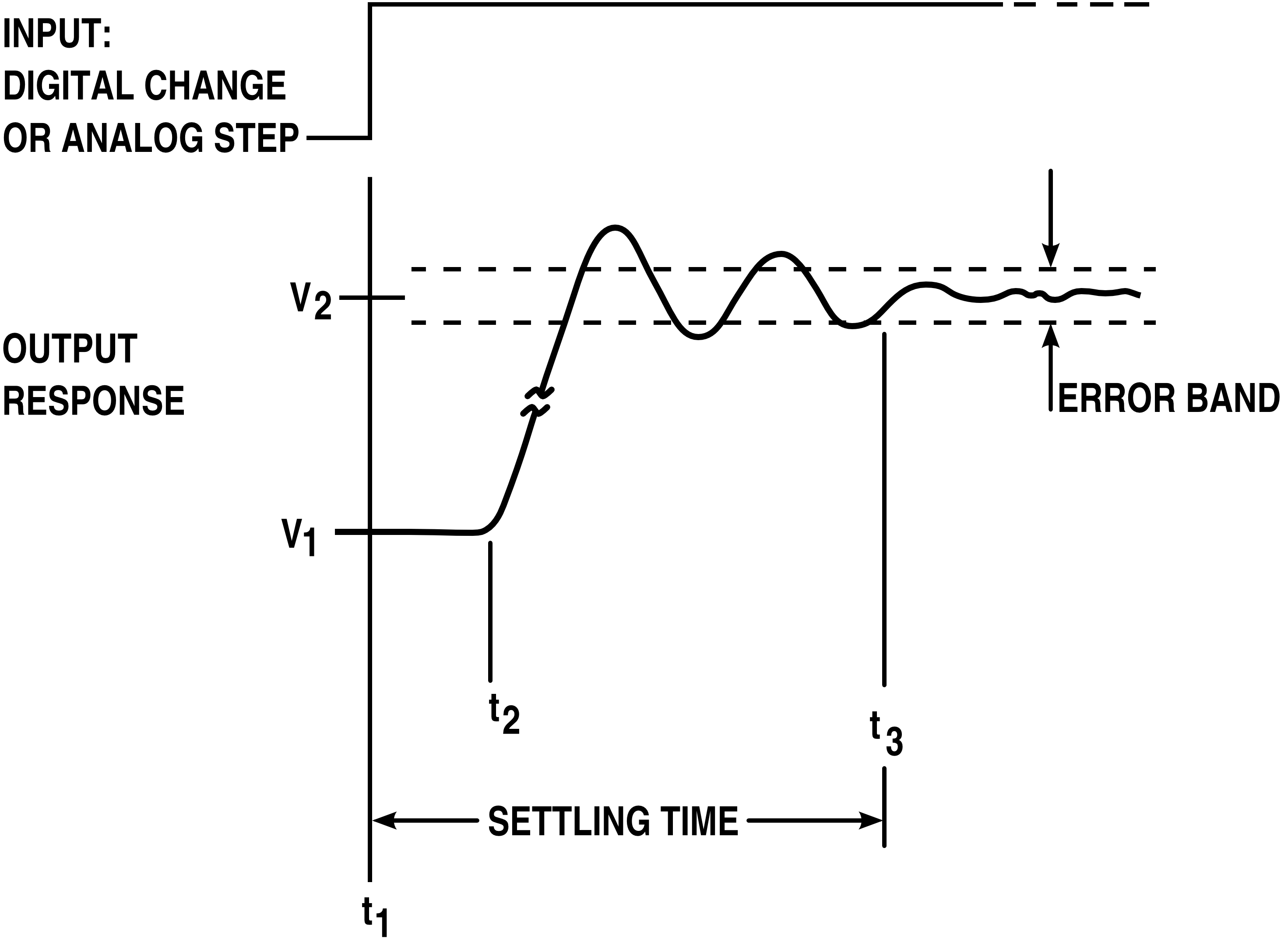
Ringing (signal)
In electronics, signal processing, and video, ringing is oscillation of a signal, particularly in the step response (the response to a sudden change in input). Often ringing is undesirable, but not always, as in the case of resonant inductive coupling. It is also known as hunting. It is closely related to overshoot, often instigated as damping response following overshoot or undershoot, and thus the terms are at times conflated. It is also known as ripple, particularly in electricity or in frequency domain response. Electricity In electrical circuits, ringing is an unwanted oscillation of a voltage or current. It happens when an electrical pulse causes the parasitic capacitances and inductances in the circuit (i.e. those that are not part of the design, but just by-products of the materials used to construct the circuit) to resonate at their characteristic frequency.Johnson, H. and Graham, M. ''High-Speed Digital Design: A Handbook of Black Magic''. 1993. pp. 88–90 Rin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Passband
A passband is the range of frequencies or wavelengths that can pass through a filter. For example, a radio receiver contains a bandpass filter to select the frequency of the desired radio signal out of all the radio waves picked up by its antenna. The passband of a receiver is the range of frequencies it can receive when it is tuned into the desired frequency (channel). A bandpass-filtered signal (that is, a signal with energy only in a passband), is known as a bandpass signal, in contrast to a baseband signal. Filters In telecommunications, optics, and acoustics, a passband (a band-pass filtered signal) is the portion of the frequency spectrum that is transmitted (with minimum relative loss or maximum relative gain) by some filtering device. In other words, it is a ''band'' of frequencies which ''pass''es through some filter or a set of filters. The accompanying figure shows a schematic of a waveform being filtered by a bandpass filter consisting of a highpass an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coefficient
In mathematics, a coefficient is a multiplicative factor in some term of a polynomial, a series, or an expression; it is usually a number, but may be any expression (including variables such as , and ). When the coefficients are themselves variables, they may also be called parameters. For example, the polynomial 2x^2-x+3 has coefficients 2, −1, and 3, and the powers of the variable x in the polynomial ax^2+bx+c have coefficient parameters a, b, and c. The constant coefficient is the coefficient not attached to variables in an expression. For example, the constant coefficients of the expressions above are the number 3 and the parameter ''c'', respectively. The coefficient attached to the highest degree of the variable in a polynomial is referred to as the leading coefficient. For example, in the expressions above, the leading coefficients are 2 and ''a'', respectively. Terminology and definition In mathematics, a coefficient is a multiplicative factor in some ter ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polynomial
In mathematics, a polynomial is an expression consisting of indeterminates (also called variables) and coefficients, that involves only the operations of addition, subtraction, multiplication, and positive-integer powers of variables. An example of a polynomial of a single indeterminate is . An example with three indeterminates is . Polynomials appear in many areas of mathematics and science. For example, they are used to form polynomial equations, which encode a wide range of problems, from elementary word problems to complicated scientific problems; they are used to define polynomial functions, which appear in settings ranging from basic chemistry and physics to economics and social science; they are used in calculus and numerical analysis to approximate other functions. In advanced mathematics, polynomials are used to construct polynomial rings and algebraic varieties, which are central concepts in algebra and algebraic geometry. Etymology The word ''polynomial'' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bernstein Polynomial
In the mathematical field of numerical analysis, a Bernstein polynomial is a polynomial that is a linear combination of Bernstein basis polynomials. The idea is named after Sergei Natanovich Bernstein. A numerically stable way to evaluate polynomials in Bernstein form is de Casteljau's algorithm. Polynomials in Bernstein form were first used by Bernstein in a constructive proof for the Weierstrass approximation theorem. With the advent of computer graphics, Bernstein polynomials, restricted to the interval , 1 became important in the form of Bézier curves. Definition The ''n''+1 Bernstein basis polynomials of degree ''n'' are defined as : b_(x) = \binom x^ \left( 1 - x \right)^, \quad \nu = 0, \ldots, n, where \tbinom is a binomial coefficient. So, for example, b_(x) = \tbinomx^2(1-x)^3 = 10x^2(1-x)^3. The first few Bernstein basis polynomials for blending 1, 2, 3 or 4 values together are: : \begin b_(x) & = 1, \\ b_(x) & = 1 - x, & b_(x) & = x \\ b_(x) & ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Smoothness
In mathematical analysis, the smoothness of a function is a property measured by the number of continuous derivatives it has over some domain, called ''differentiability class''. At the very minimum, a function could be considered smooth if it is differentiable everywhere (hence continuous). At the other end, it might also possess derivatives of all orders in its domain, in which case it is said to be infinitely differentiable and referred to as a C-infinity function (or C^ function). Differentiability classes Differentiability class is a classification of functions according to the properties of their derivatives. It is a measure of the highest order of derivative that exists and is continuous for a function. Consider an open set U on the real line and a function f defined on U with real values. Let ''k'' be a non-negative integer. The function f is said to be of differentiability class ''C^k'' if the derivatives f',f'',\dots,f^ exist and are continuous on U. If f is k-dif ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orthogonality
In mathematics, orthogonality is the generalization of the geometric notion of '' perpendicularity''. By extension, orthogonality is also used to refer to the separation of specific features of a system. The term also has specialized meanings in other fields including art and chemistry. Etymology The word comes from the Ancient Greek ('), meaning "upright", and ('), meaning "angle". The Ancient Greek (') and Classical Latin ' originally denoted a rectangle. Later, they came to mean a right triangle. In the 12th century, the post-classical Latin word ''orthogonalis'' came to mean a right angle or something related to a right angle. Mathematics Physics * In optics, polarization states are said to be orthogonal when they propagate independently of each other, as in vertical and horizontal linear polarization or right- and left-handed circular polarization. * In special relativity, a time axis determined by a rapidity of motion is hyperbolic-orthogonal to a space axis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |