|
Bell Diagonal State
Bell diagonal states are a class of bipartite qubit states that are frequently used in quantum information and quantum computation theory. Definition The Bell diagonal state is defined as the probabilistic mixture of Bell states: : , \phi^+\rangle = \frac (, 0\rangle_A \otimes , 0\rangle_B + , 1\rangle_A \otimes , 1\rangle_B) : , \phi^-\rangle = \frac (, 0\rangle_A \otimes , 0\rangle_B - , 1\rangle_A \otimes , 1\rangle_B) : , \psi^+\rangle = \frac (, 0\rangle_A \otimes , 1\rangle_B + , 1\rangle_A \otimes , 0\rangle_B) : , \psi^-\rangle = \frac (, 0\rangle_A \otimes , 1\rangle_B - , 1\rangle_A \otimes , 0\rangle_B) In density operator form, a Bell diagonal state is defined as \varrho^=p_1, \phi^+\rangle \langle \phi^+, +p_2, \phi^-\rangle\langle \phi^-, +p_3, \psi^+\rangle\langle \psi^+, +p_4, \psi^-\rangle\langle\psi^-, where p_1,p_2,p_3,p_4 is a probability distribution. Since p_1+p_2+p_3+p_4=1, a Bell diagonal state is determined by three real parameters. The maximum pro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
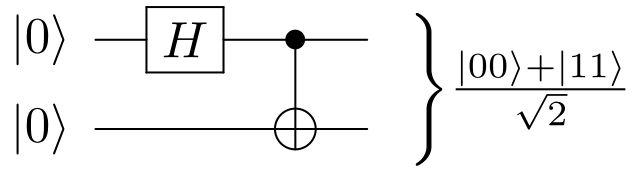
Bell State
In quantum information science, the Bell's states or EPR pairs are specific quantum states of two qubits that represent the simplest examples of quantum entanglement. The Bell's states are a form of entangled and normalized basis vectors. This normalization implies that the overall probability of the particles being in one of the mentioned states is 1: \langle \Phi, \Phi \rangle = 1. Entanglement is a basis-independent result of superposition. Due to this superposition, measurement of the qubit will " collapse" it into one of its basis states with a given probability. Because of the entanglement, measurement of one qubit will "collapse" the other qubit to a state whose measurement will yield one of two possible values, where the value depends on which Bell's state the two qubits are in initially. Bell's states can be generalized to certain quantum states of multi-qubit systems, such as the GHZ state for three or more subsystems. Understanding of Bell's states is useful in a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Separable State
In quantum mechanics, separable states are multipartite quantum states that can be written as a convex combination of product states. Product states are multipartite quantum states that can be written as a tensor product of states in each space. The physical intuition behind these definitions is that product states have no correlation between the different degrees of freedom, while separable states might have correlations, but all such correlations can be explained as due to a classical random variable, as opposed to being due to entanglement. In the special case of pure states the definition simplifies: a pure state is separable if and only if it is a product state. A state is said to be entangled if it is not separable. In general, determining if a state is separable is not straightforward and the problem is classed as NP-hard. Separability of bipartite systems Consider first composite states with two degrees of freedom, referred to as ''bipartite states''. By a postulate ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Entanglement
Quantum entanglement is the phenomenon where the quantum state of each Subatomic particle, particle in a group cannot be described independently of the state of the others, even when the particles are separated by a large distance. The topic of quantum entanglement is at the heart of the disparity between classical physics and quantum physics: entanglement is a primary feature of quantum mechanics not present in classical mechanics. Measurement#Quantum mechanics, Measurements of physical properties such as position (vector), position, momentum, Spin (physics), spin, and polarization (waves), polarization performed on entangled particles can, in some cases, be found to be perfectly correlated. For example, if a pair of entangled particles is generated such that their total spin is known to be zero, and one particle is found to have clockwise spin on a first axis, then the spin of the other particle, measured on the same axis, is found to be anticlockwise. However, this behavior ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Relative Entropy
In quantum information theory, quantum relative entropy is a measure of distinguishability between two quantum states. It is the quantum mechanical analog of relative entropy. Motivation For simplicity, it will be assumed that all objects in the article are finite-dimensional. We first discuss the classical case. Suppose the probabilities of a finite sequence of events is given by the probability distribution ''P'' = , but somehow we mistakenly assumed it to be ''Q'' = . For instance, we can mistake an unfair coin for a fair one. According to this erroneous assumption, our uncertainty about the ''j''-th event, or equivalently, the amount of information provided after observing the ''j''-th event, is :\; - \log q_j. The (assumed) average uncertainty of all possible events is then :\; - \sum_j p_j \log q_j. On the other hand, the Shannon entropy of the probability distribution ''p'', defined by :\; - \sum_j p_j \log p_j, is the real amount of uncertainty before observation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Binary Entropy Function
Binary may refer to: Science and technology Mathematics * Binary number, a representation of numbers using only two values (0 and 1) for each digit * Binary function, a function that takes two arguments * Binary operation, a mathematical operation that takes two arguments * Binary relation, a relation involving two elements * Finger binary, a system for counting in binary numbers on the fingers of human hands Computing * Binary code, the representation of text and data using only the digits 1 and 0 * Bit, or binary digit, the basic unit of information in computers * Binary file, composed of something other than human-readable text ** Executable, a type of binary file that contains machine code for the computer to execute * Binary tree, a computer tree data structure in which each node has at most two children * Binary-coded decimal, a method for encoding for decimal digits in binary sequences Astronomy * Binary star, a star system with two stars in it * Binary planet, t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Entanglement Of Formation
The entanglement of formation is a quantity that measures the entanglement of a bipartite quantum state. Definition For a pure bipartite quantum state , \psi\rangle_, using Schmidt decomposition, we see that the reduced density matrices of systems A and B, \rho_A and \rho_B, have the same spectrum. The von Neumann entropy S(\rho_A)=S(\rho_B) of the reduced density matrix can be used to measure the entanglement of the state , \psi\rangle_. We denote this kind of measure as E_(, \psi\rangle_)=S(\rho_A)=S(\rho_B) , and call it the entanglement entropy. This is also known as the entanglement of formation of a pure state. For a mixed bipartite state \rho_, a natural generalization is to consider all the ensemble realizations of the mixed state. We define the entanglement of formation for mixed states by minimizing over all these ensemble realizations, :E_f (\rho_)= \inf\left\ , where the infimum is taken over all the possible ways in which one can decompose \rho_ into pure states ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Negativity (quantum Mechanics)
In quantum mechanics, negativity is a measure of quantum entanglement which is easy to compute. It is a measure deriving from the PPT criterion for separability. It has been shown to be an entanglement monotone and hence a proper measure of entanglement. Definition The negativity of a subsystem A can be defined in terms of a density matrix \rho as: :\mathcal(\rho) \equiv \frac where: * \rho^ is the partial transpose of \rho with respect to subsystem A * , , X, , _1 = \text, X, = \text \sqrt is the trace norm or the sum of the singular values of the operator X . An alternative and equivalent definition is the absolute sum of the negative eigenvalues of \rho^: : \mathcal(\rho) = \left, \sum_ \lambda_i \ = \sum_i \frac where \lambda_i are all of the eigenvalues. Properties * Is a convex function of \rho: :\mathcal(\sum_p_\rho_) \le \sum_p_\mathcal(\rho_) * Is an entanglement monotone: :\mathcal(P(\rho)) \le \mathcal(\rho) where P(\rho) is an arbitrary LOCC LOCC ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Reduced Density Matrix
Quantum entanglement is the phenomenon where the quantum state of each particle in a group cannot be described independently of the state of the others, even when the particles are separated by a large distance. The topic of quantum entanglement is at the heart of the disparity between classical physics and quantum physics: entanglement is a primary feature of quantum mechanics not present in classical mechanics. Measurements of physical properties such as position, momentum, spin, and polarization performed on entangled particles can, in some cases, be found to be perfectly correlated. For example, if a pair of entangled particles is generated such that their total spin is known to be zero, and one particle is found to have clockwise spin on a first axis, then the spin of the other particle, measured on the same axis, is found to be anticlockwise. However, this behavior gives rise to seemingly paradoxical effects: any measurement of a particle's properties results in an appar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Information Science
Quantum information science is a field that combines the principles of quantum mechanics with information theory to study the processing, analysis, and transmission of information. It covers both theoretical and experimental aspects of quantum physics, including the limits of what can be achieved with quantum information. The term quantum information theory is sometimes used, but it does not include experimental research and can be confused with a subfield of quantum information science that deals with the processing of quantum information. Scientific and engineering studies Quantum teleportation, Quantum entanglement, entanglement and the manufacturing of quantum computers depend on a comprehensive understanding of quantum physics and engineering. Google and IBM have invested significantly in quantum computer hardware research, leading to significant progress in manufacturing quantum computers since the 2010s. Currently, it is possible to create a quantum computer with over 100 qub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |