|
Automatic Differentiation
In mathematics and computer algebra, automatic differentiation (AD), also called algorithmic differentiation, computational differentiation, auto-differentiation, or simply autodiff, is a set of techniques to evaluate the derivative of a function specified by a computer program. AD exploits the fact that every computer program, no matter how complicated, executes a sequence of elementary arithmetic operations (addition, subtraction, multiplication, division, etc.) and elementary functions ( exp, log, sin, cos, etc.). By applying the chain rule repeatedly to these operations, derivatives of arbitrary order can be computed automatically, accurately to working precision, and using at most a small constant factor more arithmetic operations than the original program. Automatic differentiation is distinct from symbolic differentiation and numerical differentiation. Symbolic differentiation faces the difficulty of converting a computer program into a single mathematical expression an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Expression (mathematics)
In mathematics, an expression or mathematical expression is a finite combination of symbols that is well-formed according to rules that depend on the context. Mathematical symbols can designate numbers ( constants), variables, operations, functions, brackets, punctuation, and grouping to help determine order of operations and other aspects of logical syntax. Many authors distinguish an expression from a ''formula'', the former denoting a mathematical object, and the latter denoting a statement about mathematical objects. For example, 8x-5 is an expression, while 8x-5 \geq 5x-8 is a formula. However, in modern mathematics, and in particular in computer algebra, formulas are viewed as expressions that can be evaluated to ''true'' or ''false'', depending on the values that are given to the variables occurring in the expressions. For example 8x-5 \geq 5x-8 takes the value ''false'' if is given a value less than –1, and the value ''true'' otherwise. Examples The use of exp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Machine Learning
Machine learning (ML) is a field of inquiry devoted to understanding and building methods that 'learn', that is, methods that leverage data to improve performance on some set of tasks. It is seen as a part of artificial intelligence. Machine learning algorithms build a model based on sample data, known as training data, in order to make predictions or decisions without being explicitly programmed to do so. Machine learning algorithms are used in a wide variety of applications, such as in medicine, email filtering, speech recognition, agriculture, and computer vision, where it is difficult or unfeasible to develop conventional algorithms to perform the needed tasks.Hu, J.; Niu, H.; Carrasco, J.; Lennox, B.; Arvin, F.,Voronoi-Based Multi-Robot Autonomous Exploration in Unknown Environments via Deep Reinforcement Learning IEEE Transactions on Vehicular Technology, 2020. A subset of machine learning is closely related to computational statistics, which focuses on making predicti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
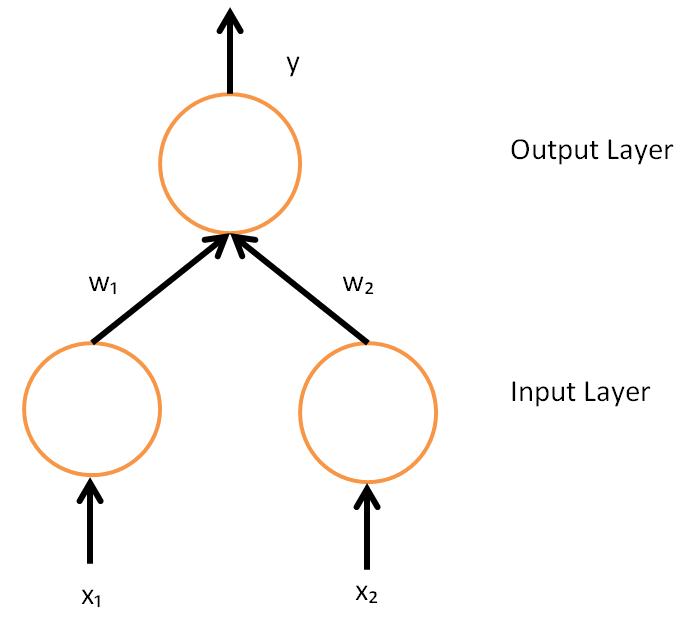
Backpropagation
In machine learning, backpropagation (backprop, BP) is a widely used algorithm for training feedforward artificial neural networks. Generalizations of backpropagation exist for other artificial neural networks (ANNs), and for functions generally. These classes of algorithms are all referred to generically as "backpropagation". In fitting a neural network, backpropagation computes the gradient of the loss function with respect to the weights of the network for a single input–output example, and does so efficiently, unlike a naive direct computation of the gradient with respect to each weight individually. This efficiency makes it feasible to use gradient methods for training multilayer networks, updating weights to minimize loss; gradient descent, or variants such as stochastic gradient descent, are commonly used. The backpropagation algorithm works by computing the gradient of the loss function with respect to each weight by the chain rule, computing the gradient one lay ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Seppo Linnainmaa
Seppo Ilmari Linnainmaa (born 28 September 1945) is a Finnish mathematician and computer scientist. He was born in Pori. In 1974 he obtained the first doctorate ever awarded in computer science at the University of Helsinki. In 1976, he became Assistant Professor. From 1984 to 1985 he was Visiting Professor at the University of Maryland, USA. From 1986 to 1989 he was Chairman of the Finnish Artificial Intelligence Society. From 1989 to 2007, he was Research Professor at the VTT Technical Research Centre of Finland. He retired in 2007. Explicit, efficient error backpropagation in arbitrary, discrete, possibly sparsely connected, neural networks-like networks was first described in a 1970 master's thesis (Linnainmaa, 1970, 1976), albeit without reference to NNs,Jürgen Schmidhuber, (2015)Who Invented Backpropagation?/ref> when Linnainmaa introduced the reverse mode of automatic differentiation (AD), in order to efficiently compute the derivative of a differentiable composite func ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Unary Operation
In mathematics, an unary operation is an operation with only one operand, i.e. a single input. This is in contrast to binary operations, which use two operands. An example is any function , where is a set. The function is a unary operation on . Common notations are prefix notation (e.g. ¬, −), postfix notation (e.g. factorial ), functional notation (e.g. or ), and superscripts (e.g. transpose ). Other notations exist as well, for example, in the case of the square root, a horizontal bar extending the square root sign over the argument can indicate the extent of the argument. Examples Unary negative and positive As unary operations have only one operand they are evaluated before other operations containing them. Here is an example using negation: :3 − −2 Here, the first '−' represents the binary subtraction operation, while the second '−' represents the unary negation of the 2 (or '−2' could be taken to mean the integer −2). Therefore, the expressi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Covector
In mathematics, a linear form (also known as a linear functional, a one-form, or a covector) is a linear map from a vector space to its field of scalars (often, the real numbers or the complex numbers). If is a vector space over a field , the set of all linear functionals from to is itself a vector space over with addition and scalar multiplication defined pointwise. This space is called the dual space of , or sometimes the algebraic dual space, when a topological dual space is also considered. It is often denoted , p. 19, §3.1 or, when the field is understood, V^*; other notations are also used, such as V', V^ or V^. When vectors are represented by column vectors (as is common when a basis is fixed), then linear functionals are represented as row vectors, and their values on specific vectors are given by matrix products (with the row vector on the left). Examples * The constant zero function, mapping every vector to zero, is trivially a linear functional. * Index ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Transpose
In linear algebra, the transpose of a matrix is an operator which flips a matrix over its diagonal; that is, it switches the row and column indices of the matrix by producing another matrix, often denoted by (among other notations). The transpose of a matrix was introduced in 1858 by the British mathematician Arthur Cayley. In the case of a logical matrix representing a binary relation R, the transpose corresponds to the converse relation RT. Transpose of a matrix Definition The transpose of a matrix , denoted by , , , A^, , , or , may be constructed by any one of the following methods: # Reflect over its main diagonal (which runs from top-left to bottom-right) to obtain #Write the rows of as the columns of #Write the columns of as the rows of Formally, the -th row, -th column element of is the -th row, -th column element of : :\left mathbf^\operatorname\right = \left mathbf\right. If is an matrix, then is an matrix. In the case of square matrices, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Checkpointing Scheme
Checkpointing schemes are scientific computing algorithms used in solving time dependent adjoint equations, as well as reverse mode automatic differentiation.D. K. Pradhan and N. H. Vaidya, "Roll-forward checkpointing scheme: a novel fault-tolerant architecture," in IEEE Transactions on Computers, vol. 43, no. 10, pp. 1163-1174, Oct. 1994, doi: 10.1109/12.324542. References Bibliography * {{Cite book , last = Griewank , first = Andreas , title = Evaluating Derivatives: Principles and Techniques of Algorithmic Differentiation , publisher = SIAM Thailand ( ), historically known as Siam () and officially the Kingdom of Thailand, is a country in Southeast Asia, located at the centre of the Indochinese Peninsula, spanning , with a population of almost 70 million. The country is bo ... , series = Frontiers in Applied Mathematics , volume = 19 , year = 2000 , isbn = 0-89871-451-6 Differential calculus ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rematerialization
In computer science, rematerialization or remat is a compiler optimization which saves time by recomputing a value instead of loading it from memory. It is typically tightly integrated with register allocation, where it is used as an alternative to spilling registers to memory. It was conceived by Gregory Chaitin, Marc Auslander, Ashok Chandra, John Cocke, Martin Hopkins and Peter Markstein and implemented in the Pl.8 compiler for the 801 Minicomputer in the late 1970s. Later improvements were made by Preston Briggs, Keith D. Cooper, and Linda Torczon in 1992. Traditional optimizations such as common subexpression elimination and loop invariant hoisting often focus on eliminating redundant computation. Since computation requires CPU cycles, this is usually a good thing, but it has the potentially devastating side effect that it can increase the live ranges of variables and create many new variables, resulting in spills during register allocation. Rematerialization is ne ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Space–time Tradeoff
A space–time trade-off or time–memory trade-off in computer science is a case where an algorithm or program trades increased space usage with decreased time. Here, ''space'' refers to the data storage consumed in performing a given task (RAM, HDD, etc), and ''time'' refers to the time consumed in performing a given task (computation time or response time). The utility of a given space–time tradeoff is affected by related fixed and variable costs (of, e.g., CPU speed, storage space), and is subject to diminishing returns. History Biological usage of time–memory tradeoffs can be seen in the earlier stages of animal behavior. Using stored knowledge or encoding stimuli reactions as "instincts" in the DNA avoids the need for "calculation" in time-critical situations. More specific to computers, look-up tables have been implemented since the very earliest operating systems. In 1980 Martin Hellman first proposed using a time–memory tradeoff for cryptanalysis. Types of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
