|
Archimedes
Archimedes of Syracuse ( ; ) was an Ancient Greece, Ancient Greek Greek mathematics, mathematician, physicist, engineer, astronomer, and Invention, inventor from the ancient city of Syracuse, Sicily, Syracuse in History of Greek and Hellenistic Sicily, Sicily. Although few details of his life are known, based on his surviving work, he is considered one of the leading scientists in classical antiquity, and one of the greatest mathematicians of all time. Archimedes anticipated modern calculus and mathematical analysis, analysis by applying the concept of the Cavalieri's principle, infinitesimals and the method of exhaustion to derive and rigorously prove many geometry, geometrical theorem, theorems, including the area of a circle, the surface area and volume of a sphere, the area of an ellipse, the area under a parabola, the volume of a segment of a paraboloid of revolution, the volume of a segment of a hyperboloid of revolution, and the area of a spiral. Archimedes' other math ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Archimedes' Screw
The Archimedes' screw, also known as the Archimedean screw, hydrodynamic screw, water screw or Egyptian screw, is one of the earliest documented hydraulic machines. It was so-named after the Greek mathematician Archimedes who first described it around 234 BC, although the device had been developed in Egypt earlier in the century. It is a reversible hydraulic machine that can be operated both as a pump or a power generator. As a machine used for lifting water from a low-lying body of water into irrigation ditches, water is lifted by turning a screw-shaped surface inside a pipe. In the modern world, Archimedes screw pumps are widely used in wastewater treatment plants and for dewatering low-lying regions. Run in reverse, Archimedes screw turbines act as a new form of small hydroelectric powerplant that can be applied even in low head sites. Such generators operate in a wide range of flows (0.01 m^3/s to 14.5 m^3/s) and heads (0.1 m to 10 m), including low heads and moderate flow ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
List Of Things Named After Archimedes
Archimedes (c. 287 BC – c. 212 BC) is the eponym of all of the things (and topics) listed below. Mathematical concepts * Archimedean absolute value * Archimedean circle * Archimedean copula *Archimedean group *Archimedean ordered field * Archimedean point *Archimedean property *Archimedean solid *Archimedean spiral * Archimedean tiling * Archimedes' axiom * Archimedes' cattle problem * Archimedes' hat-box theorem * Archimedes constant *Archimedes number * Archimedes' quadruplets * Archimedes Square * Archimedes' twin circles * Heron–Archimedes formula * Non-Archimedean geometry *Non-Archimedean ordered field * Archimedes' ostomachion Physical concepts * Archimedes paradox * Archimedes' principle Technology Things invented by Archimedes * Archimedes' pulley *Archimedes' screw ** Archimedean turbine * Archimedes' heat ray * Claw of Archimedes * Trammel of Archimedes Other * Archimedes bridge * Archimede combined cycle power plant * SS Archimedes * Archimedes Grou ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
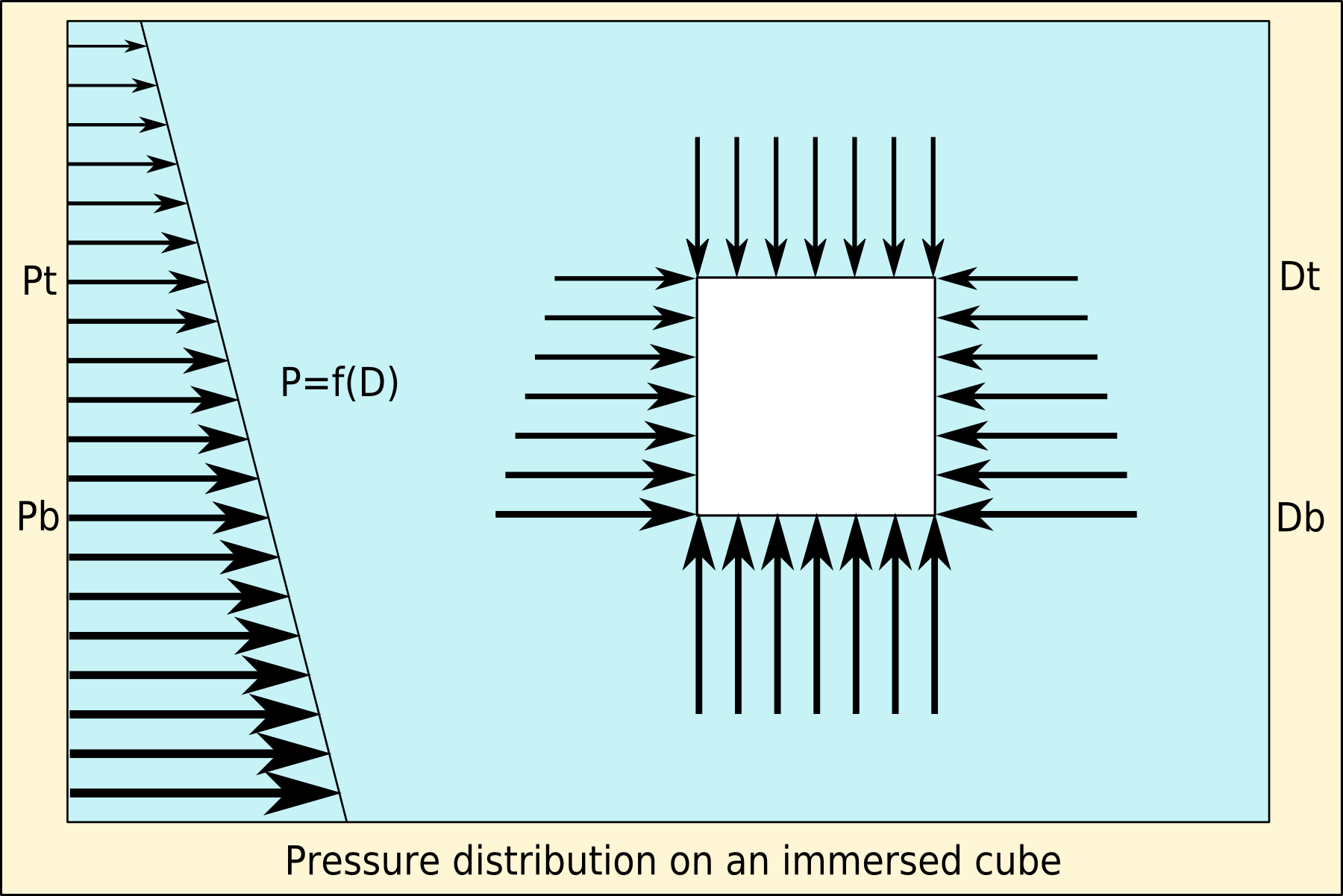
Archimedes' Principle
Archimedes' principle states that the upward buoyant force that is exerted on a body immersed in a fluid, whether fully or partially, is equal to the weight of the fluid that the body displaces. Archimedes' principle is a law of physics fundamental to fluid mechanics. It was formulated by Archimedes of Syracuse. Explanation In '' On Floating Bodies'', Archimedes suggested that (c. 246 BC): Archimedes' principle allows the buoyancy of any floating object partially or fully immersed in a fluid to be calculated. The downward force on the object is simply its weight. The upward, or buoyant, force on the object is that stated by Archimedes' principle above. Thus, the net force on the object is the difference between the magnitudes of the buoyant force and its weight. If this net force is positive, the object rises; if negative, the object sinks; and if zero, the object is neutrally buoyant—that is, it remains in place without either rising or sinking. In simple words, Archim ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Archimedes' Use Of Infinitesimals
''The Method of Mechanical Theorems'' (), also referred to as ''The Method'', is one of the major surviving works of the ancient Greek polymath Archimedes. ''The Method'' takes the form of a letter from Archimedes to Eratosthenes, the chief librarian at the Library of Alexandria, and contains the first attested explicit use of indivisibles (indivisibles are geometric versions of infinitesimals). The work was originally thought to be lost, but in 1906 was rediscovered in the celebrated Archimedes Palimpsest. The palimpsest includes Archimedes' account of the "mechanical method", so called because it relies on the center of weights of figures (centroid) and the law of the lever, which were demonstrated by Archimedes in ''On the Equilibrium of Planes''. Archimedes did not admit the method of indivisibles as part of rigorous mathematics, and therefore did not publish his method in the formal treatises that contain the results. In these treatises, he proves the same theorems by ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Greek Mathematics
Ancient Greek mathematics refers to the history of mathematical ideas and texts in Ancient Greece during Classical antiquity, classical and late antiquity, mostly from the 5th century BC to the 6th century AD. Greek mathematicians lived in cities spread around the shores of the ancient Mediterranean, from Anatolia to Italy and North Africa, but were united by Greek culture and the Ancient Greek, Greek language. The development of mathematics as a theoretical discipline and the use of deductive reasoning in Mathematical proof, proofs is an important difference between Greek mathematics and those of preceding civilizations. The early history of Greek mathematics is obscure, and traditional narratives of Theorem, mathematical theorems found before the fifth century BC are regarded as later inventions. It is now generally accepted that treatises of deductive mathematics written in Greek began circulating around the mid-fifth century BC, but the earliest complete work on the subje ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Area Of A Circle
In geometry, the area enclosed by a circle of radius is . Here, the Greek letter represents the constant ratio of the circumference of any circle to its diameter, approximately equal to 3.14159. One method of deriving this formula, which originated with Archimedes, involves viewing the circle as the limit of a sequence of regular polygons with an increasing number of sides. The area of a regular polygon is half its perimeter multiplied by the distance from its center to its sides, and because the sequence tends to a circle, the corresponding formula–that the area is half the circumference times the radius–namely, , holds for a circle. Terminology Although often referred to as the area of a circle in informal contexts, strictly speaking, the term disk refers to the interior region of the circle, while circle is reserved for the boundary only, which is a curve and covers no area itself. Therefore, the area of a disk is the more precise phrase for the area enclos ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Calculus
Calculus is the mathematics, mathematical study of continuous change, in the same way that geometry is the study of shape, and algebra is the study of generalizations of arithmetic operations. Originally called infinitesimal calculus or "the calculus of infinitesimals", it has two major branches, differential calculus and integral calculus. The former concerns instantaneous Rate of change (mathematics), rates of change, and the slopes of curves, while the latter concerns accumulation of quantities, and areas under or between curves. These two branches are related to each other by the fundamental theorem of calculus. They make use of the fundamental notions of convergence (mathematics), convergence of infinite sequences and Series (mathematics), infinite series to a well-defined limit (mathematics), limit. It is the "mathematical backbone" for dealing with problems where variables change with time or another reference variable. Infinitesimal calculus was formulated separately ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Syracuse, Sicily
Syracuse ( ; ; ) is a historic city on the Italian island of Sicily, the capital of the Italian province of Syracuse. The city is notable for its rich Greek and Roman history, culture, amphitheatres, architecture, and as the birthplace and home of the pre-eminent mathematician and engineer Archimedes. This 2,700-year-old city played a key role in ancient times, when it was one of the major powers of the Mediterranean world. Syracuse is located in the southeast corner of the island of Sicily, next to the Gulf of Syracuse beside the Ionian Sea. It is situated in a drastic rise of land with depths being close to the city offshore although the city itself is generally not so hilly in comparison. The city was founded by Ancient Greek Corinthians and Teneans and became a very powerful city-state. Syracuse was allied with Sparta and Corinth and exerted influence over the entirety of Magna Graecia, of which it was the most important city. Described by Cicero as "the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Mathematical Analysis
Analysis is the branch of mathematics dealing with continuous functions, limit (mathematics), limits, and related theories, such as Derivative, differentiation, Integral, integration, measure (mathematics), measure, infinite sequences, series (mathematics), series, and analytic functions. These theories are usually studied in the context of Real number, real and Complex number, complex numbers and Function (mathematics), functions. Analysis evolved from calculus, which involves the elementary concepts and techniques of analysis. Analysis may be distinguished from geometry; however, it can be applied to any Space (mathematics), space of mathematical objects that has a definition of nearness (a topological space) or specific distances between objects (a metric space). History Ancient Mathematical analysis formally developed in the 17th century during the Scientific Revolution, but many of its ideas can be traced back to earlier mathematicians. Early results in analysis were ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
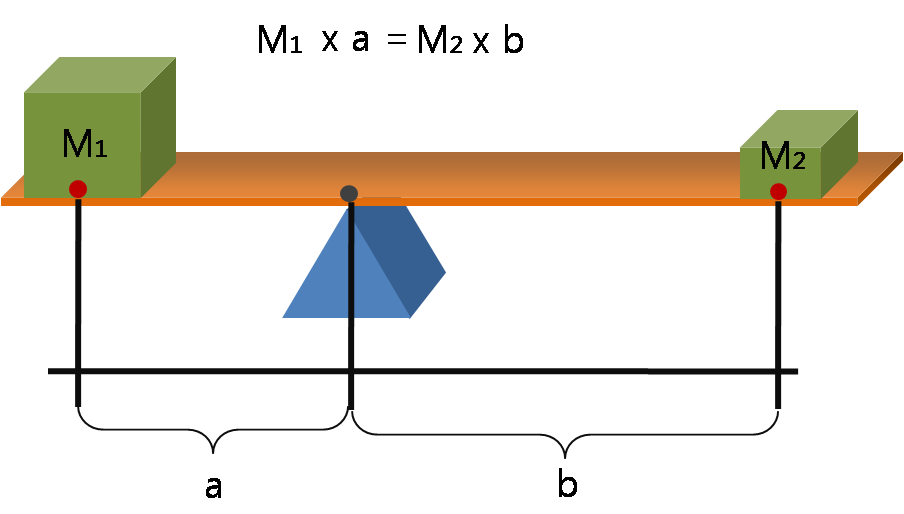
Lever
A lever is a simple machine consisting of a beam (structure), beam or rigid rod pivoted at a fixed hinge, or '':wikt:fulcrum, fulcrum''. A lever is a rigid body capable of rotating on a point on itself. On the basis of the locations of fulcrum, load, and effort, the lever is divided into Lever#Types of levers, three types. It is one of the six simple machines identified by Renaissance scientists. A lever amplifies an input force to provide a greater output force, which is said to provide leverage, which is mechanical advantage gained in the system, equal to the ratio of the output force to the input force. As such, the lever is a mechanical advantage device, trading off force against movement. Etymology The word "lever" entered English language, English around 1300 from . This sprang from the stem of the verb ''lever'', meaning "to raise". The verb, in turn, goes back to , itself from the adjective ''levis'', meaning "light" (as in "not heavy"). The word's primary origin is the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Method Of Exhaustion
The method of exhaustion () is a method of finding the area of a shape by inscribing inside it a sequence of polygons (one at a time) whose areas converge to the area of the containing shape. If the sequence is correctly constructed, the difference in area between the ''n''th polygon and the containing shape will become arbitrarily small as ''n'' becomes large. As this difference becomes arbitrarily small, the possible values for the area of the shape are systematically "exhausted" by the lower bound areas successively established by the sequence members. The method of exhaustion typically required a form of proof by contradiction, known as ''reductio ad absurdum''. This amounts to finding an area of a region by first comparing it to the area of a second region, which can be "exhausted" so that its area becomes arbitrarily close to the true area. The proof involves assuming that the true area is greater than the second area, proving that assertion false, assuming it is less than ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Geometry
Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician who works in the field of geometry is called a ''List of geometers, geometer''. Until the 19th century, geometry was almost exclusively devoted to Euclidean geometry, which includes the notions of point (geometry), point, line (geometry), line, plane (geometry), plane, distance, angle, surface (mathematics), surface, and curve, as fundamental concepts. Originally developed to model the physical world, geometry has applications in almost all sciences, and also in art, architecture, and other activities that are related to graphics. Geometry also has applications in areas of mathematics that are apparently unrelated. For example, methods of algebraic geometry are fundamental in Wiles's proof of Fermat's Last Theorem, Wiles's proof of Fermat's ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |