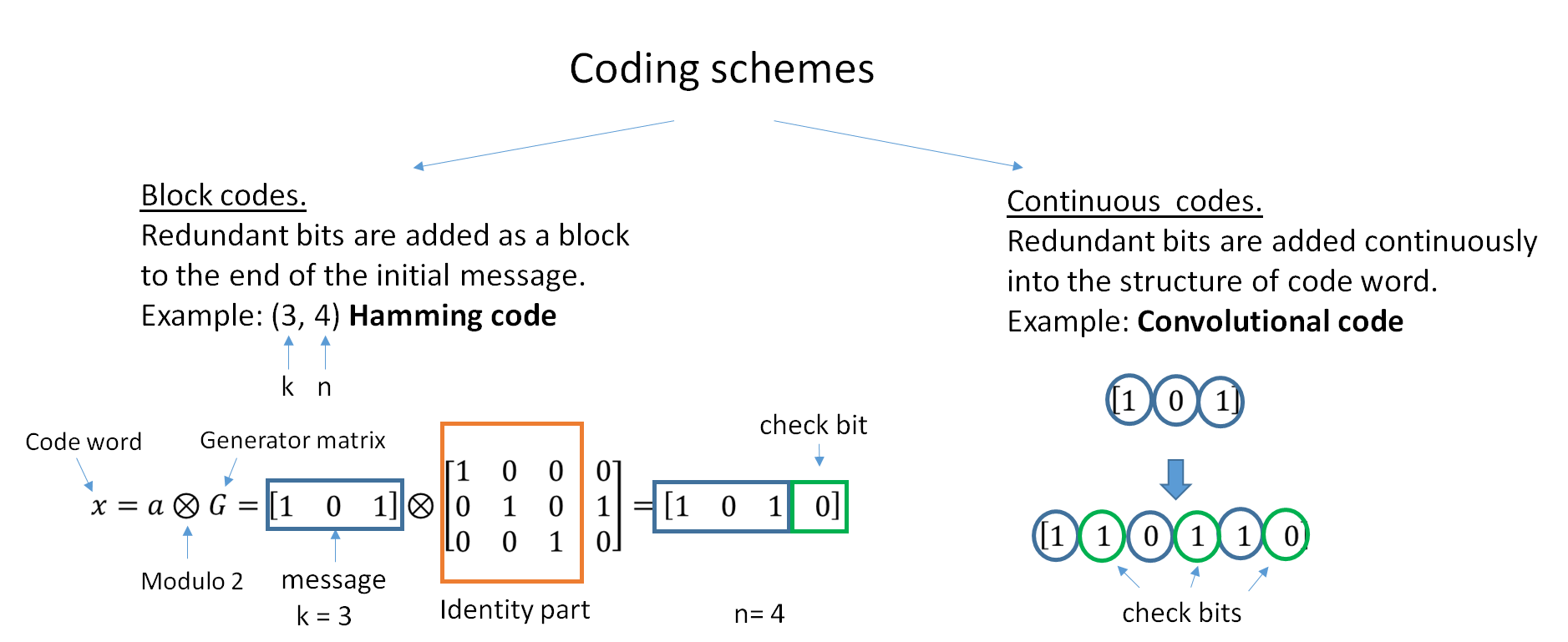
|
AN Codes
AN codes are error-correcting code that are used in arithmetic applications. Arithmetic codes were commonly used in computer processors to ensure the accuracy of its arithmetic operations when electronics were more unreliable. Arithmetic codes help the processor to detect when an error is made and correct it. Without these codes, processors would be unreliable since any errors would go undetected. AN codes are arithmetic codes that are named for the integers A and N that are used to encode and decode the codewords. These codes differ from most other codes in that they use arithmetic weight to maximize the arithmetic distance between codewords as opposed to the hamming weight and hamming distance. The arithmetic distance between two words is a measure of the number of errors made while computing an arithmetic operation. Using the arithmetic distance is necessary since one error in an arithmetic operation can cause a large hamming distance between the received answer and the co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Error-correcting Code
In computing, telecommunication, information theory, and coding theory, an error correction code, sometimes error correcting code, (ECC) is used for controlling errors in data over unreliable or noisy communication channels. The central idea is the sender encodes the message with redundant information in the form of an ECC. The redundancy allows the receiver to detect a limited number of errors that may occur anywhere in the message, and often to correct these errors without retransmission. The American mathematician Richard Hamming pioneered this field in the 1940s and invented the first error-correcting code in 1950: the Hamming (7,4) code. ECC contrasts with error detection in that errors that are encountered can be corrected, not simply detected. The advantage is that a system using ECC does not require a reverse channel to request retransmission of data when an error occurs. The downside is that there is a fixed overhead that is added to the message, thereby requiring a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hamming Weight
The Hamming weight of a string is the number of symbols that are different from the zero-symbol of the alphabet used. It is thus equivalent to the Hamming distance from the all-zero string of the same length. For the most typical case, a string of bits, this is the number of 1's in the string, or the digit sum of the binary representation of a given number and the ''ℓ''₁ norm of a bit vector. In this binary case, it is also called the population count, popcount, sideways sum, or bit summation. History and usage The Hamming weight is named after Richard Hamming although he did not originate the notion. The Hamming weight of binary numbers was already used in 1899 by James W. L. Glaisher to give a formula for the number of odd binomial coefficients in a single row of Pascal's triangle. Irving S. Reed introduced a concept, equivalent to Hamming weight in the binary case, in 1954. Hamming weight is used in several disciplines including information theory, coding theo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hamming Distance
In information theory, the Hamming distance between two strings of equal length is the number of positions at which the corresponding symbols are different. In other words, it measures the minimum number of ''substitutions'' required to change one string into the other, or the minimum number of ''errors'' that could have transformed one string into the other. In a more general context, the Hamming distance is one of several string metrics for measuring the edit distance between two sequences. It is named after the American mathematician Richard Hamming. A major application is in coding theory, more specifically to block codes, in which the equal-length strings are vectors over a finite field. Definition The Hamming distance between two equal-length strings of symbols is the number of positions at which the corresponding symbols are different. Examples The symbols may be letters, bits, or decimal digits, among other possibilities. For example, the Hamming distance betwe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cyclic Code
In coding theory, a cyclic code is a block code, where the circular shifts of each codeword gives another word that belongs to the code. They are error-correcting codes that have algebraic properties that are convenient for efficient error detection and correction. Definition Let \mathcal be a linear code over a finite field (also called '' Galois field'') GF(q) of block length n. \mathcal is called a cyclic code if, for every codeword c=(c_1,\ldots,c_n) from \mathcal, the word (c_n,c_1,\ldots,c_) in GF(q)^n obtained by a cyclic right shift of components is again a codeword. Because one cyclic right shift is equal to n-1 cyclic left shifts, a cyclic code may also be defined via cyclic left shifts. Therefore the linear code \mathcal is cyclic precisely when it is invariant under all cyclic shifts. Cyclic codes have some additional structural constraint on the codes. They are based on Galois fields and because of their structural properties they are very useful for error contro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Non-adjacent Form
The non-adjacent form (NAF) of a number is a unique signed-digit representation, in which non-zero values cannot be adjacent. For example: :(0 1 1 1)2 = 4 + 2 + 1 = 7 :(1 0 −1 1)2 = 8 − 2 + 1 = 7 :(1 −1 1 1)2 = 8 − 4 + 2 + 1 = 7 :(1 0 0 −1)2 = 8 − 1 = 7 All are valid signed-digit representations of 7, but only the final representation, (1 0 0 −1), is in non-adjacent form. The non-adjacent form is also known as "canonical signed digit" representation. Properties NAF assures a unique representation of an integer, but the main benefit of it is that the Hamming weight of the value will be minimal. For regular binary representations of values, half of all bits will be non-zero, on average, but with NAF this drops to only one-third of all digits. This leads to efficient implementations of add/subtract networks (e.g. multiplication by a constant) in hardwired digital signal processing. Obviously, at most half of the digits are non-zero, which was the reason it was int ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Error Detection And Correction
In information theory and coding theory with applications in computer science and telecommunication, error detection and correction (EDAC) or error control are techniques that enable reliable delivery of digital data over unreliable communication channels. Many communication channels are subject to channel noise, and thus errors may be introduced during transmission from the source to a receiver. Error detection techniques allow detecting such errors, while error correction enables reconstruction of the original data in many cases. Definitions ''Error detection'' is the detection of errors caused by noise or other impairments during transmission from the transmitter to the receiver. ''Error correction'' is the detection of errors and reconstruction of the original, error-free data. History In classical antiquity, copyists of the Hebrew Bible were paid for their work according to the number of stichs (lines of verse). As the prose books of the Bible were hardly ever ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Forward Error Correction
In computing, telecommunication, information theory, and coding theory, an error correction code, sometimes error correcting code, (ECC) is used for controlling errors in data over unreliable or noisy communication channels. The central idea is the sender encodes the message with redundant information in the form of an ECC. The redundancy allows the receiver to detect a limited number of errors that may occur anywhere in the message, and often to correct these errors without retransmission. The American mathematician Richard Hamming pioneered this field in the 1940s and invented the first error-correcting code in 1950: the Hamming (7,4) code. ECC contrasts with error detection in that errors that are encountered can be corrected, not simply detected. The advantage is that a system using ECC does not require a reverse channel to request retransmission of data when an error occurs. The downside is that there is a fixed overhead that is added to the message, thereby requiring a hi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |